7 Is Ten Times The Value Of What Number
Breaking News Today
Jun 08, 2025 · 4 min read
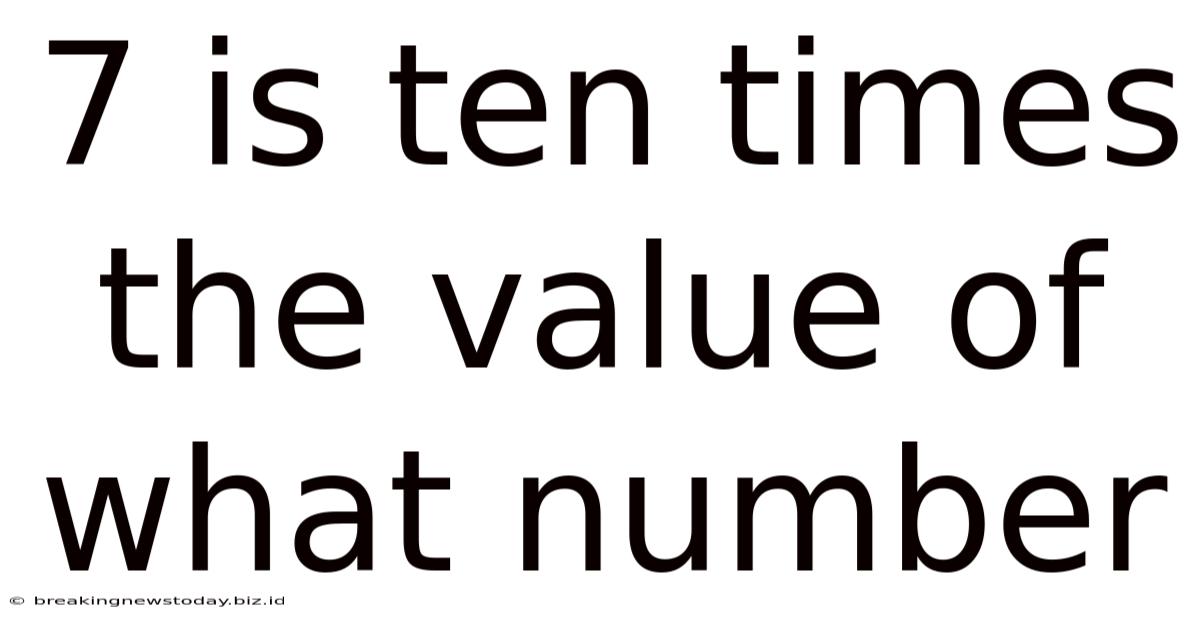
Table of Contents
7 is Ten Times the Value of What Number? Unlocking the Power of Decimal Place Value
Understanding the relationship between numbers is fundamental to mathematics. This seemingly simple question, "7 is ten times the value of what number?", opens a door to a deeper comprehension of place value, decimal systems, and proportional reasoning. This article will not only answer the question directly but will also explore the underlying concepts, providing you with a robust understanding of this mathematical principle.
Deciphering the Question: A Breakdown
The statement "7 is ten times the value of what number?" implies a multiplicative relationship. We're looking for a number that, when multiplied by 10, equals 7. This is a classic example of working backwards from a known product to find an unknown factor.
To solve this, we can represent the problem using an equation:
10 * x = 7
Where 'x' represents the unknown number we're trying to find.
Solving the Equation: Finding the Unknown
To isolate 'x' and find its value, we need to perform the inverse operation of multiplication, which is division. We divide both sides of the equation by 10:
x = 7 / 10
This gives us the answer:
x = 0.7
Therefore, 7 is ten times the value of 0.7.
Understanding Place Value: The Decimal System
The solution, 0.7, highlights the importance of understanding the decimal system's place value. The decimal system is a base-10 system, meaning it's based on powers of 10. Each place to the left of the decimal point represents a power of 10 (ones, tens, hundreds, thousands, etc.), while each place to the right represents a fractional power of 10 (tenths, hundredths, thousandths, etc.).
Visualizing Place Value
Consider the number 7.0. This can be broken down as:
- 7: Represents 7 ones (7 x 10⁰).
- 0: Represents 0 tenths (0 x 10⁻¹).
Now let's look at 0.7:
- 0: Represents 0 ones (0 x 10⁰).
- 7: Represents 7 tenths (7 x 10⁻¹).
Notice the relationship: Moving the decimal point one place to the left is equivalent to dividing by 10. Conversely, moving it one place to the right is equivalent to multiplying by 10.
Expanding the Concept: Exploring Proportions
The problem "7 is ten times the value of what number?" can also be viewed through the lens of proportions. Proportions express the equality of two ratios. We can express the relationship as:
7 / x = 10 / 1
This reads as "7 is to x as 10 is to 1." To solve for x, we can cross-multiply:
7 * 1 = 10 * x
7 = 10x
Dividing both sides by 10 again gives us:
x = 0.7
Applications in Real-World Scenarios
Understanding this concept extends beyond simple mathematical exercises. It has numerous real-world applications:
- Currency Conversion: Converting between currencies often involves multiplying or dividing by exchange rates. Understanding how to adjust values based on these multipliers is crucial.
- Scaling Recipes: When scaling a recipe up or down, you're essentially multiplying or dividing ingredient quantities. Knowing how to adjust values proportionally is essential for successful cooking.
- Unit Conversions: Converting between units of measurement (e.g., meters to centimeters, kilograms to grams) involves multiplication or division by factors of 10. This concept underpins successful conversions.
- Data Analysis: In data analysis, manipulating data often requires scaling or resizing values. Understanding decimal place value and proportional reasoning is essential for accurate interpretations.
- Financial Calculations: Interest calculations, investment growth, and loan repayments all rely on proportional reasoning and manipulating decimal values.
Further Exploration: Extending the Concept
Let's consider variations of the original problem to solidify our understanding:
- "70 is ten times the value of what number?" In this case, the equation becomes 10x = 70, and solving for x gives x = 7. Notice that multiplying 7 by 10 gives 70. The decimal point has effectively shifted one place to the right.
- "0.07 is ten times the value of what number?" Here, the equation becomes 10x = 0.07, and solving for x results in x = 0.007. Again, the decimal point has shifted one place to the left.
These examples demonstrate the consistent relationship between multiplying or dividing by 10 and the movement of the decimal point.
Mastering the Fundamentals: Practice Makes Perfect
To truly internalize the concept, practice solving similar problems. Try varying the initial number (instead of 7) and see how the solution changes. This hands-on practice will reinforce your understanding of place value, decimal operations, and proportional reasoning.
Conclusion: A Foundation for Mathematical Success
The question, "7 is ten times the value of what number?", while seemingly simple, serves as a powerful introduction to crucial mathematical concepts. Understanding place value, decimal operations, and proportional reasoning provides a strong foundation for tackling more complex mathematical problems across various disciplines. By mastering these fundamentals, you equip yourself with valuable skills applicable in numerous real-world scenarios. Consistent practice and a curious approach will unlock your full mathematical potential. Remember, the journey of mathematical understanding is continuous, and each new concept builds upon previous knowledge.
Latest Posts
Latest Posts
-
Rosa Opened A Savings Account At A Bank
Jun 08, 2025
-
What Is Most Important To Consider When Transmitting Organizational Data
Jun 08, 2025
-
True Or False Phishing Is Not Often Responsible For Pii
Jun 08, 2025
-
You Never Have To Worry About Wastewater Becoming Contaminated
Jun 08, 2025
-
Farming Became More Difficult In Iraq In The 1970s Because
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about 7 Is Ten Times The Value Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.