7a - 8 - 12a + 4
Breaking News Today
Jun 05, 2025 · 6 min read
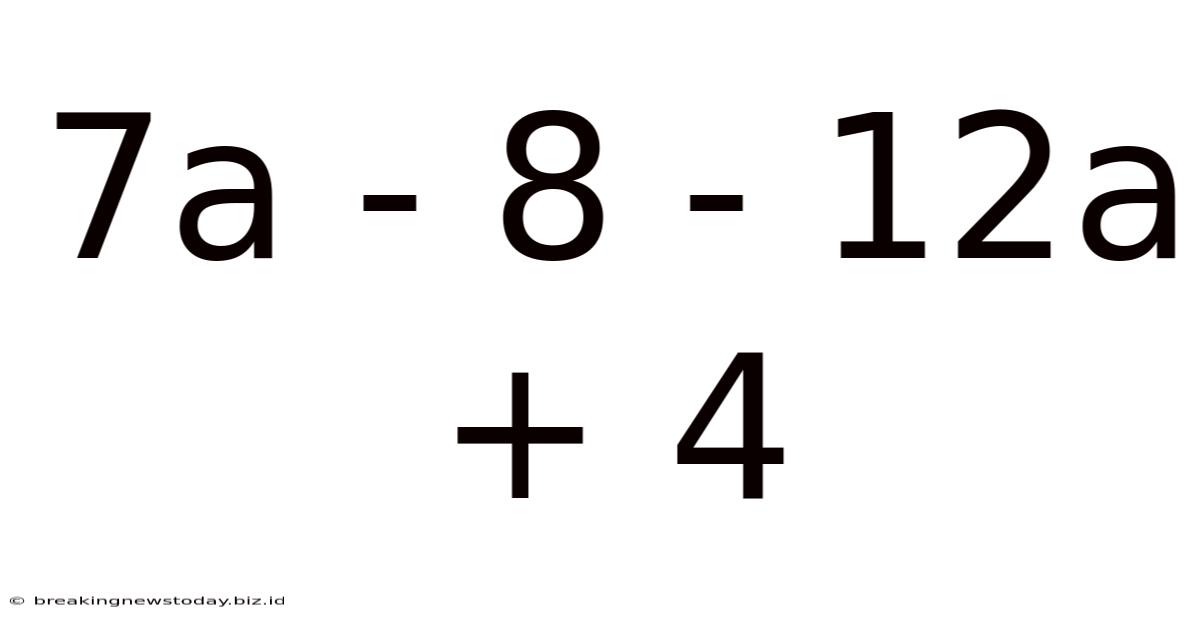
Table of Contents
Unraveling the Mathematical Mystery: A Deep Dive into 7a - 8 - 12a + 4
This seemingly simple algebraic expression, 7a - 8 - 12a + 4, opens doors to a fascinating world of mathematical concepts. While it might appear straightforward at first glance, exploring its various facets reveals a wealth of knowledge applicable to a wide range of mathematical disciplines. This article will comprehensively analyze this expression, covering simplification, solving for 'a', real-world applications, and connections to broader mathematical ideas.
1. Simplifying the Expression: Combining Like Terms
The first step in understanding 7a - 8 - 12a + 4 is simplification. This involves combining like terms, which are terms containing the same variable raised to the same power. In our expression, the like terms are 7a and -12a, and -8 and +4.
Let's break down the simplification process:
-
Combining 'a' terms: 7a - 12a = -5a. This is because subtracting 12a from 7a is equivalent to adding -12a to 7a.
-
Combining constant terms: -8 + 4 = -4. This is straightforward addition of integers.
Therefore, the simplified expression becomes -5a - 4. This simpler form is equivalent to the original expression but is much easier to work with. This process highlights the importance of recognizing and grouping like terms for efficient mathematical manipulation. Mastering this skill is fundamental for solving more complex equations and inequalities.
2. Solving for 'a': Unveiling the Unknown
The simplified expression, -5a - 4, can be used to solve for the value of 'a' given a specific context. This requires setting the expression equal to a certain value, resulting in an equation. Let's explore a few scenarios:
Scenario 1: -5a - 4 = 0
To solve this equation, we need to isolate 'a'. We can do this using inverse operations:
-
Add 4 to both sides: -5a - 4 + 4 = 0 + 4 => -5a = 4
-
Divide both sides by -5: -5a / -5 = 4 / -5 => a = -4/5 or a = -0.8
Scenario 2: -5a - 4 = 11
Again, we isolate 'a' using inverse operations:
-
Add 4 to both sides: -5a - 4 + 4 = 11 + 4 => -5a = 15
-
Divide both sides by -5: -5a / -5 = 15 / -5 => a = -3
These examples demonstrate how the simplified expression can be used to solve for 'a' given different conditions. The ability to manipulate equations and solve for unknowns is a cornerstone of algebra and is widely applied in various fields.
3. Real-World Applications: Bringing the Math to Life
While the expression 7a - 8 - 12a + 4 might seem abstract, it has practical applications in numerous real-world scenarios. Let's explore a couple of examples:
Example 1: Profit Calculation
Imagine a small business selling handmade crafts. Let's say:
- 'a' represents the number of crafts sold.
- 7a represents the revenue from selling the crafts at $7 each.
- 12a represents the cost of materials at $12 per craft.
- 8 represents fixed costs (rent, utilities).
- 4 represents additional income from online sales.
The expression 7a - 8 - 12a + 4 would represent the business's profit. Simplifying the expression to -5a - 4 shows that for each craft sold, the business loses $5, and the fixed costs and additional income lead to a net loss of $4. This simple model helps the business owner understand their financial situation and make necessary adjustments.
Example 2: Temperature Change
Consider a scenario where 'a' represents the number of hours. 7a could represent a temperature increase of 7 degrees Celsius per hour, while -12a represents a temperature decrease due to cooling. The constants, -8 and 4, could represent initial temperature and a sudden heat surge. The resulting expression, 7a - 8 - 12a + 4, shows the net temperature change over 'a' hours. Simplifying to -5a - 4 allows for easier calculation of the temperature at any given time.
4. Expanding Mathematical Horizons: Connections to Broader Concepts
This seemingly simple algebraic expression opens doors to various advanced mathematical concepts:
-
Linear Equations: The simplified expression, -5a - 4, represents a linear equation. Linear equations are fundamental in algebra and form the basis for understanding linear relationships between variables. They are used extensively in modeling various phenomena across different fields.
-
Functions: The expression can be considered a function of 'a', denoted as f(a) = -5a - 4. Functions are crucial in calculus and analysis, allowing us to study relationships between inputs and outputs.
-
Graphing: The linear equation can be easily graphed, providing a visual representation of the relationship between 'a' and the value of the expression. The graph will be a straight line with a slope of -5 and a y-intercept of -4. Graphing helps visualize the behavior of the function and understand its properties.
-
Inequalities: The expression can be used to create inequalities. For instance, -5a - 4 > 0 allows us to find the values of 'a' where the expression is greater than zero. Solving inequalities is an important skill used in optimization problems and decision-making processes.
-
Systems of Equations: The expression could be part of a larger system of equations, involving other variables and equations. Solving such systems requires utilizing techniques like substitution or elimination and is crucial in many areas, like solving simultaneous equations in physics and engineering.
5. Beyond the Basics: Further Exploration
To further delve into the mathematical richness of this expression, consider these advanced exercises:
-
Finding the roots: Setting the expression equal to zero (-5a - 4 = 0) and solving for 'a' helps find the 'root' or the value of 'a' where the expression equals zero. This concept is central to finding solutions to equations and analyzing the behavior of functions.
-
Analyzing the slope and intercept: When graphed, the expression represents a straight line. The slope (-5) indicates the rate of change, and the y-intercept (-4) represents the value of the expression when 'a' is zero. Understanding these parameters helps in interpreting the graphical representation of the function.
-
Exploring different values of 'a': Substitute different values of 'a' (positive, negative, zero) into the expression to observe the resulting values and analyze the relationship between 'a' and the output. This hands-on exploration solidifies understanding and reveals the nature of the function.
6. Conclusion: A Foundation for Mathematical Growth
The seemingly simple expression 7a - 8 - 12a + 4 offers a wealth of mathematical insights. From simplifying expressions and solving equations to understanding real-world applications and exploring advanced concepts like functions and inequalities, this seemingly basic algebraic expression serves as a solid foundation for deeper mathematical learning. Mastering these fundamental concepts will unlock the doors to more complex mathematical challenges and applications across various disciplines. The journey from simplification to advanced analysis showcases the power of mathematical reasoning and problem-solving. Remember that consistent practice and a curious approach to mathematical concepts are keys to unlocking further mathematical understanding and success.
7. Keywords for SEO Optimization:
algebraic expression, simplify, combine like terms, solve for a, linear equation, real-world applications, functions, graphing, inequalities, systems of equations, mathematical concepts, 7a - 8 - 12a + 4, algebra, mathematics, problem-solving, equation solving, mathematical analysis, linear function.
Latest Posts
Latest Posts
-
Each Area Of The Face Is Shaved Systematically And
Jun 06, 2025
-
The Difference Of Eleven And Four Times Five
Jun 06, 2025
-
10 6 Exponential Growth And Decay Answer Key
Jun 06, 2025
-
Which Type Of Conflict Is Presented In This Excerpt
Jun 06, 2025
-
Match Each Dts Role With Its Primary Responsibility
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about 7a - 8 - 12a + 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.