8.25 Of What Number Is $7.26
Breaking News Today
Jun 06, 2025 · 4 min read
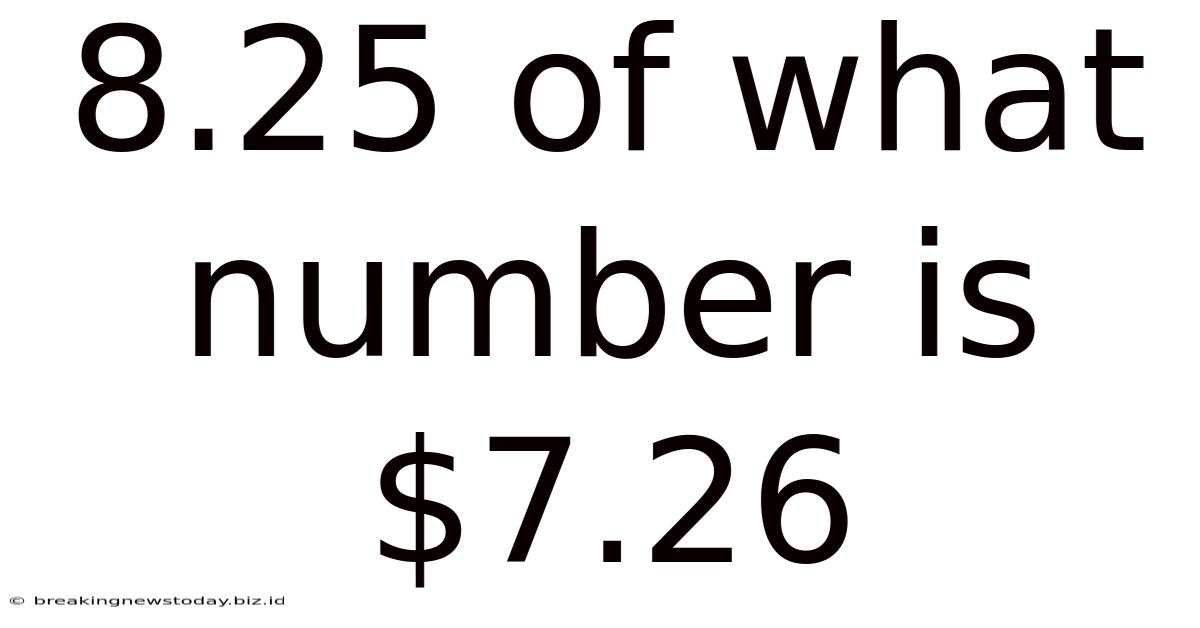
Table of Contents
8.25% of What Number is $7.26? A Comprehensive Guide to Percentage Calculations
Finding the base number when you know a percentage and its value is a fundamental concept in mathematics with broad applications in various fields, from finance and business to everyday life. This article dives deep into solving the problem: "8.25% of what number is $7.26?" We'll explore multiple methods to arrive at the solution, understand the underlying principles, and discuss practical applications. We’ll also cover important related concepts to solidify your understanding of percentage calculations.
Understanding the Problem: Deconstructing the Question
The question, "8.25% of what number is $7.26?" asks us to find the original whole number (often called the base) from which 8.25% represents $7.26. This is a common type of percentage problem, requiring us to work backward from the percentage and its corresponding value to find the base. This is different from calculating a percentage of a known number.
Method 1: Using the Percentage Formula
The most direct way to solve this problem is using the basic percentage formula:
Percentage = (Part / Whole) x 100
In our case:
- Percentage: 8.25%
- Part: $7.26
- Whole: This is what we need to find (let's represent it with 'x')
Substituting these values into the formula, we get:
8.25 = (7.26 / x) x 100
Now, we solve for 'x':
- Divide both sides by 100: 0.0825 = 7.26 / x
- Multiply both sides by x: 0.0825x = 7.26
- Divide both sides by 0.0825: x = 7.26 / 0.0825
Therefore:
x ≈ 88
Therefore, 8.25% of 88 is approximately $7.26. Note that we use "approximately" because the calculation involves a decimal number, and slight rounding errors might occur.
Method 2: Using Proportions
Another effective approach involves setting up a proportion. We can express the problem as a ratio:
8.25 / 100 = 7.26 / x
This proportion states that the ratio of the percentage to 100 is equal to the ratio of the part to the whole. Cross-multiplying to solve for 'x':
8.25x = 726
x = 726 / 8.25
x ≈ 88
Again, we arrive at the solution: 88 is the number.
Method 3: Algebraic Approach
We can directly translate the problem into an algebraic equation:
0.0825x = 7.26
This equation represents the problem: 8.25% (or 0.0825 as a decimal) of an unknown number (x) equals $7.26. Solving for x:
x = 7.26 / 0.0825
x ≈ 88
Understanding Percentage Increase and Decrease
Understanding percentages extends beyond simple calculations. It's crucial to grasp percentage increases and decreases. Let's say we have a starting value and it increases by a certain percentage. The formula for calculating the new value is:
New Value = Original Value + (Original Value x Percentage Increase)
Conversely, for a percentage decrease:
New Value = Original Value - (Original Value x Percentage Decrease)
These formulas are particularly relevant in financial applications, such as calculating interest, discounts, tax, and profit margins.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in daily life and various professional fields:
- Finance: Calculating interest rates, loan repayments, investment returns, and tax rates.
- Business: Determining profit margins, discounts, sales growth, and market share.
- Science: Representing data in graphs, charts, and statistical analyses.
- Everyday Life: Calculating tips, discounts at stores, and understanding sales tax.
Advanced Percentage Problems: Compound Interest
A more complex application involves compound interest. Unlike simple interest, where interest is calculated only on the principal amount, compound interest accrues on both the principal and accumulated interest. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Error Handling and Precision
When working with percentages, especially involving decimal numbers, it's essential to consider potential rounding errors. Using a calculator or spreadsheet software with high precision can minimize these errors. It's always good practice to carry extra decimal places during calculations and round only the final result to the desired level of accuracy.
Tips for Solving Percentage Problems
- Convert percentages to decimals: Divide the percentage by 100.
- Identify the known and unknown values: Determine what information is given and what needs to be calculated.
- Choose the appropriate formula: Select the correct formula based on the problem type.
- Check your work: Verify the solution by substituting the calculated value back into the original problem.
- Use a calculator or spreadsheet: Utilizing tools can improve accuracy and speed.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill applicable across various domains. This article provided multiple approaches to solving the problem of finding the base number, emphasizing the importance of understanding the underlying principles and employing different methods to ensure accuracy. By practicing these methods and understanding the related concepts, you'll improve your problem-solving skills and enhance your ability to analyze and interpret data effectively. Remember, the key is to understand the core concepts, choose the most suitable method for the problem, and always double-check your work. With practice, you'll become proficient in handling percentage calculations with confidence.
Latest Posts
Latest Posts
-
Which Statement Correctly Compares Sound And Light Waves
Jun 07, 2025
-
3 01 Quiz Atomic Number And The Periodic Law
Jun 07, 2025
-
Which Expression Is Equivalent To Y 48
Jun 07, 2025
-
To Effectively Search The Total Traffic Scene
Jun 07, 2025
-
Unit 4 Congruent Triangles Quiz 4 1 Answer Key
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 8.25 Of What Number Is $7.26 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.