8 Less Than 3 Times X
Breaking News Today
Jun 05, 2025 · 6 min read
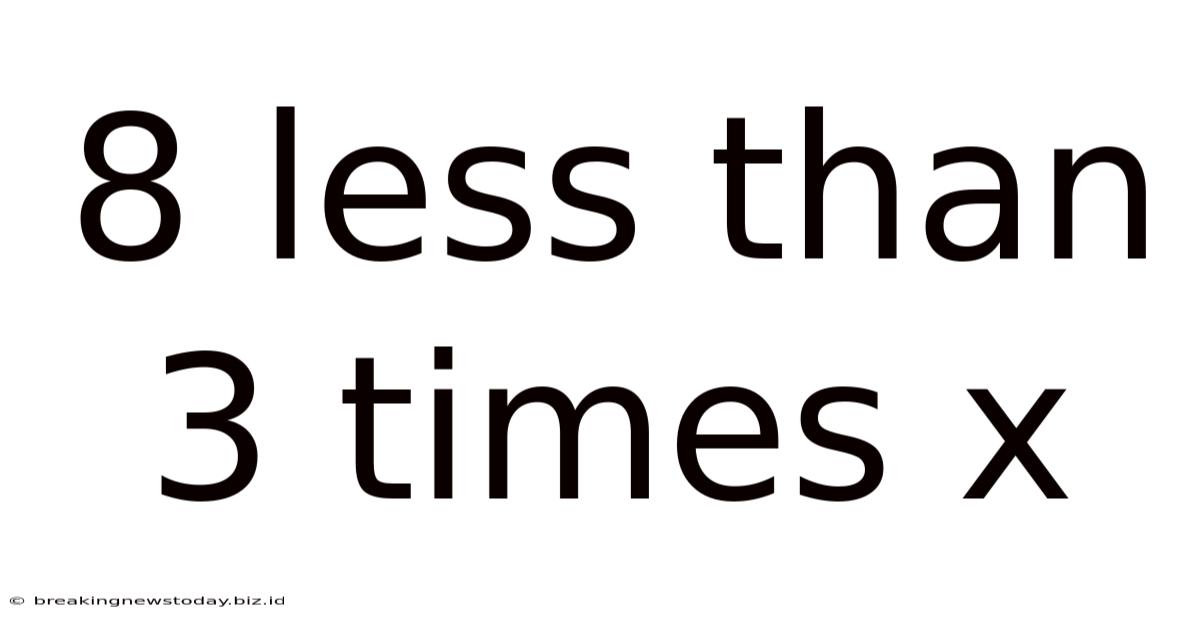
Table of Contents
8 Less Than 3 Times x: A Comprehensive Exploration of Algebraic Expressions
The seemingly simple phrase "8 less than 3 times x" hides a world of mathematical possibilities. This seemingly straightforward statement encapsulates fundamental algebraic concepts, providing a springboard for understanding more complex equations and problem-solving strategies. This article delves deep into the meaning, representation, and applications of this expression, exploring its nuances and demonstrating its versatility in various mathematical contexts.
Understanding the Expression: "8 Less Than 3 Times x"
At its core, the phrase "8 less than 3 times x" describes an algebraic expression. Let's break it down step-by-step:
-
"3 times x": This translates directly to the algebraic term 3x. 'x' represents an unknown variable, and '3' is the coefficient, indicating multiplication.
-
"8 less than": This signifies subtraction. We are taking 8 away from the result of "3 times x".
Therefore, the complete algebraic representation of "8 less than 3 times x" is 3x - 8.
Representing the Expression Visually
Visualizing mathematical concepts can significantly aid understanding. Let's explore ways to visually represent "3x - 8":
1. Number Line Representation:
Imagine a number line. '3x' represents a point on the line whose position depends on the value of 'x'. Subtracting 8 means moving 8 units to the left of that point. This visual helps understand the effect of subtracting 8 from the variable term.
2. Bar Model Representation:
A bar model can effectively illustrate the expression. One bar represents '3x', and another bar, representing 8, is subtracted from it. This provides a concrete visual of the subtraction process.
3. Area Model Representation:
If 'x' represents a length, then '3x' can be visualized as a rectangle with one side of length 'x' and the other side of length 3. Subtracting 8 could be represented by removing a smaller rectangle with an area of 8 from the larger rectangle.
These visual representations offer alternative pathways to understanding the algebraic expression, making it more accessible to learners of all levels.
Manipulating the Expression: Solving for x
The true power of an algebraic expression lies in its ability to be manipulated to solve for the unknown variable, 'x'. This often involves setting the expression equal to a specific value and employing algebraic techniques.
Let's consider an example: If 3x - 8 = 10, what is the value of x?
To solve this, we use the following steps:
-
Add 8 to both sides: This isolates the term with 'x'. The equation becomes 3x = 18.
-
Divide both sides by 3: This solves for 'x'. The result is x = 6.
Therefore, if the expression "8 less than 3 times x" equals 10, then x equals 6.
This simple example highlights the process of solving for a variable within an algebraic expression. More complex equations may involve multiple variables, parentheses, and other operations, but the core principles remain the same – maintaining balance and systematically isolating the target variable.
Real-World Applications of "3x - 8"
The expression "3x - 8" isn't just a theoretical construct; it has practical applications in numerous real-world scenarios:
1. Calculating Profits:
Imagine a small business selling handmade crafts. Each craft sells for $3, and the business has fixed costs of $8. The expression "3x - 8" represents the profit, where 'x' is the number of crafts sold. This allows the business owner to quickly calculate profit based on the number of items sold.
2. Determining Discounts:
A store might offer a discount of $8 off items costing 3 times a base price. If 'x' represents the base price, the final cost of an item would be represented by "3x - 8".
3. Modeling Temperature Changes:
Imagine a situation where the temperature increases by 3 degrees every hour ('3x'), but starts 8 degrees below zero ('-8'). The expression "3x - 8" could model the temperature ('x' representing the number of hours).
4. Calculating Travel Distance:
Suppose a car travels at a speed of 3 times its initial speed ('x'), but loses 8 kilometers due to a detour. The total distance covered could be represented by "3x - 8", with 'x' representing the initial speed.
These examples showcase the versatility of the expression "3x - 8" in modeling various real-world situations, making it a valuable tool in applied mathematics.
Expanding the Concept: More Complex Expressions
While "3x - 8" is a relatively simple expression, it serves as a building block for understanding more intricate algebraic expressions. Let's explore how this foundational understanding can be expanded:
1. Adding More Terms:
The expression could be expanded to include additional terms, such as "3x - 8 + 5y," introducing another variable, 'y'. Solving for either 'x' or 'y' would then require additional information in the form of another equation.
2. Introducing Exponents:
Adding exponents increases the complexity, such as "3x² - 8". This introduces quadratic equations, requiring different solution methods compared to linear equations.
3. Incorporating Parentheses:
Parentheses introduce order of operations, altering the sequence of calculations. For example, "3(x - 2) - 8" requires first simplifying the expression inside the parentheses before proceeding with other operations.
4. Combining Expressions:
Multiple expressions can be combined to form complex equations. For instance, "3x - 8 = 2x + 5" requires manipulating both sides of the equation to isolate 'x' and find the solution.
By building upon the foundational understanding of "3x - 8," one can progressively tackle more complex algebraic expressions and equations.
The Importance of Mastering Algebraic Expressions
Mastering algebraic expressions like "3x - 8" is crucial for success in mathematics and numerous related fields. It forms the bedrock for:
-
Solving Equations: The ability to manipulate and solve equations is paramount in various mathematical and scientific disciplines.
-
Problem Solving: Many real-world problems can be modeled and solved using algebraic expressions and equations.
-
Data Analysis: Understanding algebraic expressions is essential for interpreting and analyzing data.
-
Higher-Level Mathematics: Algebraic expressions are fundamental to calculus, linear algebra, and other advanced mathematical concepts.
Therefore, a thorough understanding of this seemingly simple expression is an investment in future mathematical proficiency and problem-solving skills.
Conclusion: From Simple Phrase to Powerful Tool
The phrase "8 less than 3 times x," initially appearing simple, reveals itself to be a gateway to a vast realm of mathematical concepts. Its exploration unveils the beauty and power of algebraic expressions, highlighting their importance in both theoretical mathematics and practical applications. By mastering the manipulation and application of such expressions, we equip ourselves with invaluable tools for problem-solving and understanding the world around us. The journey from a simple phrase to a powerful mathematical tool underscores the profound interconnectedness within the field of mathematics and its significance in various aspects of life.
Latest Posts
Latest Posts
-
Which Two Statements Are True About All Generators
Jun 06, 2025
-
A Food Handler Needs More Lettuce For Preparing Salads
Jun 06, 2025
-
Which Three Statements About The Gilded Age Are True
Jun 06, 2025
-
What Event Do Both Excerpts Describe
Jun 06, 2025
-
Which Of The Following Best Describes A Data Scientist
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about 8 Less Than 3 Times X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.