8 Thousandths 6 Ones 8 Thousandths
Breaking News Today
Jun 02, 2025 · 5 min read
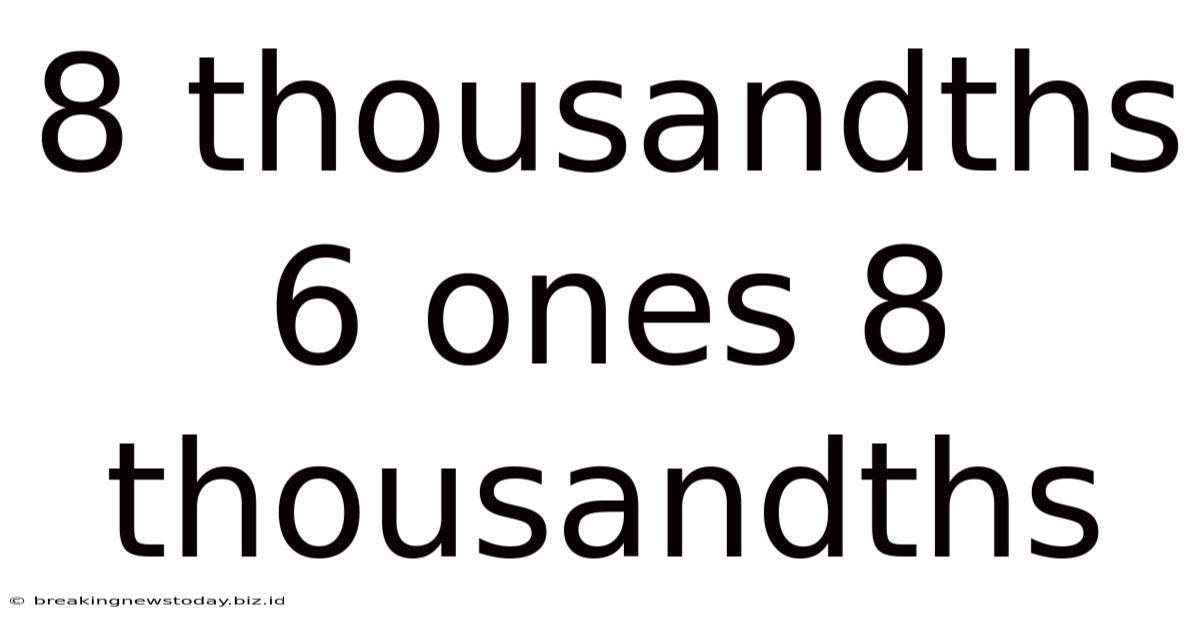
Table of Contents
Decoding 8 Thousandths, 6 Ones, and 8 Thousandths: A Deep Dive into Place Value and Number Representation
Understanding numbers is fundamental to mathematics and everyday life. This article delves into the seemingly simple expression "8 thousandths, 6 ones, and 8 thousandths," exploring its meaning, representation in different forms, and its implications in various mathematical contexts. We'll unpack the concept of place value, the significance of decimal notation, and how this specific numerical combination can be applied to real-world scenarios. We'll also discuss related concepts like rounding, significant figures, and scientific notation, further enriching your understanding of number representation.
Understanding Place Value: The Foundation of Number Systems
Before we analyze "8 thousandths, 6 ones, and 8 thousandths," let's establish a solid understanding of place value. Place value is the principle that the position of a digit in a number determines its value. Each position represents a power of 10. Consider the number 1234:
- 4 is in the ones place (10<sup>0</sup> = 1), representing 4 x 1 = 4
- 3 is in the tens place (10<sup>1</sup> = 10), representing 3 x 10 = 30
- 2 is in the hundreds place (10<sup>2</sup> = 100), representing 2 x 100 = 200
- 1 is in the thousands place (10<sup>3</sup> = 1000), representing 1 x 1000 = 1000
Adding these values together (4 + 30 + 200 + 1000) gives us the total value of the number 1234. This principle extends to numbers with decimal places, which we'll explore next.
Decimals and Place Value: Extending the System
Decimal numbers extend the place value system to represent values less than one. The decimal point separates the whole number part from the fractional part. Positions to the right of the decimal point represent negative powers of 10:
- 10<sup>-1</sup> = 0.1 (tenths)
- 10<sup>-2</sup> = 0.01 (hundredths)
- 10<sup>-3</sup> = 0.001 (thousandths)
- 10<sup>-4</sup> = 0.0001 (ten-thousandths) and so on.
Representing "8 thousandths, 6 ones, and 8 thousandths"
Now, let's dissect the phrase "8 thousandths, 6 ones, and 8 thousandths." This describes a number composed of three distinct parts:
- 6 ones: This represents the whole number part, simply 6.
- 8 thousandths: This represents 8 x 0.001 = 0.008
- 8 thousandths: This is another 8 x 0.001 = 0.008
To combine these, we add them together: 6 + 0.008 + 0.008 = 6.016
Therefore, "8 thousandths, 6 ones, and 8 thousandths" is equivalent to the decimal number 6.016.
Alternative Representations
While 6.016 is the most straightforward representation, we can also explore other ways to express this number:
-
Fraction: The decimal 6.016 can be expressed as a fraction. To do this, we first write it as a fraction with a denominator of 1000 (since the last digit is in the thousandths place): 6016/1000. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 4: 1504/250. Further simplification isn't possible without resorting to decimals.
-
Expanded Form: This shows the value of each digit explicitly: (6 x 1) + (0 x 0.1) + (1 x 0.01) + (6 x 0.001)
-
Scientific Notation: For extremely large or small numbers, scientific notation is preferred. In this case, 6.016 is relatively small, so scientific notation isn't strictly necessary, but it can be expressed as 6.016 x 10<sup>0</sup>.
Real-World Applications
Understanding numbers like 6.016 has practical implications across various fields:
-
Finance: Dealing with monetary values often involves decimals to the hundredths (cents), but precision to the thousandths might be required in situations like high-frequency trading or complex financial calculations involving interest rates or currency exchange.
-
Engineering: Engineers often work with extremely precise measurements and calculations. The thousandths place can be crucial in ensuring accuracy and safety in projects like bridge construction or aircraft design.
-
Science: Scientific measurements, especially in chemistry and physics, frequently involve decimal values with several decimal places to accurately represent experimental data.
-
Data Analysis: In data analysis, understanding the precision of numerical data is critical for drawing accurate conclusions. The number of decimal places retained impacts statistical significance and interpretation.
Rounding and Significant Figures
Rounding and significant figures are important concepts related to representing numbers with appropriate precision.
-
Rounding: Rounding simplifies a number by reducing the number of decimal places. For example, rounding 6.016 to one decimal place gives 6.0, while rounding to two decimal places gives 6.02. The choice of rounding depends on the required level of accuracy.
-
Significant Figures: Significant figures represent the number of digits in a number that are reliably known. For example, 6.016 has four significant figures. Using fewer significant figures can introduce error into calculations, whereas using an excessive number of significant figures often implies a level of precision not actually present.
Expanding Knowledge: Further Exploration
This article provides a foundational understanding of place value, decimal representation, and the interpretation of numbers like "8 thousandths, 6 ones, and 8 thousandths." To expand your knowledge, consider exploring these related topics:
-
Different Number Systems: Explore number systems beyond the base-10 decimal system, such as binary (base-2) and hexadecimal (base-16) systems.
-
Error Analysis: Learn about different types of errors (rounding, truncation, measurement errors) that can occur when working with numbers and how to minimize their impact.
-
Number Theory: Delve deeper into the mathematical properties of numbers, exploring concepts like prime numbers, composite numbers, and divisibility rules.
-
Advanced Mathematical Operations: Apply your understanding of place value and decimal representation to more advanced mathematical operations like calculus and linear algebra.
By mastering the fundamentals of place value and decimal representation, you lay the groundwork for a strong understanding of mathematics and its many practical applications. This seemingly simple phrase, "8 thousandths, 6 ones, and 8 thousandths," highlights the importance of careful consideration of numerical representation and its implications in various contexts. Through continued learning and exploration, you can enhance your mathematical skills and apply this knowledge to real-world problems.
Latest Posts
Latest Posts
-
10982 Rounded To The Nearest Ten Thousand
Jun 04, 2025
-
1 2 Mathematical Literacy And Vocabulary
Jun 04, 2025
-
While Files Have Slanting Parallel Rows Of Teeth A Rasp
Jun 04, 2025
-
Based On The Excerpt Readers Can Conclude That Odysseus
Jun 04, 2025
-
What Statement Best Describes The Space Around A Sculpture
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about 8 Thousandths 6 Ones 8 Thousandths . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.