8x10-3 Is How Many Times As Great As 4x10-6
Breaking News Today
Jun 04, 2025 · 5 min read
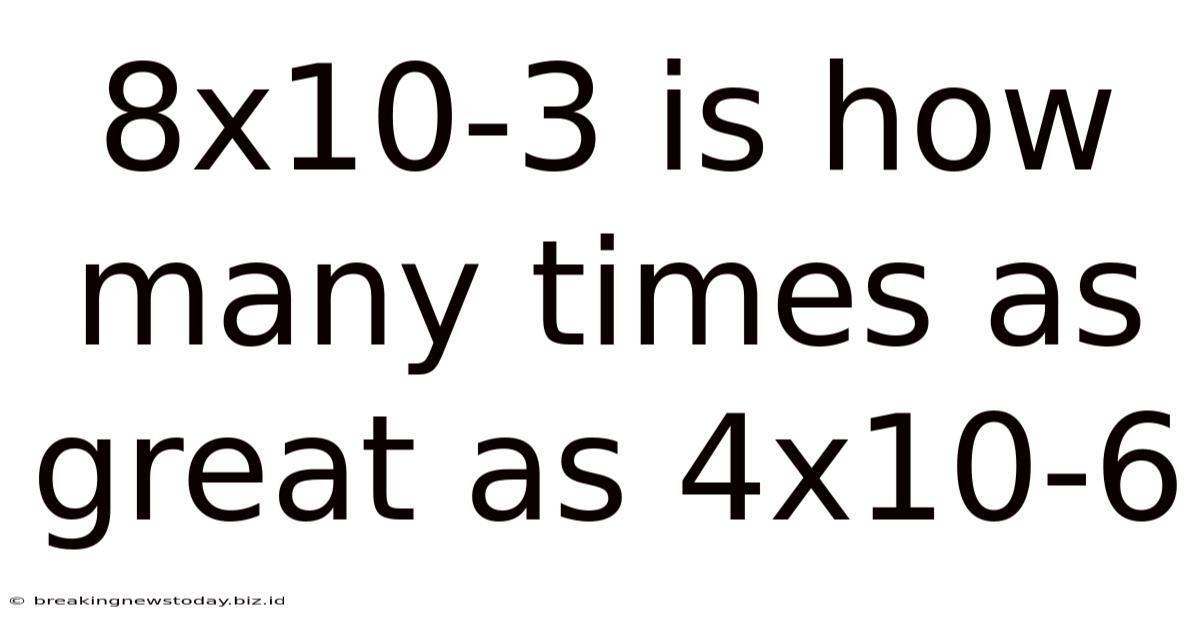
Table of Contents
8x10⁻³ is How Many Times as Great as 4x10⁻⁶? A Deep Dive into Scientific Notation and Order of Magnitude
This seemingly simple question – "8x10⁻³ is how many times as great as 4x10⁻⁶?" – opens a door to a fundamental concept in mathematics and science: scientific notation and understanding orders of magnitude. This article will not only answer the question but provide a comprehensive explanation, exploring the underlying principles and demonstrating practical applications. We'll delve into the mechanics of comparing numbers in scientific notation, offer various approaches to solving the problem, and extend the concepts to broader contexts.
Understanding Scientific Notation
Scientific notation is a standardized way of writing very large or very small numbers. It expresses a number as a product of a coefficient (a number between 1 and 10) and a power of 10. This makes it easier to handle and compare numbers that differ vastly in scale. For instance:
- 1,000,000 can be written as 1 x 10⁶ (10 to the power of 6).
- 0.000001 can be written as 1 x 10⁻⁶ (10 to the power of -6).
The exponent indicates the order of magnitude—the power of 10 that represents the scale of the number. A larger exponent means a larger number.
Comparing Numbers in Scientific Notation
To compare two numbers expressed in scientific notation, we can follow these steps:
-
Examine the exponents: The number with the larger exponent is the greater number. If the exponents are the same, compare the coefficients.
-
Divide to find the ratio: To determine how many times greater one number is than another, we divide the larger number by the smaller number. This will give us the ratio.
Solving the Problem: 8x10⁻³ vs 4x10⁻⁶
Now, let's tackle our original problem: How many times greater is 8x10⁻³ than 4x10⁻⁶?
Method 1: Direct Division
The most straightforward approach is to divide 8x10⁻³ by 4x10⁻⁶:
(8 x 10⁻³) / (4 x 10⁻⁶) = (8/4) x (10⁻³/10⁻⁶) = 2 x 10⁻³⁻⁻⁶ = 2 x 10³ = 2000
Therefore, 8x10⁻³ is 2000 times greater than 4x10⁻⁶.
Method 2: Adjusting Exponents
We can also simplify the calculation by adjusting the exponents to make the base 10 terms equal before dividing:
First, we can rewrite 8 x 10⁻³ as 8000 x 10⁻⁶. This is achieved by multiplying the coefficient by 10³ (to account for the difference in the exponents) and dividing the power of 10 by 10³ to preserve the original value. Now we have:
(8000 x 10⁻⁶) / (4 x 10⁻⁶) = 8000/4 = 2000
Again, we find that 8x10⁻³ is 2000 times greater than 4x10⁻⁶.
Method 3: Understanding Orders of Magnitude
Looking at the exponents directly provides a quick estimate. The difference in the exponents (-3) - (-6) = 3 indicates that 8 x 10⁻³ is 10³ (or 1000) times greater than 4 x 10⁻⁶. Then, we account for the difference in coefficients (8/4 = 2). Combining these, we get 2 x 10³ = 2000.
Applications in Science and Engineering
Understanding orders of magnitude and scientific notation is crucial in many scientific and engineering fields. Here are some examples:
-
Physics: Comparing the mass of an electron (approximately 9.11 x 10⁻³¹ kg) to the mass of the Earth (approximately 5.97 x 10²⁴ kg) requires scientific notation to manage the extreme difference in scale.
-
Chemistry: Working with molar masses of different elements and molecules often involves numbers in scientific notation. Determining the relative abundance of different isotopes necessitates these calculations.
-
Astronomy: Measuring distances between celestial objects, the size of stars, or the age of the universe necessitates the use of scientific notation due to the colossal numbers involved.
-
Computer Science: In computer science, dealing with large datasets, processing speeds, and memory capacities often requires the use of scientific notation.
Extending the Concept: Real-World Examples
Let's consider some real-world scenarios that illustrate the importance of understanding orders of magnitude:
Scenario 1: Comparing National Budgets
Imagine comparing the annual budget of a small country (e.g., $10 billion) with that of a large, developed nation (e.g., $5 trillion). Using scientific notation ($10 x 10⁹ vs $5 x 10¹²), we can easily see the larger nation's budget is 500 times greater.
Scenario 2: Microscopic vs Macroscopic Scales
Consider the size of a bacterium (approximately 1 x 10⁻⁶ meters) compared to the height of a human (approximately 2 meters). The height of a human is approximately 2 x 10⁶ times greater than the size of a bacterium.
Scenario 3: Data Storage
Comparing the storage capacity of a typical flash drive (e.g., 128 GB or approximately 1.28 x 10¹¹ bytes) to a large data center (which might hold petabytes or 10¹⁵ bytes of data) showcases the differences in storage capabilities using scientific notation.
Conclusion: Mastering Scientific Notation for Numerical Proficiency
The ability to work comfortably with scientific notation is fundamental to success in many fields that deal with quantitative data. Understanding how to compare numbers expressed in this format, as demonstrated by our analysis of "8x10⁻³ is how many times as great as 4x10⁻⁶?", is essential. By mastering these techniques, you can effectively analyze and interpret data, making informed decisions and advancing your problem-solving skills across various disciplines. The seemingly simple calculation we've explored unlocks a deeper understanding of scale, magnitude, and numerical representation—a critical aspect of quantitative reasoning. Remember to always break down complex problems into manageable steps, utilizing different methods to cross-verify your results for better accuracy and comprehension.
Latest Posts
Latest Posts
-
300 Is 10 Times As Much As
Jun 06, 2025
-
What Name Best Describes This Shape
Jun 06, 2025
-
A Year Ago Shani Opened Her Own Computer Software Company
Jun 06, 2025
-
Which Statements Are True About Triangle Qrs Select Three Options
Jun 06, 2025
-
Which Expression Is Missing From The Proof
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about 8x10-3 Is How Many Times As Great As 4x10-6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.