9 Less Than Six Times A Number
Breaking News Today
Jun 03, 2025 · 5 min read
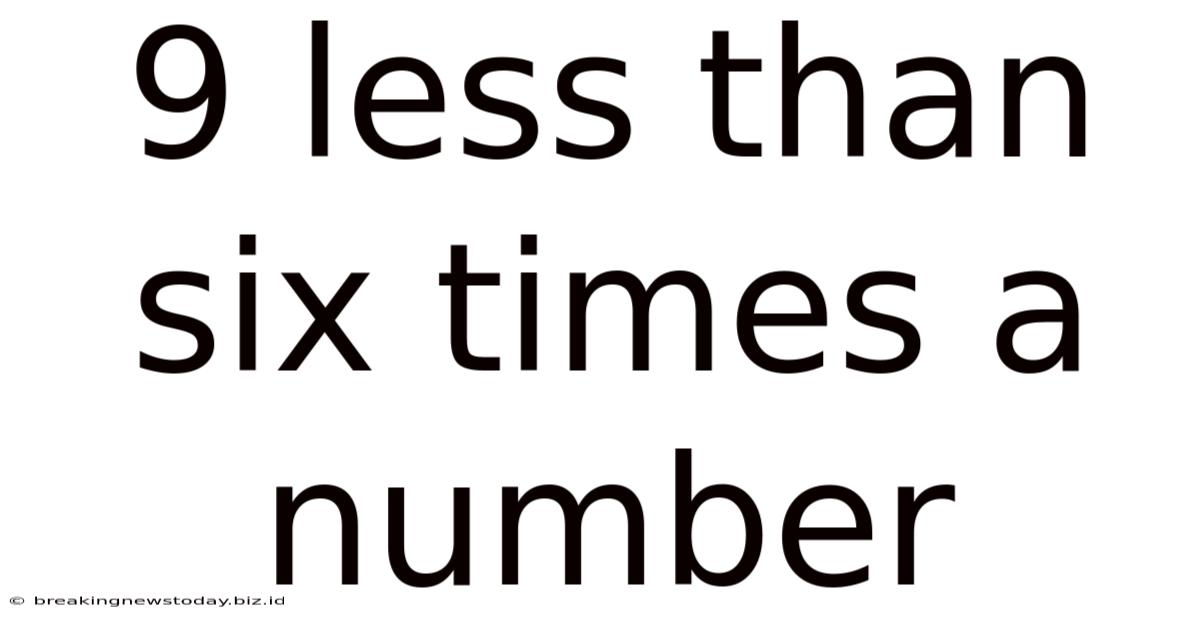
Table of Contents
9 Less Than Six Times a Number: A Deep Dive into Mathematical Expressions
This article delves into the mathematical expression "9 less than six times a number," exploring its various interpretations, applications, and problem-solving techniques. We'll move beyond the simple equation and examine the broader concepts related to algebraic expressions, equation solving, and real-world applications. Understanding this seemingly simple phrase unlocks a world of mathematical possibilities.
Understanding the Core Expression
The phrase "9 less than six times a number" translates directly into an algebraic expression. Let's break it down step-by-step:
- A number: This is our unknown value, typically represented by a variable, often 'x'.
- Six times a number: This translates to 6 multiplied by x, written as 6x.
- 9 less than six times a number: This means we subtract 9 from 6x. Therefore, the complete algebraic expression is 6x - 9.
This expression forms the foundation for various mathematical problems and equations. The key is understanding the order of operations (PEMDAS/BODMAS) – multiplication before subtraction.
Constructing and Solving Equations
The expression 6x - 9 can be part of a larger equation. For example, we might encounter problems like:
- "9 less than six times a number is equal to 21." This translates to the equation: 6x - 9 = 21.
- "Find a number such that 9 less than six times the number is 0." This translates to: 6x - 9 = 0.
Solving these equations involves applying basic algebraic principles:
Solving 6x - 9 = 21:
- Add 9 to both sides: This isolates the term with 'x'. The equation becomes 6x = 30.
- Divide both sides by 6: This solves for 'x'. The solution is x = 5.
Solving 6x - 9 = 0:
- Add 9 to both sides: This gives 6x = 9.
- Divide both sides by 6: This yields x = 1.5 or x = 3/2.
These examples demonstrate how the initial expression forms the core of a solvable equation. The ability to translate word problems into algebraic expressions is crucial in mathematics.
Real-World Applications
The expression "9 less than six times a number" isn't just an abstract concept; it has practical applications in various real-world scenarios. Consider these examples:
Scenario 1: Calculating Profit
Imagine a business that sells a product for $6 each. Their fixed costs are $9. The profit (P) they make from selling 'x' number of products can be represented by the equation: P = 6x - 9.
If they sell 10 products (x=10), their profit would be 6(10) - 9 = $51. If they sell 5 products (x=5), their profit would be 6(5) - 9 = $21. This demonstrates how the expression helps calculate profit based on the number of units sold.
Scenario 2: Calculating Discounts
A store offers a discount of $9 on items that originally cost six times a certain base price ('x'). The final price (F) after the discount is: F = 6x - 9. If the base price is $2 (x=2), the final price would be 6(2) - 9 = $3.
Scenario 3: Geometry Problems
Consider a rectangle where the length is six times a certain measurement ('x') and the width is 9 units shorter than the length. The area (A) of the rectangle is given by: A = (6x)(6x - 9). This shows how the expression can be integrated into geometric calculations.
These scenarios illustrate the versatility of the expression and its applicability in diverse real-world problems.
Expanding the Concept: Variations and Extensions
We can build upon the core expression "6x - 9" to create more complex expressions and equations. Consider these variations:
-
Adding another variable: "9 less than six times a number, plus twice another number" would translate to 6x + 2y - 9. This introduces a new variable, 'y', and demonstrates the ability to incorporate multiple unknowns.
-
Introducing exponents: "9 less than six times the square of a number" would be 6x² - 9. This incorporates exponents, increasing the complexity of the expression and requiring more advanced algebraic techniques for solving equations involving it.
-
Inequalities: Instead of an equation, we could have an inequality like "9 less than six times a number is greater than 15," which translates to 6x - 9 > 15. Solving this requires different techniques, focusing on finding a range of values for 'x' that satisfy the inequality.
These variations highlight the adaptability of the basic expression and its potential to form the basis of more intricate mathematical problems.
Advanced Techniques and Concepts
Let's explore some advanced concepts related to the expression 6x - 9:
-
Graphing Linear Equations: The equation 6x - 9 = y represents a linear equation. Graphing this equation on a Cartesian plane helps visualize the relationship between 'x' and 'y', showing the slope and y-intercept. The slope of this line is 6, indicating that for every unit increase in x, y increases by 6. The y-intercept is -9, representing the point where the line intersects the y-axis.
-
Finding the Roots: Finding the roots (or zeros) of the equation 6x - 9 = 0 involves solving for the value of 'x' that makes the equation true (as shown earlier). The root represents the x-intercept of the linear equation's graph.
-
Systems of Equations: The expression could be incorporated into a system of equations involving multiple variables and equations. Solving such systems would require techniques like substitution or elimination to find the values of all unknowns.
Conclusion: Mastering Mathematical Expressions
The seemingly simple expression "9 less than six times a number" provides a gateway to understanding more complex algebraic concepts. By breaking down the phrase, translating it into an algebraic expression, constructing and solving equations, and exploring real-world applications, we gain a deeper appreciation for the power and versatility of mathematical language. This foundational understanding forms the basis for more advanced mathematical studies and problem-solving skills applicable in various fields. Remember that consistent practice and application are key to mastering these concepts. The ability to translate word problems into algebraic expressions, solve equations, and apply these skills to real-world situations is a vital asset in numerous academic and professional pursuits.
Latest Posts
Latest Posts
-
What Record Did The Nereus Break In May 2009
Jun 04, 2025
-
Which Transformations Can Be Used To Carry Abcd Onto Itself
Jun 04, 2025
-
Which Statement About Proportional Relationships Is False
Jun 04, 2025
-
Birds Of Many Species Ingest Foods Containing Carotenoids
Jun 04, 2025
-
Select All The Characteristics That Describe Bart Ks Instrumental Music
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about 9 Less Than Six Times A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.