9x + 8x - 12 + 7
Breaking News Today
Jun 01, 2025 · 5 min read
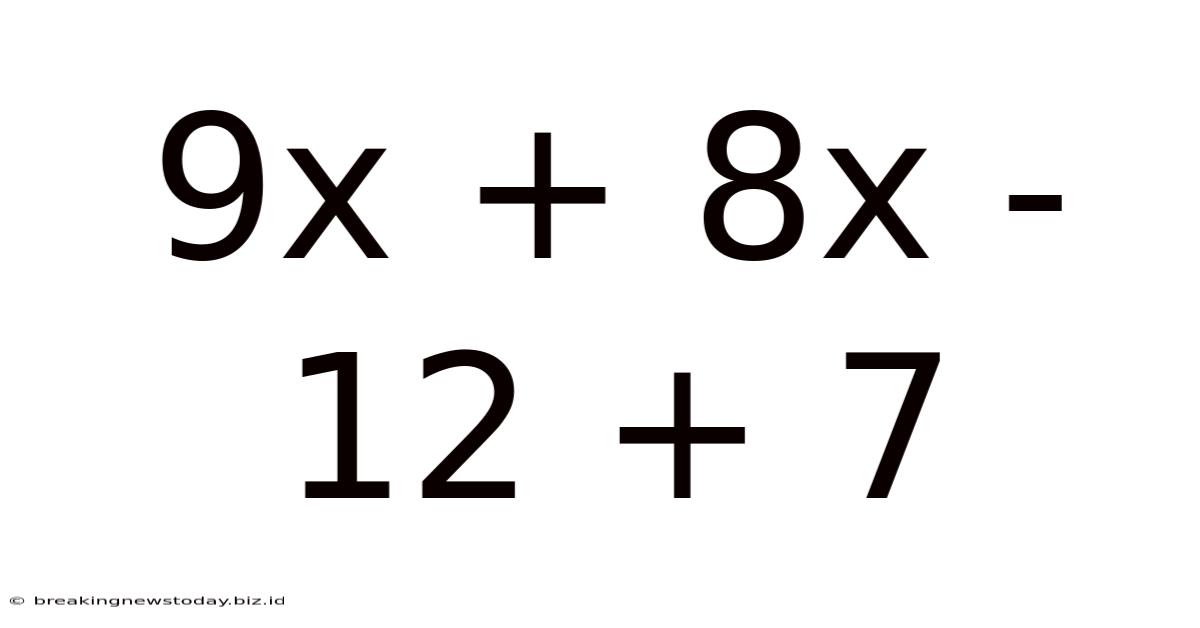
Table of Contents
Demystifying the Equation: 9x + 8x - 12 + 7
This article delves into the seemingly simple equation, 9x + 8x - 12 + 7, exploring its solution, underlying mathematical concepts, and its relevance in various applications. We'll break down the problem step-by-step, providing a clear understanding for beginners and reinforcing concepts for more experienced learners. We’ll also touch upon the broader context of algebraic equations and their significance in various fields.
Understanding the Components of the Equation
Before diving into the solution, let's understand the different parts of the equation:
-
Variables: The equation contains a variable, 'x'. A variable is a symbol (usually a letter) that represents an unknown quantity or value. The goal is often to solve for the value of this variable.
-
Coefficients: The numbers that precede the variables are called coefficients. In our equation, 9 and 8 are the coefficients of 'x'. They indicate how many times the variable is being added to itself.
-
Constants: The numbers without variables are constants. In this case, -12 and 7 are the constants. Constants represent fixed values that do not change.
-
Operators: The symbols (+ and -) are operators that indicate mathematical operations to be performed: addition and subtraction.
Solving the Equation: A Step-by-Step Approach
The solution to the equation involves simplifying it by combining like terms. Like terms are terms that contain the same variables raised to the same power. In this case, both 9x and 8x are like terms because they both contain the variable 'x' raised to the power of 1 (which is typically not explicitly written).
Step 1: Combine like terms (variables):
9x + 8x = 17x
Step 2: Combine like terms (constants):
-12 + 7 = -5
Step 3: Rewrite the simplified equation:
The simplified equation becomes: 17x - 5
This is the simplest form of the original equation. It's important to note that we haven't solved for 'x' yet; we've only simplified the expression. To solve for 'x', we would need a complete equation, such as:
17x - 5 = 0 or 17x - 5 = 20, etc.
In these cases, we would use algebraic manipulation techniques to isolate 'x' on one side of the equation. For example, to solve 17x - 5 = 0:
- Add 5 to both sides: 17x = 5
- Divide both sides by 17: x = 5/17
Similarly, for 17x - 5 = 20:
- Add 5 to both sides: 17x = 25
- Divide both sides by 17: x = 25/17
The Significance of Algebraic Equations
The equation 9x + 8x - 12 + 7, while seemingly basic, represents a fundamental concept in algebra. Algebraic equations are the backbone of many mathematical and scientific fields. Their applications are vast and include:
-
Physics: Describing motion, forces, and energy relationships. Many physical laws are expressed as equations.
-
Engineering: Designing structures, circuits, and systems. Equations are crucial for ensuring stability, efficiency, and safety.
-
Chemistry: Calculating reaction rates, concentrations, and equilibrium constants. Stoichiometry relies heavily on equations.
-
Economics: Modeling economic growth, supply and demand, and financial markets. Equations are used to predict trends and make decisions.
-
Computer Science: Developing algorithms and solving computational problems. Equations are at the heart of programming logic.
Expanding on the Concepts: Beyond Simple Equations
While our example focuses on a straightforward linear equation, the principles extend to more complex equations:
-
Quadratic Equations: These equations involve the variable raised to the power of 2 (e.g., ax² + bx + c = 0). Solving these requires different techniques, such as factoring, the quadratic formula, or completing the square.
-
Simultaneous Equations: These involve multiple equations with multiple variables. Solutions involve solving the equations together to find values that satisfy all equations. Methods like substitution and elimination are commonly used.
-
Exponential Equations: These involve variables as exponents (e.g., aˣ = b). Solving these often requires logarithms.
-
Logarithmic Equations: These involve logarithms of variables (e.g., logₐ(x) = b). Solving these often requires exponential functions.
-
Differential Equations: These involve equations with derivatives, describing rates of change. They are crucial in modeling dynamic systems. These often require specialized techniques to solve.
Practical Applications and Real-World Examples
Let's illustrate how equations similar to 9x + 8x - 12 + 7 might appear in real-world scenarios:
Scenario 1: Calculating total cost:
Imagine you're buying items. You buy 9 items costing x dollars each and 8 more items costing x dollars each. You also have a discount of $12 and pay a $7 shipping fee. The total cost can be represented as: 9x + 8x - 12 + 7. If each item (x) costs $5, the total cost would be: 17(5) - 5 = $80.
Scenario 2: Calculating profit:
Suppose a business makes a profit of 9x dollars from one product line and 8x dollars from another. They have expenses of $12 and additional income of $7 from other sources. The total profit can be represented by the same equation: 9x + 8x - 12 + 7.
Scenario 3: Solving for an unknown quantity:
Imagine you're working with a formula where a part of the formula simplifies to 17x - 5. If you know the value of the overall formula, you can then solve for x. This happens frequently in physics, engineering, and other quantitative fields.
Mastering Algebra: Resources and Further Learning
This article provides a foundational understanding of the equation 9x + 8x - 12 + 7 and its underlying principles. To further enhance your understanding of algebra and equation solving, consider exploring the following resources:
-
Khan Academy: This online platform offers comprehensive courses on algebra and related topics, with videos, practice exercises, and personalized feedback.
-
Textbook Resources: Many excellent algebra textbooks are available, offering detailed explanations and numerous practice problems.
-
Online Tutorials: Numerous online tutorials and videos can provide supplementary learning and visual aids for understanding complex concepts.
By practicing regularly and utilizing available resources, you can build a strong foundation in algebra and apply these principles to various real-world problems. Remember, mastering algebra is a journey; consistent effort and a curious mind are key to success. Start with the fundamentals, like our simple equation, and gradually progress towards more complex concepts. The skills you acquire will be invaluable across numerous disciplines.
Latest Posts
Latest Posts
-
Which Statement Best Describes How Igneous Rocks Are Formed
Jun 02, 2025
-
Match The Description Of The Murmur To The Valvular Lesion
Jun 02, 2025
-
87 5 Of What Number Is 49
Jun 02, 2025
-
Apples Mail And Microsofts Outlook Are Examples Of A
Jun 02, 2025
-
Which Documentation Practices Are Shown In The Following Workflow
Jun 02, 2025
Related Post
Thank you for visiting our website which covers about 9x + 8x - 12 + 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.