9x Y 45 Solve For Y
Breaking News Today
Jun 07, 2025 · 6 min read
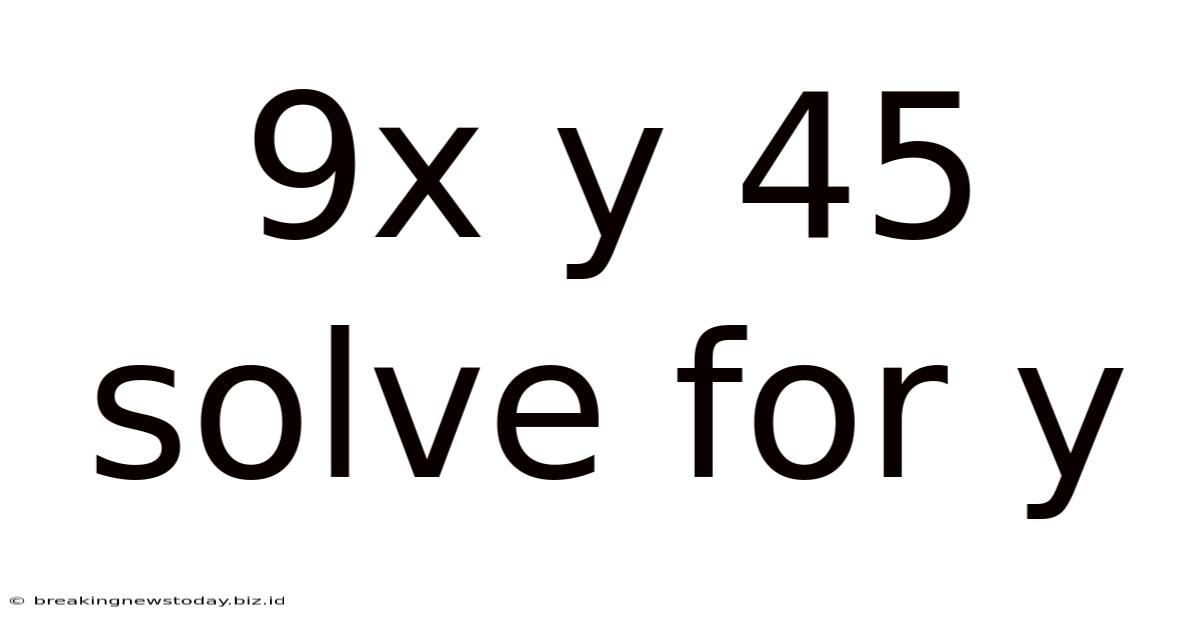
Table of Contents
Solving for y: A Comprehensive Guide to 9x + y = 45
This article provides a thorough explanation of how to solve the algebraic equation 9x + y = 45 for y. We'll explore various approaches, delve into the underlying concepts, and offer practical examples to solidify your understanding. Whether you're a student brushing up on your algebra skills or a curious learner, this guide will equip you with the knowledge to tackle similar equations with confidence.
Understanding the Equation: 9x + y = 45
The equation 9x + y = 45 is a linear equation in two variables, x and y. This means that when graphed, it represents a straight line. The goal is to isolate y, expressing it solely in terms of x. This process will reveal the relationship between x and y and allows us to find the value of y for any given value of x.
Key Concepts:
- Variables: 'x' and 'y' are variables representing unknown quantities.
- Constants: '9' and '45' are constants, representing fixed numerical values.
- Coefficients: '9' is the coefficient of x, indicating the multiplicative relationship between x and the term 9x.
- Solving for a Variable: The process of isolating a variable (in this case, y) to one side of the equation to express it in terms of other variables and constants.
Methods for Solving for y in 9x + y = 45
There are several ways to solve for y. Let's explore the most common methods:
Method 1: Subtraction Property of Equality
This method relies on the fundamental principle that subtracting the same value from both sides of an equation maintains the equality.
-
Identify the term with y: In the equation 9x + y = 45, the term with y is +y.
-
Isolate the y term: To isolate 'y', we need to eliminate the 9x term. We can do this by subtracting 9x from both sides of the equation:
9x + y - 9x = 45 - 9x
-
Simplify: This simplifies to:
y = 45 - 9x
Therefore, the solution for y is y = 45 - 9x. This equation tells us that for any given value of x, we can calculate the corresponding value of y.
Method 2: Transposition Method
The transposition method is a shortcut of the subtraction property of equality. It involves moving a term from one side of the equation to the other by changing its sign.
-
Identify the term with y: Again, the term with y is +y.
-
Transpose 9x: We move the 9x term to the right side of the equation, changing its sign from positive to negative:
y = 45 - 9x
This directly yields the solution: y = 45 - 9x.
Verifying the Solution
It's crucial to verify the solution to ensure accuracy. Let's test our solution with a few example values of x:
-
If x = 0: y = 45 - 9(0) = 45. Substituting x = 0 and y = 45 into the original equation: 9(0) + 45 = 45, which is true.
-
If x = 1: y = 45 - 9(1) = 36. Substituting x = 1 and y = 36 into the original equation: 9(1) + 36 = 45, which is true.
-
If x = 5: y = 45 - 9(5) = 0. Substituting x = 5 and y = 0 into the original equation: 9(5) + 0 = 45, which is true.
These examples confirm that our solution, y = 45 - 9x, is correct.
Applications and Extensions
The ability to solve for a variable in a linear equation has broad applications across various fields:
1. Linear Relationships in Real-World Problems
Many real-world scenarios can be modeled using linear equations. For example:
-
Cost Calculation: Imagine a scenario where the total cost (y) of producing x units of a product is given by the equation 9x + y = 45, where 9 represents the cost per unit and 45 represents fixed overhead costs. Solving for y allows you to determine the total cost for any number of units produced.
-
Profit Analysis: If 9x represents revenue and 45 represents total expenses, solving for y would reveal the profit for a given number of units sold (x).
-
Distance-Time Problems: Linear equations can model relationships between distance, speed, and time. If 9x represents distance covered at a certain speed and 45 represents total distance, y could represent the remaining distance to cover.
2. Graphing Linear Equations
The solution y = 45 - 9x allows us to easily graph the linear equation. We can select different values for x, calculate the corresponding y values using the equation, and plot these points on a coordinate plane. The resulting line will visually represent all the possible (x, y) pairs that satisfy the equation 9x + y = 45.
3. System of Equations
Solving for y in 9x + y = 45 becomes particularly useful when dealing with systems of equations. If you have another equation involving x and y, you can use substitution (replacing y with 45 - 9x) to solve for both x and y simultaneously.
4. Advanced Algebraic Concepts
The foundational skill of solving for a variable in a linear equation is crucial for understanding more advanced algebraic concepts like:
-
Linear Inequalities: The same principles apply when dealing with inequalities (e.g., 9x + y > 45).
-
Functions: The equation y = 45 - 9x can be expressed as a function: f(x) = 45 - 9x, demonstrating the concept of a dependent variable (y) depending on an independent variable (x).
-
Slope-Intercept Form: The equation y = 45 - 9x is already in slope-intercept form (y = mx + b), where -9 is the slope (m) and 45 is the y-intercept (b). This form makes it easy to identify key characteristics of the line.
Troubleshooting Common Mistakes
While solving for y in 9x + y = 45 is relatively straightforward, certain mistakes can occur:
-
Incorrect Sign Changes: Ensure you change the sign of the term when moving it to the other side of the equation. A common error is forgetting to change the sign from positive to negative (or vice versa).
-
Order of Operations: Remember to follow the order of operations (PEMDAS/BODMAS) when simplifying the equation, especially if it involves more complex expressions.
-
Algebraic Errors: Carefully check your calculations throughout the process to avoid simple arithmetic or algebraic mistakes.
Conclusion: Mastering the Fundamentals of Algebra
Solving for y in the equation 9x + y = 45 is a fundamental skill in algebra. By mastering this process, you build a solid foundation for tackling more complex algebraic problems and applying these concepts to real-world scenarios. Understanding the underlying principles, practicing different methods, and verifying your solutions will ensure your success in solving similar equations and progressing to more advanced mathematical concepts. Remember to practice regularly and seek clarification when needed – the path to mastering algebra is built on consistent effort and a deep understanding of the fundamentals.
Latest Posts
Latest Posts
-
Tim Is Confined To A Nursing Home
Jun 07, 2025
-
25 4x 15 3x 10 X
Jun 07, 2025
-
Which Sentence Is True About Abstaining From Sex
Jun 07, 2025
-
Which Statements Accurately Compare Beowulf And Grendel Select 2 Options
Jun 07, 2025
-
Which Statement Best Sums Up The Meaning Of Jesuss Words
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about 9x Y 45 Solve For Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.