A 9y 3yx Solve For Y
Breaking News Today
Jun 04, 2025 · 5 min read
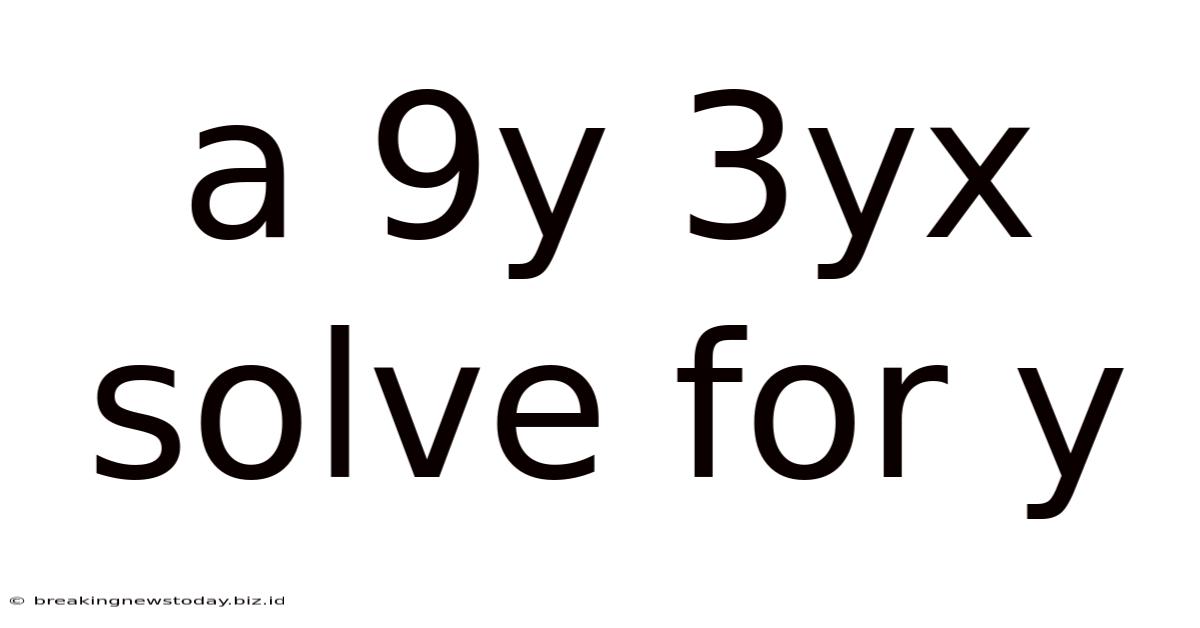
Table of Contents
Solving for 'y': A Comprehensive Guide to 9y + 3yx = ?
This article delves deep into the algebraic equation 9y + 3yx = ?, exploring various methods to solve for 'y' depending on the context and additional information provided. We'll cover scenarios where the equation is solvable and those where it's not, emphasizing the importance of understanding the underlying mathematical principles. We will also touch upon the broader implications of solving algebraic equations and their applications in various fields.
Understanding the Equation: 9y + 3yx
The equation 9y + 3yx = ? presents a classic algebraic challenge. The presence of 'y' in multiple terms signifies a need for careful manipulation to isolate 'y' and determine its value. However, the equation itself isn't fully defined; it's an incomplete equation. We need an additional piece of information—a value for the expression or another equation—to find a numerical solution for 'y'.
The Role of 'x'
The variable 'x' plays a crucial role. Its presence makes the equation more complex. Without knowing the value of 'x', we cannot find a single numerical solution for 'y'. The solution for 'y' will be expressed in terms of x. This means our final answer will be an algebraic expression containing 'x'.
Methods for Solving (with assumptions)
To proceed, we'll consider different scenarios by making assumptions about the missing information.
Scenario 1: Solving for 'y' when the equation equals a number
Let's assume the equation equals a constant, say 'k'. Our equation becomes:
9y + 3yx = k
Now, we can solve for 'y' using algebraic manipulation. The key is to factor out 'y' from both terms:
y(9 + 3x) = k
Now, to isolate 'y', we divide both sides by (9 + 3x):
y = k / (9 + 3x)
This is the solution for 'y' in terms of 'x' and 'k'. Note: This solution is only valid if (9 + 3x) is not equal to zero. If 9 + 3x = 0, then x = -3, and the equation becomes undefined (division by zero is undefined). This illustrates an important concept in algebra: the existence of solutions depends on the values of the variables.
Scenario 2: Solving for 'y' when another equation is given
Let's suppose we have a second equation involving 'x' and 'y'. For instance:
x = 2y - 5
Now we have a system of two equations:
- 9y + 3yx = k
- x = 2y - 5
We can solve this system using substitution or elimination. Let's use substitution. We substitute the expression for 'x' from equation (2) into equation (1):
9y + 3y(2y - 5) = k
Expanding and simplifying:
9y + 6y² - 15y = k
Rearranging into a quadratic equation:
6y² - 6y - k = 0
This quadratic equation can be solved using the quadratic formula:
y = [-b ± √(b² - 4ac)] / 2a
where a = 6, b = -6, and c = -k.
This provides two possible solutions for 'y', depending on the value of 'k' and the discriminant (b² - 4ac). The nature of the solutions (real, imaginary, or repeated) depends on the value of the discriminant. If the discriminant is negative, the solutions will be imaginary. If it is zero, there will be one repeated real solution, and if positive, there will be two distinct real solutions.
Scenario 3: Solving for 'y' when k=0
Let's set k=0 in our original equation:
9y + 3yx = 0
Factoring out y:
y(9 + 3x) = 0
This equation has two solutions:
- y = 0 (one solution)
- 9 + 3x = 0 => x = -3 (this gives us the value of x that results in y being able to take on any value. Any value of y will satisfy the equation when x=-3)
This demonstrates that sometimes, even without a specific value assigned to the expression, we can still find solutions for 'y' depending on the values of other variables.
Expanding the Scope: Applications and Implications
The techniques demonstrated above are fundamental to solving various algebraic problems in diverse fields. Here are some examples:
-
Physics: Solving for unknowns in kinematic equations. For instance, finding final velocity (y) given initial velocity, acceleration (x), and time.
-
Engineering: Analyzing circuits, determining stress and strain in materials, and solving for variables in structural design.
-
Economics: Modelling economic growth, analyzing market equilibrium, and predicting consumer behavior.
-
Computer Science: Developing algorithms, working with data structures, and building simulations.
Importance of Understanding the Limitations
It's crucial to acknowledge the limitations in solving algebraic equations. Without sufficient information, a single, unique solution might not exist. Understanding these limitations prevents errors and helps you interpret the results accurately.
Practical Tips for Solving Algebraic Equations
- Identify the unknowns: Clearly define the variables and what you need to solve for.
- Simplify the equation: Combine like terms and rearrange the equation to isolate the variable of interest.
- Check your solution: Substitute the solution back into the original equation to verify its accuracy.
- Use multiple methods: If one method fails, try another. Substitution, elimination, and factoring are common techniques.
- Graphing: Use graphing tools to visualize the equations and find approximate solutions.
Conclusion
Solving for 'y' in the equation 9y + 3yx = ? requires contextual information. We explored different scenarios showing how additional data or assumptions lead to different solutions. The methods employed—factoring, substitution, and solving quadratic equations—illustrate fundamental algebraic principles applicable to a wide range of problems across various disciplines. Understanding the limitations and applying sound problem-solving techniques is crucial for accurate and meaningful results. Mastering these skills is essential for success in mathematics and its related fields. Remember to always check your work and consider the potential limitations of your solutions.
Latest Posts
Latest Posts
-
Which Of The Following Can Provoke A Rejection Syndrome
Jun 06, 2025
-
Which Statement Is Not True About Endurance Training
Jun 06, 2025
-
Which Of The Following Best Describes Deflation
Jun 06, 2025
-
Security Personnel Whose Post Is Located Outside The Entrance
Jun 06, 2025
-
Day By Day The Work Assumed Greater Precision
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about A 9y 3yx Solve For Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.