A Line Is An Undefined Term Because It
Breaking News Today
Mar 28, 2025 · 5 min read
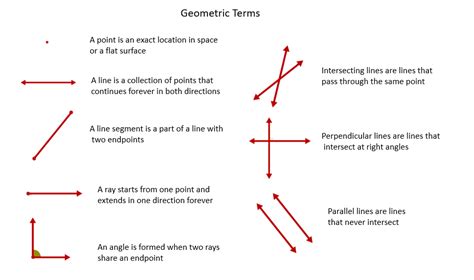
Table of Contents
- A Line Is An Undefined Term Because It
- Table of Contents
- A Line is an Undefined Term Because It… Needs No Definition! Understanding Axiomatic Systems in Geometry
- The Necessity of Undefined Terms: The Foundation of Geometric Logic
- Why "Line" Remains Undefined
- Building Upon Undefined Terms: Defining Other Geometric Concepts
- The Role of Axioms and Postulates: Rules of the Geometric Game
- Exploring Different Geometric Systems: Euclidean vs. Non-Euclidean
- Beyond the Basics: Advanced Concepts and Applications
- Conclusion: The Power of Undefined Terms
- Latest Posts
- Latest Posts
- Related Post
A Line is an Undefined Term Because It… Needs No Definition! Understanding Axiomatic Systems in Geometry
Geometry, at its core, is the study of shapes, sizes, relative positions of figures, and the properties of space. To build a robust and consistent system of geometric knowledge, mathematicians rely on a foundational structure: axiomatic systems. These systems begin with undefined terms, statements that are accepted without formal definition, acting as the building blocks for all subsequent definitions and theorems. A line is a prime example of an undefined term, and understanding why it's undefined is key to grasping the power and elegance of geometry.
The Necessity of Undefined Terms: The Foundation of Geometric Logic
Why can't we just define everything? The problem lies in circular definitions. If we attempt to define every term, we inevitably run into a loop where the definition of one term relies on another, which relies on a third, and so on, leading to an infinite regress. To avoid this logical trap, mathematicians wisely choose a select few terms to remain undefined. These foundational concepts, including the line, are the bedrock upon which the entire edifice of geometric knowledge is constructed.
Why "Line" Remains Undefined
The concept of a "line" is so fundamental that attempting to define it invariably involves terms that themselves need definition, creating the aforementioned circularity. For example, consider these attempted definitions:
- A line is a straight path of infinite length. This definition relies on the undefined terms "straight" and "infinite." What exactly is straight? How do we define "infinite" in a way that is not inherently geometric?
- A line is a set of points that extend infinitely in opposite directions. This definition relies on the undefined terms "point" and "extend." While we have an intuitive understanding of these terms, formally defining them leads to circular definitions or requires even more fundamental, undefined concepts.
- A line is the shortest distance between two points. This definition hinges on the already undefined concepts of "distance" and "shortest."
Each attempt to define "line" introduces other terms that demand their own definitions, pushing the process indefinitely. The elegant solution? We simply accept "line" as an undefined term, a basic concept that we understand intuitively and use as a starting point for building our geometric framework.
Building Upon Undefined Terms: Defining Other Geometric Concepts
Once we accept "line" as undefined, we can use it to define other geometric terms. For instance:
- Point: We can describe a point as a location in space that has no size or dimension, but a point lies on a line, demonstrating the line's more fundamental nature.
- Plane: A plane is a flat surface that extends infinitely in all directions. We can define a plane as a set of points, and often illustrate its relationship to lines by stating that it contains at least three non-collinear points (points not lying on the same line).
- Segment: A line segment is a part of a line bounded by two points, known as its endpoints.
- Ray: A ray is a part of a line that starts at a point and extends infinitely in one direction.
These definitions rely on the undefined term "line" and the intuitive understanding of "point" as something that can exist on a line or in a plane.
The Role of Axioms and Postulates: Rules of the Geometric Game
Beyond undefined terms, axiomatic systems also include axioms or postulates. These are statements that are accepted as true without proof. They provide the rules of the game, governing how we manipulate and reason about the undefined terms and their defined counterparts. Examples of axioms related to lines include:
- Two points determine a line: Given any two distinct points, there exists exactly one line that passes through both points.
- A line contains infinitely many points: This axiom emphasizes the boundless nature of a line.
- Two distinct lines intersect at most at one point. This axiom establishes the relationships between two separate lines. It lays groundwork for further understanding of parallel and intersecting lines.
These axioms, in conjunction with the undefined terms, form the foundation for deriving theorems and proving geometric properties. Theorems are statements that can be logically proven using previously established axioms, definitions, and other theorems.
Exploring Different Geometric Systems: Euclidean vs. Non-Euclidean
The Euclidean geometry we commonly learn in school is based on a specific set of axioms, including those related to lines. However, different axiomatic systems exist, leading to different types of geometries. Non-Euclidean geometries, for example, modify or replace Euclid's parallel postulate (which deals with parallel lines) leading to fundamentally different geometric properties and spatial interpretations. The understanding of "line" as an undefined term allows for this flexibility. The underlying concept of a line can remain intuitively similar, but its properties and relationships within the geometric system are dictated by the specific axioms adopted.
Beyond the Basics: Advanced Concepts and Applications
The seemingly simple concept of a line underpins incredibly complex and useful mathematical concepts. The idea of a line extends far beyond basic geometry:
- Linear Algebra: Lines are fundamental objects in linear algebra, forming the basis for vector spaces and linear transformations. They're represented by equations and manipulated using matrix operations.
- Calculus: Lines form the foundation for the concepts of tangents and derivatives, enabling us to study the rates of change and behavior of functions.
- Computer Graphics: Lines are the building blocks of computer-generated images. Algorithms for rendering images often involve manipulating and calculating properties of lines and their intersections.
- Physics and Engineering: Lines are frequently used to model trajectories, forces, and other physical phenomena.
Conclusion: The Power of Undefined Terms
The decision to leave "line" undefined is not an oversight but a deliberate choice reflecting the fundamental nature of geometric reasoning. By accepting certain terms as undefined, we avoid circular definitions and create a robust and flexible system for studying space and shapes. Understanding the role of undefined terms, axioms, and theorems allows for a deeper appreciation of the power and elegance of geometric systems, underpinning the development of sophisticated mathematical concepts and real-world applications. The seemingly simple "line," as an undefined term, is a testament to the elegance of mathematical foundations. It's a building block of knowledge, accepted as a given, which allows for the construction of complex geometrical truths. This acceptance of an undefined term is critical to unlocking a vast and intriguing universe of mathematical possibilities.
Latest Posts
Latest Posts
-
Anatomy And Physiology Lab Practical 1 Quizlet
Mar 31, 2025
-
The Consideration Clause Of An Insurance Contract Includes
Mar 31, 2025
-
A Warning Sign Or Symptom Of Alcohol Poisoning Is Quizlet
Mar 31, 2025
-
Gonorrhea And Chlamydial Infection Are Associated With Quizlet
Mar 31, 2025
-
An Example Of Unfair Discrimination Would Be Quizlet
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about A Line Is An Undefined Term Because It . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
