A Number B Divided By Thirty-six
Breaking News Today
Jun 03, 2025 · 6 min read
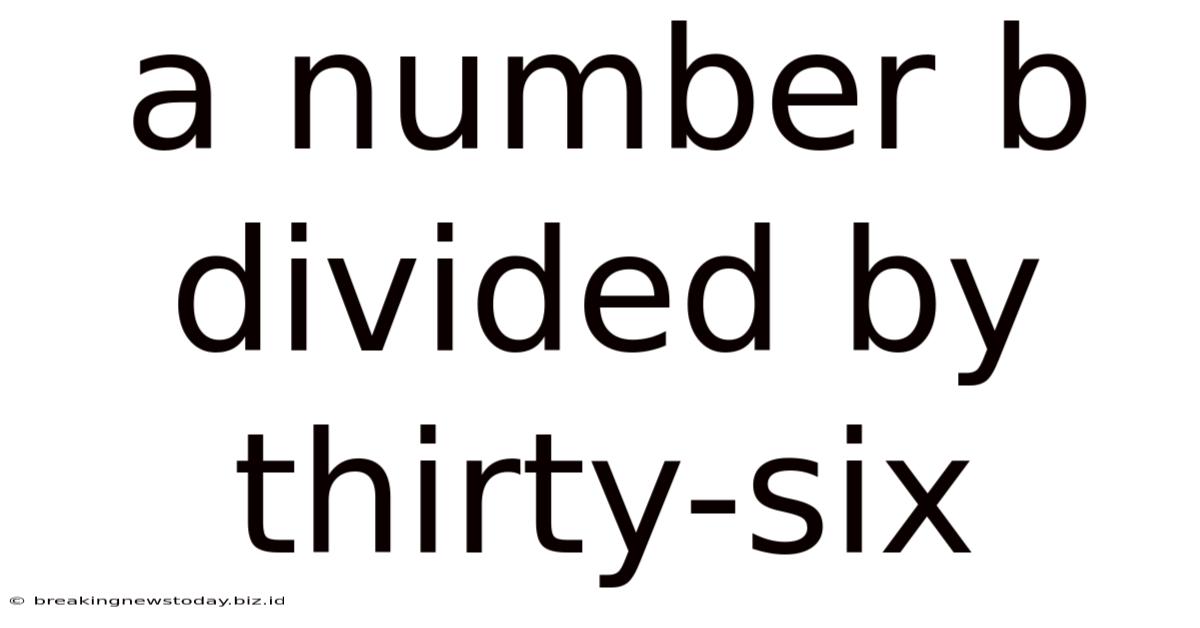
Table of Contents
A Number B Divided by Thirty-Six: Exploring the Mathematical Landscape
The seemingly simple operation of dividing a number 'b' by thirty-six opens a vast landscape of mathematical exploration. This seemingly straightforward calculation touches upon fundamental arithmetic principles, delves into the intricacies of divisibility rules, and even extends into more advanced concepts like modular arithmetic and abstract algebra. This article will delve deep into the multifaceted aspects of this division, exploring its practical applications, theoretical underpinnings, and the diverse ways it manifests in various mathematical contexts.
Understanding the Basics: Division and its Properties
At its core, dividing a number 'b' by thirty-six (represented as b/36 or b ÷ 36) means determining how many times thirty-six fits into 'b' completely. The result of this division can take several forms:
- Whole Number: If 'b' is a multiple of 36, the result will be a whole number (an integer). For example, 72/36 = 2.
- Fraction or Decimal: If 'b' is not a multiple of 36, the result will be a fraction or a decimal number. For example, 75/36 = 2.08333... or 25/12.
- Undefined: If 'b' is zero, the result is undefined as division by zero is an indeterminate form in mathematics.
The outcome of b/36 significantly depends on the value of 'b'. Understanding the properties of 'b' – whether it’s positive, negative, odd, even, prime, composite, etc. – influences the nature of the resultant quotient.
Divisibility Rules and Their Relevance
Before diving into the division itself, checking for divisibility by 36 can simplify the calculation. A number is divisible by 36 if it's divisible by both 4 and 9. This stems from the prime factorization of 36 (2² x 3²). Therefore, to check divisibility by 36:
- Divisibility by 4: The last two digits of the number must be divisible by 4.
- Divisibility by 9: The sum of the digits of the number must be divisible by 9.
If both conditions are met, the number is divisible by 36. This pre-division check drastically speeds up the process, especially when dealing with large numbers.
Exploring Different Scenarios: Types of Numbers 'b'
Let's examine how the division behaves with different kinds of numbers for 'b':
1. When 'b' is a Multiple of 36
If 'b' is a multiple of 36 (e.g., 72, 108, 144, ...), the division results in a whole number. This signifies that 36 divides 'b' evenly, leaving no remainder. The quotient represents the number of times 36 is contained within 'b'. This scenario is straightforward and fundamental to understanding the concept of divisibility.
2. When 'b' is not a Multiple of 36
This is where the division becomes more interesting. The result will be either a fraction or a decimal number. This fractional or decimal part represents the remainder after dividing 'b' by 36. This remainder is crucial in many applications, such as finding the remainder in modular arithmetic or determining the cyclical patterns in repeating decimals.
3. When 'b' is a Prime Number
Prime numbers are only divisible by 1 and themselves. Therefore, if 'b' is a prime number, the result of b/36 will always be a fraction or a decimal number, less than 1 unless b is greater than 36. The quotient will represent a fraction that has 36 as the denominator and the prime number as the numerator.
4. When 'b' is a Negative Number
If 'b' is a negative number, the result of b/36 will also be a negative number. The absolute value of the result remains the same, only the sign changes. This follows the standard rules of division with negative numbers.
5. When 'b' is Zero
As mentioned before, division by zero is undefined. This is a fundamental rule in mathematics. Trying to divide zero by 36 will lead to an error. Attempting to perform the operation in any programming language or calculator would generate an error message.
Applications of b/36: Real-World Examples
The division of a number 'b' by 36 appears in numerous contexts:
- Measurement Conversions: Converting measurements from one unit to another often involves division. For instance, converting inches to yards involves dividing by 36 (since there are 36 inches in a yard).
- Time Calculations: Calculating the number of hours from a given number of seconds involves dividing by 3600 (60 seconds/minute * 60 minutes/hour). Similarly, converting seconds to minutes will require division by 60.
- Inventory Management: Dividing the total number of items in a warehouse by 36 might be used to determine the number of shelves needed if each shelf can hold 36 items.
- Resource Allocation: If you have 'b' resources to distribute evenly among 36 groups, dividing 'b' by 36 provides the amount each group receives.
- Modular Arithmetic: The remainder when 'b' is divided by 36 is crucial in modular arithmetic (clock arithmetic), where we are only concerned with the remainder after division.
Beyond the Basics: Advanced Concepts
The seemingly simple operation of b/36 touches upon several advanced mathematical concepts:
1. Modular Arithmetic (Modulo 36)
The remainder when 'b' is divided by 36 is denoted as b mod 36. This operation is fundamental in cryptography, computer science, and number theory. For instance, in a 36-hour clock system (a hypothetical system), the time after 40 hours would be 4 hours (40 mod 36 = 4).
2. Continued Fractions
If b/36 results in a non-terminating decimal, it can be expressed as a continued fraction – an expression of the form a₀ + 1/(a₁ + 1/(a₂ + ...)). Continued fractions offer a unique way to represent rational and irrational numbers.
3. Abstract Algebra
The concept of division extends into abstract algebra, where we explore mathematical structures like groups, rings, and fields. In these structures, division might not always be defined for all elements, and the properties of division can be significantly different from what we see in basic arithmetic.
Conclusion: The Richness of a Simple Division
The act of dividing a number 'b' by 36, while seemingly basic, reveals a rich tapestry of mathematical connections and practical applications. From fundamental divisibility rules to advanced concepts like modular arithmetic and continued fractions, this operation provides a gateway to explore the beauty and complexity of mathematics. Its diverse applications span various fields, highlighting its importance in both theoretical and practical settings. This exploration reveals the interconnectedness of mathematical ideas and the depth that can be found even in the simplest of operations. The seemingly simple process of dividing by 36 unveils layers of complexity that extend far beyond basic arithmetic, connecting to higher-level concepts and real-world applications, making it a fascinating area of mathematical study.
Latest Posts
Latest Posts
-
Which Irony Is Most Strongly Represented In The Story
Jun 05, 2025
-
A Technician Is Installing A New High End Video Adapter
Jun 05, 2025
-
What Happened When The Tree Saw A Ghost
Jun 05, 2025
-
Find The Difference Between 303 And 184
Jun 05, 2025
-
The Sixteenth Century Saw A Blossoming Of Instrumental Dance Music
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about A Number B Divided By Thirty-six . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.