A Number Is More Than 12 Units From 0
Breaking News Today
Jun 03, 2025 · 5 min read
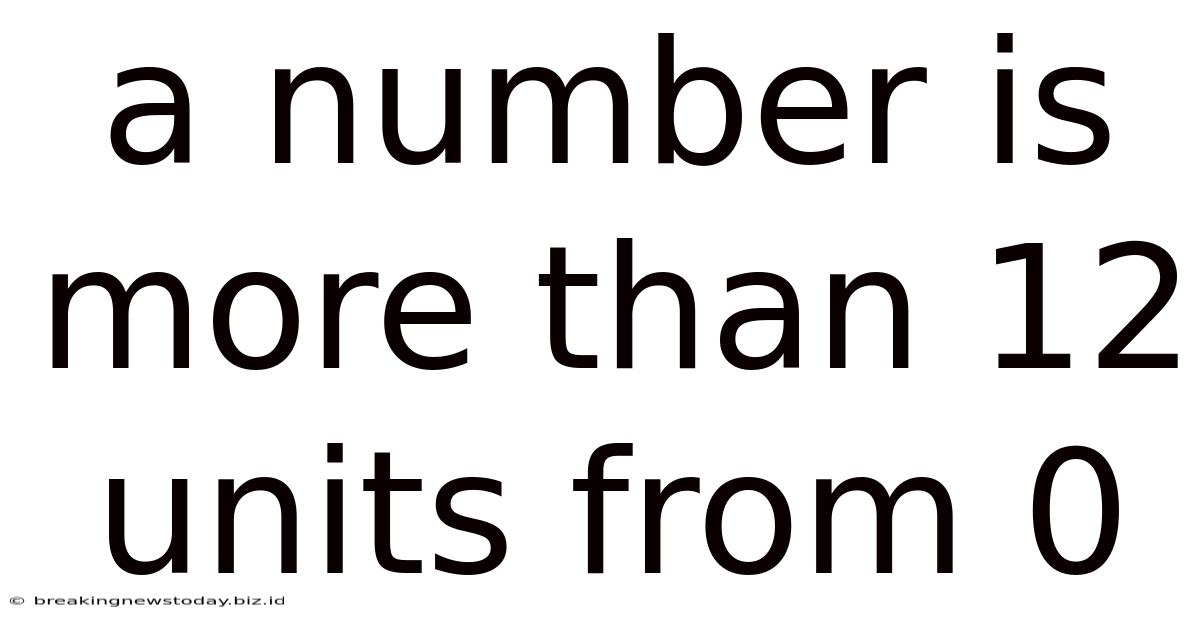
Table of Contents
A Number is More Than 12 Units from 0: Exploring Distance and Inequalities
This article delves into the mathematical concept of a number being more than 12 units away from zero, exploring its implications across various mathematical contexts, including number lines, inequalities, and absolute values. We'll examine how this concept is represented, solved, and applied in different scenarios. Understanding this concept is fundamental to grasping more complex mathematical ideas and solving real-world problems.
Understanding Distance on the Number Line
The core idea revolves around distance on a number line. Zero (0) serves as the origin or reference point. When we say a number is "more than 12 units from 0," we mean that the number's distance from zero is greater than 12. This distance is irrespective of whether the number is positive or negative. For instance, both -15 and 15 are more than 12 units away from 0 because their absolute distances from 0 are 15 units, which exceeds 12.
Visualizing on the Number Line
Imagine a number line stretching infinitely in both positive and negative directions. Zero is located at the center. Numbers greater than 0 are positioned to the right, and numbers less than 0 are to the left. A number is 12 units away from 0 if it's located at either +12 or -12. Any number beyond these points, either to the left of -12 or to the right of +12, is more than 12 units from 0.
Representing the Concept Mathematically
This concept can be expressed using inequalities and absolute values:
-
Inequalities: The condition "a number is more than 12 units from 0" can be represented by two separate inequalities:
x > 12orx < -12. This means the number x is either greater than 12 or less than -12. -
Absolute Value: A more concise way to represent this is using absolute value. The absolute value of a number, denoted as |x|, represents its distance from zero. Therefore, the condition "a number is more than 12 units from 0" can be written as:
|x| > 12. This single inequality encompasses both possibilities: numbers greater than 12 and numbers less than -12.
Solving Inequalities Involving Distance from Zero
Let's explore how to solve inequalities involving this concept.
Example 1: Solving |x| > 12
To solve |x| > 12, we need to consider two separate cases:
-
Case 1: x > 0: If x is positive, then |x| = x. The inequality becomes
x > 12. This means all numbers greater than 12 satisfy the condition. -
Case 2: x < 0: If x is negative, then |x| = -x. The inequality becomes
-x > 12. Multiplying both sides by -1 and flipping the inequality sign givesx < -12. This means all numbers less than -12 satisfy the condition.
Therefore, the solution to |x| > 12 is x > 12 or x < -12.
Example 2: Solving |x - 5| > 12
This example introduces a slight variation. Instead of the distance of x from 0, we're considering the distance of x - 5 from 0. We follow a similar approach:
-
Case 1: x - 5 > 0: This simplifies to
x - 5 > 12, which solves tox > 17. -
Case 2: x - 5 < 0: This simplifies to
-(x - 5) > 12, which becomes-x + 5 > 12. Solving this gives-x > 7, orx < -7.
Thus, the solution to |x - 5| > 12 is x > 17 or x < -7. This means any number greater than 17 or less than -7 is more than 12 units away from 5 on the number line.
Example 3: Real-World Application – Temperature Fluctuations
Imagine a scenario where the ideal temperature for a delicate experiment is 25°C. The experiment can only tolerate temperature fluctuations of more than 12°C from this ideal. We can model this using the inequality |T - 25| > 12, where T represents the temperature. Solving this, we find that the experiment will fail if the temperature is greater than 37°C or less than 13°C.
Connecting to Other Mathematical Concepts
The concept of a number being more than 12 units from 0 is deeply intertwined with other essential mathematical ideas:
Intervals and Set Notation
The solution sets to inequalities like |x| > 12 can be represented using interval notation and set notation. For |x| > 12, the solution set in interval notation is (-∞, -12) ∪ (12, ∞). This represents the union of two open intervals. In set notation, it might be written as {x ∈ ℝ | x < -12 or x > 12}.
Compound Inequalities
The two separate inequalities resulting from solving absolute value inequalities (e.g., x > 12 or x < -12) represent a compound inequality. These inequalities are often solved individually and then combined to provide the complete solution.
Graphing Inequalities
Inequalities involving distance from zero can be easily graphed on a number line. For |x| > 12, we would shade the regions to the left of -12 and to the right of 12. Open circles would be used at -12 and 12 to indicate that these values are not included in the solution.
Advanced Applications and Extensions
The fundamental concept of distance from zero extends beyond simple linear inequalities. It finds application in:
-
Calculus: Analyzing limits and continuity often involves considering the distance of a function's value from a particular point.
-
Statistics: The concept of standard deviation involves measuring the dispersion of data points from the mean, which is analogous to the distance from zero.
-
Linear Algebra: The concept of norm (a generalization of absolute value) in vector spaces measures the distance of a vector from the origin (the zero vector).
-
Complex Numbers: The modulus of a complex number represents its distance from the origin in the complex plane. Inequalities involving the modulus are used extensively in complex analysis.
Conclusion: The Significance of Distance from Zero
Understanding the concept of a number being more than 12 units from 0, or more generally, a distance from any reference point, is a cornerstone of various mathematical disciplines. Its representation using inequalities and absolute values, its graphical interpretation, and its applications in diverse fields highlight its importance. Mastering this concept lays a solid foundation for tackling more complex mathematical problems and appreciating the interconnectedness of seemingly disparate mathematical ideas. This fundamental concept bridges the gap between abstract mathematical theory and its tangible applications in the real world. By practicing solving these types of inequalities and visualizing them on the number line, you'll significantly enhance your mathematical skills and problem-solving abilities.
Latest Posts
Latest Posts
-
What Must Students Use When Summarizing An Informational Text
Jun 05, 2025
-
Which Of The Following Bands Was Integrated
Jun 05, 2025
-
A Charge Nurse Is Teaching Adult Cardiopulmonary Resuscitation
Jun 05, 2025
-
The Are Nomadic Hunter Gatherers Who Inhabit The Kalahari Desert
Jun 05, 2025
-
Match Each Example With The Subsystem It Belongs To
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about A Number Is More Than 12 Units From 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.