A Number N Plus 8 Is Greater Than 11
Breaking News Today
Jun 04, 2025 · 5 min read
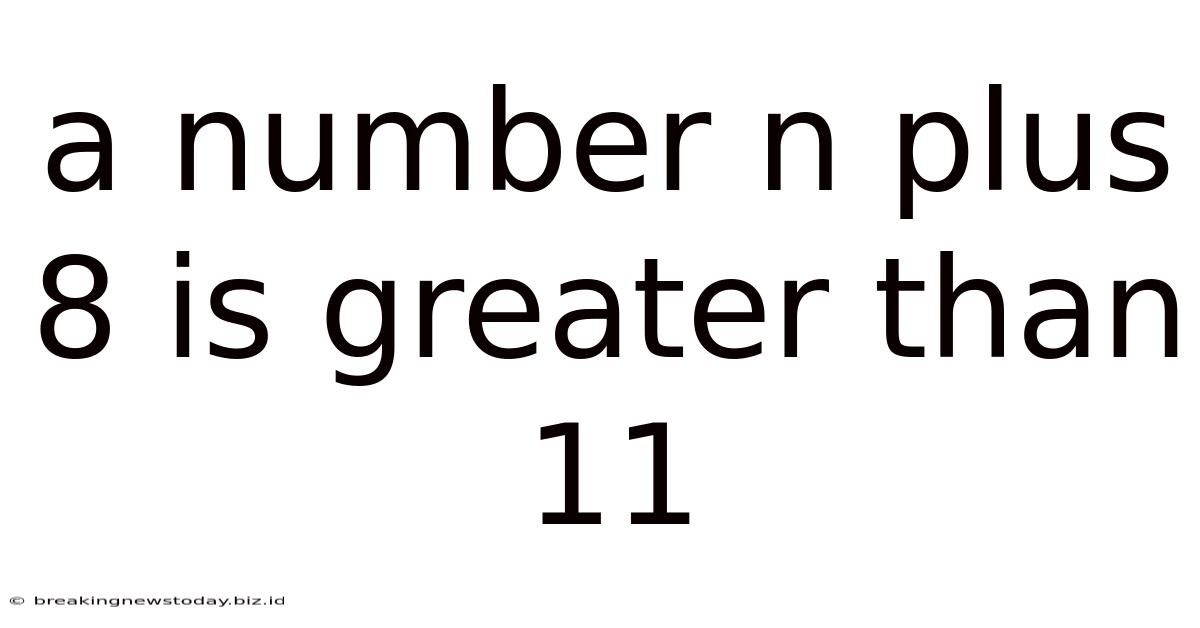
Table of Contents
A Number n Plus 8 is Greater Than 11: A Deep Dive into Inequalities
This seemingly simple statement, "a number n plus 8 is greater than 11," opens the door to a fascinating exploration of inequalities, their applications, and their broader significance in mathematics and beyond. This article will delve into this inequality, examining its solution, exploring its graphical representation, and extending the concept to more complex scenarios. We'll also touch upon the real-world applications of such mathematical concepts.
Understanding the Inequality: n + 8 > 11
The core of the problem lies in the inequality: n + 8 > 11. This statement asserts that the sum of an unknown number (n) and 8 is greater than 11. Our goal is to find the range of values for n that satisfy this condition.
Solving the Inequality
To solve this inequality, we employ the same principles used in solving equations, with one crucial difference: when multiplying or dividing by a negative number, the inequality sign flips. In this case, we need to isolate n.
- Subtract 8 from both sides: This step maintains the inequality's balance. Subtracting 8 from both sides gives us:
n + 8 - 8 > 11 - 8 n > 3
This solution tells us that n must be greater than 3. This means any number larger than 3 will satisfy the original inequality. For example, 4, 10, 100, and even 3.0001 are all valid solutions. However, 3 itself is not a solution because 3 + 8 = 11, and 11 is not greater than 11.
Graphical Representation
Visualizing the solution can provide a deeper understanding. We can represent the solution set on a number line.
The Number Line Representation
Draw a number line with 0 in the center and extend it in both positive and negative directions. Locate the number 3 on the line. Since n is greater than 3, we draw an open circle at 3 (to indicate that 3 is not included in the solution set) and shade the region to the right of 3, extending infinitely. This shaded region represents all possible values of n that satisfy the inequality.
[Insert image here: A number line with an open circle at 3 and the region to the right shaded. Label the shaded region "n > 3"]
This graphical representation provides a clear and concise visualization of the solution set, making it readily understandable.
Extending the Concept: More Complex Inequalities
The basic principle of solving inequalities can be extended to more complex scenarios involving multiple operations and variables.
Inequalities with Multiple Operations
Consider an inequality like: 2n + 5 < 17. To solve this, we follow a similar step-by-step approach:
- Subtract 5 from both sides: 2n < 12
- Divide both sides by 2: n < 6
The solution is n < 6. This means any number less than 6 satisfies the inequality. The graphical representation would be an open circle at 6 and the region to the left shaded.
Compound Inequalities
Compound inequalities involve two or more inequalities combined using "and" or "or". For example:
3n - 2 > 7 and n + 4 < 10
We solve each inequality separately:
- 3n - 2 > 7: This simplifies to n > 3
- n + 4 < 10: This simplifies to n < 6
Since it's an "and" condition, the solution is the intersection of both solution sets – the values of n that are both greater than 3 and less than 6. This can be written as 3 < n < 6.
The graphical representation would show the shaded region between 3 and 6 (excluding 3 and 6).
[Insert image here: A number line with the region between 3 and 6 shaded, with open circles at 3 and 6.]
Absolute Value Inequalities
Absolute value inequalities introduce another layer of complexity. For example:
|n - 2| > 5
This inequality means that the distance between n and 2 is greater than 5. To solve this, we consider two separate cases:
- n - 2 > 5: This simplifies to n > 7
- n - 2 < -5: This simplifies to n < -3
The solution is n > 7 or n < -3. The graphical representation would show two shaded regions: one to the right of 7 and one to the left of -3.
[Insert image here: A number line with the regions to the left of -3 and to the right of 7 shaded, with open circles at -3 and 7.]
Real-World Applications
Inequalities are not just abstract mathematical concepts; they have numerous practical applications in various fields.
Everyday Life Applications
- Budgeting: Determining if you have enough money to buy something involves comparing your available funds (a number) to the item's cost (another number). If your funds are greater than the cost, you can afford it.
- Time Management: Planning your day and ensuring you have enough time to complete all tasks requires comparing time available to the time required for each task.
- Recipes: Adjusting recipes to feed more or fewer people necessitates scaling the ingredients proportionally.
Scientific and Engineering Applications
- Physics: Many physical laws are expressed as inequalities, such as the relationship between speed, distance, and time.
- Engineering: Designing structures and systems requires ensuring certain parameters fall within acceptable ranges, expressed as inequalities.
- Computer Science: Inequalities are fundamental in algorithm design and optimization.
Economics and Finance
- Profitability Analysis: Determining the break-even point or profit margin requires solving inequalities to find the range of values that result in profit.
- Investment Strategies: Evaluating the risk and return of different investment options involves comparing potential gains and losses, expressed through inequalities.
Conclusion
The seemingly simple inequality, "n + 8 > 11," serves as a gateway to a vast and powerful field of mathematics. Understanding inequalities, their solutions, and their graphical representations is essential for solving various real-world problems across numerous disciplines. By mastering these fundamental concepts, we equip ourselves with valuable tools for tackling complex scenarios and making informed decisions in diverse contexts. The ability to analyze and interpret inequalities empowers us to model, understand, and solve a wide array of challenges, from simple everyday tasks to sophisticated scientific and engineering applications. Therefore, a thorough grasp of this seemingly basic concept has far-reaching implications and practical benefits across various walks of life.
Latest Posts
Latest Posts
-
Which Sentence Describes An Object That Has Kinetic Energy
Jun 06, 2025
-
What Can We Use The Decision Making Matrix For Cpi
Jun 06, 2025
-
Business Owners Copyright Holders And Network Administrators Publish
Jun 06, 2025
-
Besides Other Cars With What Or With Whom
Jun 06, 2025
-
Find The Sum Of 914 And 878
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about A Number N Plus 8 Is Greater Than 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.