Bh Hr 25 Solve For H
Breaking News Today
Jun 04, 2025 · 5 min read
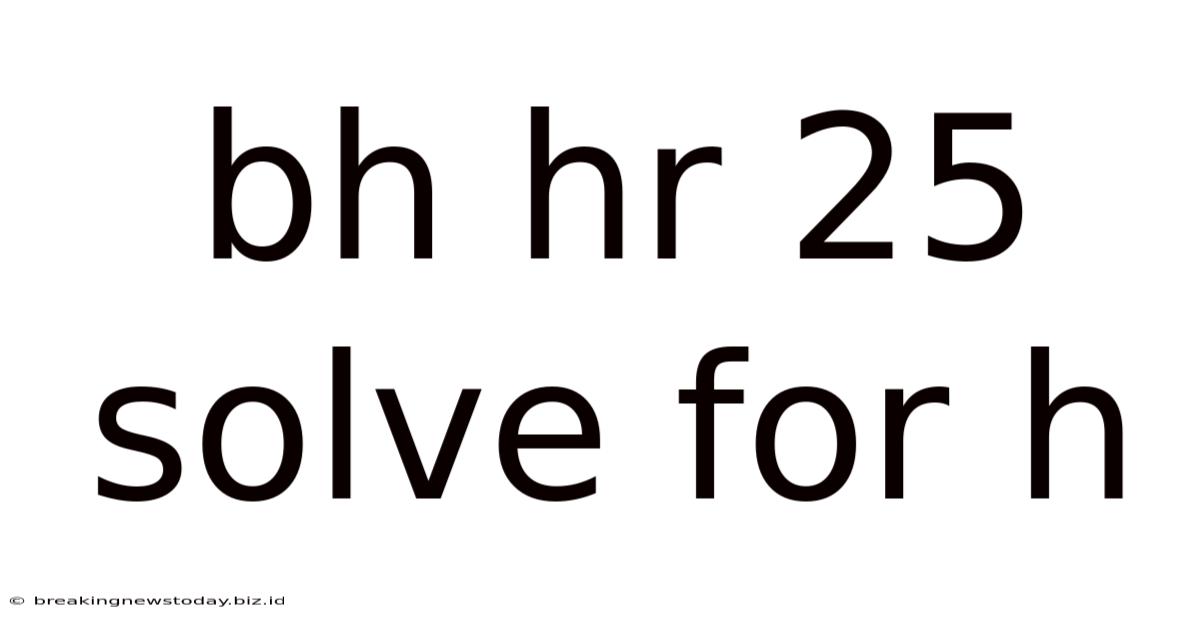
Table of Contents
Solving for 'h' in bh + hr = 25: A Comprehensive Guide
This article provides a detailed explanation of how to solve for the variable 'h' in the equation bh + hr = 25. We'll cover various scenarios, including the presence of known and unknown values for 'b' and 'r', and demonstrate different algebraic techniques to achieve the solution. This comprehensive guide will equip you with the skills to tackle similar algebraic problems effectively.
Understanding the Equation: bh + hr = 25
The equation bh + hr = 25 represents a linear equation with two variables, 'h' and 'r' (assuming 'b' is another variable or a constant). The goal is to isolate 'h' on one side of the equation, expressing it in terms of 'b' and 'r'. This process is fundamental in algebra and frequently applied in various fields, including physics, engineering, and finance.
Key Concepts:
- Variables: 'b', 'h', and 'r' are variables, meaning they can represent different numerical values.
- Constants: 25 is a constant; its value remains unchanged.
- Solving for a Variable: The objective is to manipulate the equation to isolate 'h' on one side, leaving an expression for 'h' in terms of 'b' and 'r' on the other.
Method 1: Factoring Out 'h'
This is the most efficient method for solving this type of equation. We can factor out 'h' from the left-hand side of the equation:
h(b + r) = 25
Now, to isolate 'h', we divide both sides of the equation by (b + r):
h = 25 / (b + r)
Important Consideration: This solution is valid only if (b + r) is not equal to zero. If (b + r) = 0, the equation becomes undefined, as division by zero is not allowed in mathematics.
Method 2: Expanding and Rearranging (Less Efficient)
While factoring is the preferred method, we can also solve the equation by expanding and rearranging terms. However, this method is less efficient and prone to errors, especially with more complex equations.
- Assume values for 'b' and 'r': To illustrate, let's assume b = 2 and r = 3. Substitute these values into the original equation:
2h + 3h = 25
- Combine like terms:
5h = 25
- Solve for 'h':
h = 25 / 5 = 5
This method works well when specific values are given for 'b' and 'r'. However, it doesn't provide a general solution for 'h' in terms of 'b' and 'r', unlike the factoring method.
Scenario 1: 'b' and 'r' are Known Constants
If 'b' and 'r' are known constants, the solution becomes straightforward. Simply substitute their values into the equation:
h = 25 / (b + r)
For example:
If b = 3 and r = 7:
h = 25 / (3 + 7) = 25 / 10 = 2.5
If b = 1 and r = 4:
h = 25 / (1 + 4) = 25 / 5 = 5
Scenario 2: 'b' and/or 'r' are Unknown Variables
If 'b' and/or 'r' are unknown variables, the solution for 'h' will remain an algebraic expression in terms of these variables:
h = 25 / (b + r)
This expression represents the general solution for 'h' when 'b' and 'r' are not specified. To obtain a numerical value for 'h', you would need to substitute the known values for 'b' and 'r'.
Scenario 3: Applications in Geometry and Other Fields
This equation, though seemingly simple, finds applications in various fields. For instance, it might represent the area of a composite shape. Imagine a composite shape formed by two rectangles. 'b' could represent the width of one rectangle, 'r' the width of the other, and 'h' their shared height. The total area (25) would then be the sum of the areas of the two rectangles.
In such contexts, solving for 'h' would help determine the height based on the known or measurable widths and total area. Similarly, the equation could represent aspects of physics, financial modeling, or other fields where the relationship between variables is additive and linear.
Error Handling and Common Mistakes
- Division by Zero: The most common mistake is not considering the condition (b + r) ≠ 0. Always check if the denominator is zero before calculating the value of 'h'.
- Incorrect Order of Operations: Remember to follow the order of operations (PEMDAS/BODMAS). Parentheses/Brackets must be evaluated first.
- Algebraic Errors: Carefully perform the algebraic manipulations to avoid errors in factoring, combining like terms, or dividing.
Advanced Considerations: Systems of Equations
In more complex scenarios, the equation bh + hr = 25 might be part of a system of equations with additional equations involving 'b', 'h', and 'r'. Solving such a system requires techniques like substitution, elimination, or matrix methods, depending on the nature of the additional equations.
For example, if we had another equation like b = 2r, we could substitute this expression for 'b' into the original equation, resulting in a new equation with only 'h' and 'r'. Further manipulation could then lead to the solution for both 'h' and 'r'.
Conclusion: Mastering the Fundamentals
Solving for 'h' in the equation bh + hr = 25 is a fundamental algebraic skill. By mastering the techniques outlined in this article, including factoring and careful algebraic manipulation, you can confidently solve this and similar equations. Remember to always check for division by zero and carefully evaluate the order of operations to avoid errors. Understanding the various scenarios, including cases where 'b' and 'r' are constants or variables, will enhance your problem-solving capabilities in algebra and its applications in various fields. The ability to derive the general solution for 'h' demonstrates a deeper understanding of algebraic manipulation and sets a solid foundation for tackling more complex mathematical problems.
Latest Posts
Latest Posts
-
What Is The Rhyme Scheme Of Interflora Poem
Jun 06, 2025
-
200 96 Rounded To The Nearest Hundredth
Jun 06, 2025
-
Determine The Following Quantities For The Circuit Shown Below
Jun 06, 2025
-
Which Of The Following Statements Best Defines Lanthionization
Jun 06, 2025
-
Congruent Triangles Worksheet B Answers Math Giraffe
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Bh Hr 25 Solve For H . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.