Break Apart The Second Addend To Find 56+38
Breaking News Today
Jun 07, 2025 · 5 min read
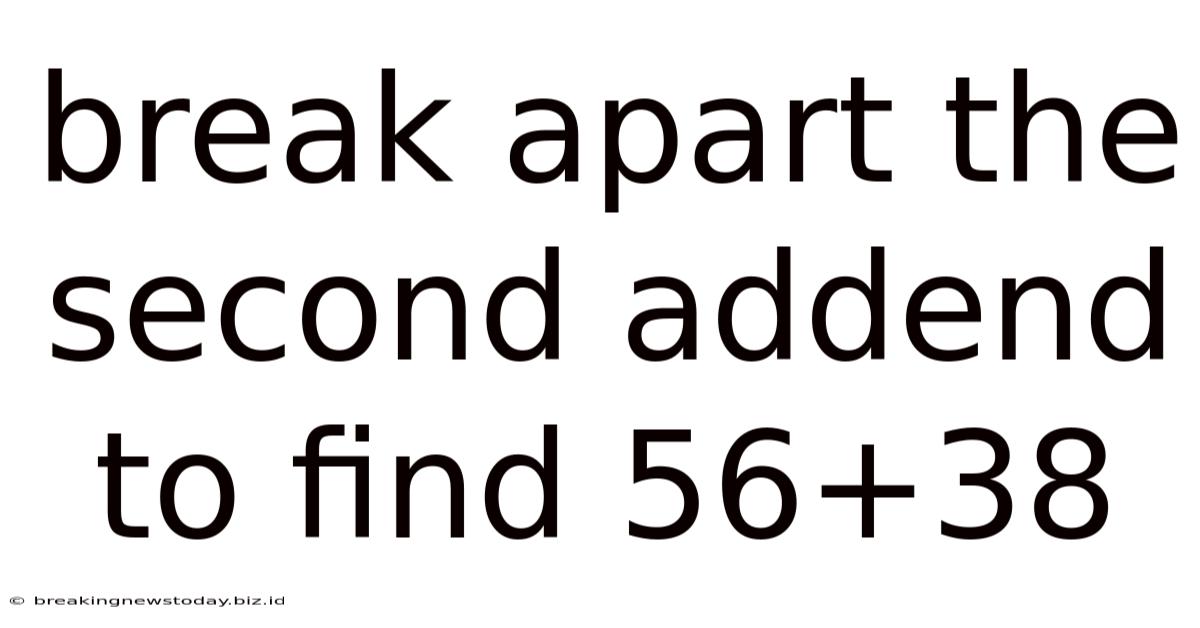
Table of Contents
Breaking Apart the Second Addend: Mastering Addition Strategies for 56 + 38
Adding numbers efficiently is a fundamental skill in mathematics. While simple addition problems can be solved through direct counting, more complex additions require strategic approaches. One such powerful technique is breaking apart the second addend. This method simplifies calculations, making it easier to solve problems like 56 + 38 and build a stronger understanding of number sense. This comprehensive guide will explore this technique in detail, providing examples and exercises to solidify your understanding.
Understanding the Concept of Breaking Apart
Breaking apart, also known as decomposition, is a mental math strategy where you split a number into smaller, more manageable parts. In the context of addition, this involves separating one of the addends (the numbers being added) into tens and ones or other convenient parts to simplify the overall calculation. For the problem 56 + 38, we'll focus on breaking apart the second addend, 38.
Why Break Apart the Second Addend?
Breaking apart the second addend is particularly useful because it allows us to leverage the existing value of the first addend. By strategically breaking down the second number, we can create easier additions that ultimately lead to the same result. This method helps students develop a deeper understanding of place value and the properties of addition, such as the associative property (grouping numbers differently doesn't change the sum).
Breaking Apart 38 in 56 + 38: A Step-by-Step Guide
Let's delve into the process of solving 56 + 38 using the breaking apart method. We'll decompose 38 into its tens and ones: 30 and 8.
Step 1: Decompose the Second Addend
We'll break apart 38 into 30 and 8. This is a natural decomposition based on place value.
Step 2: Add the Tens
Now, add the tens from the second addend to the first addend: 56 + 30. This is a relatively straightforward addition:
56 + 30 = 86
Step 3: Add the Ones
Next, add the ones from the second addend to the result from Step 2: 86 + 8. This is a simpler addition than the original problem:
86 + 8 = 94
Step 4: Final Result
The final sum is 94. Therefore, 56 + 38 = 94.
Visualizing the Process: Using Models
Visual aids can significantly improve understanding, especially for younger learners. Several models can be used to represent the breaking apart method:
1. Base Ten Blocks
Imagine using base ten blocks. Represent 56 with 5 tens and 6 ones. Then, represent 38 with 3 tens and 8 ones. Combine the tens and ones separately, then combine the results. This visually demonstrates the concept of regrouping and adding place values independently.
2. Number Lines
A number line can also illustrate the process. Start at 56. Move 30 units to the right (adding 30). Then, move another 8 units to the right (adding 8). The final position on the number line represents the sum (94).
3. Area Models
An area model can visually represent the breakdown. Draw a rectangle and divide it into sections representing the decomposed numbers. Label the sections accordingly and add the areas to find the total.
Variations in Breaking Apart: Flexibility and Adaptability
While breaking down into tens and ones is the most common approach, the beauty of this method lies in its flexibility. You can adapt the decomposition to suit the numbers involved. For example, you could break 38 into 20 and 18, or even 10 and 28, if it simplifies the addition further. The goal is to make the calculations as easy as possible.
Example using a different decomposition:
Let's break 38 into 20 and 18:
- 56 + 20 = 76 (Adding the tens)
- 76 + 18 = 94 (Adding the remaining ones)
The result remains the same, highlighting the flexibility of this method.
Beyond 56 + 38: Applying the Strategy to Other Problems
The breaking apart strategy isn't limited to 56 + 38. It's a versatile technique applicable to various addition problems. Here are a few examples:
- 72 + 29: Break 29 into 20 and 9. 72 + 20 = 92; 92 + 9 = 101.
- 45 + 67: Break 67 into 60 and 7. 45 + 60 = 105; 105 + 7 = 112.
- 134 + 88: Break 88 into 80 and 8. 134 + 80 = 214; 214 + 8 = 222.
This method proves particularly helpful with larger numbers, making them more manageable and less prone to errors.
Building Number Sense and Mental Math Skills
The breaking apart method is more than just a trick to solve addition problems; it’s a powerful tool for developing crucial mathematical skills:
- Place Value Understanding: This method reinforces the understanding of place value and how tens and ones contribute to the overall value of a number.
- Mental Math Proficiency: Regular practice with this technique enhances mental math skills, making calculations faster and more efficient.
- Number Flexibility: It promotes flexibility in thinking about numbers and finding different ways to approach a problem.
- Problem-Solving Skills: It encourages strategic thinking and problem-solving by breaking down complex problems into simpler steps.
Practice Problems
Here are some practice problems to help you master the breaking apart method:
- 83 + 47
- 61 + 59
- 125 + 76
- 99 + 35
- 152 + 68
Remember to break apart the second addend strategically to simplify the calculation. Try different ways of breaking apart the numbers to discover the most efficient approach for each problem.
Conclusion: Mastering Addition through Strategic Decomposition
The breaking apart method, specifically focusing on decomposing the second addend, is a valuable addition strategy. It simplifies complex addition problems, making them more accessible and improving mathematical understanding. By regularly practicing this technique and employing visual models, students can develop strong number sense, enhance mental math abilities, and build a solid foundation for more advanced mathematical concepts. The flexibility of the method makes it a versatile tool adaptable to various addition problems, empowering learners with a powerful problem-solving skill. Remember, the key is to choose a decomposition that makes the subsequent additions as straightforward as possible. Through consistent practice and a focus on understanding the underlying principles, you can truly master this valuable addition strategy.
Latest Posts
Latest Posts
-
Which Words Share The Same Word Root Select Three Options
Jun 07, 2025
-
Insert The Protech Presentation Outline Docx
Jun 07, 2025
-
Identify An Accurate Statement About Cap Wigs
Jun 07, 2025
-
Which Phrase Describes A Contour Interval
Jun 07, 2025
-
How Many Chemical Changes Occurred In This Scenario
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Break Apart The Second Addend To Find 56+38 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.