C 85x 60 Solve For X
Breaking News Today
Jun 04, 2025 · 6 min read
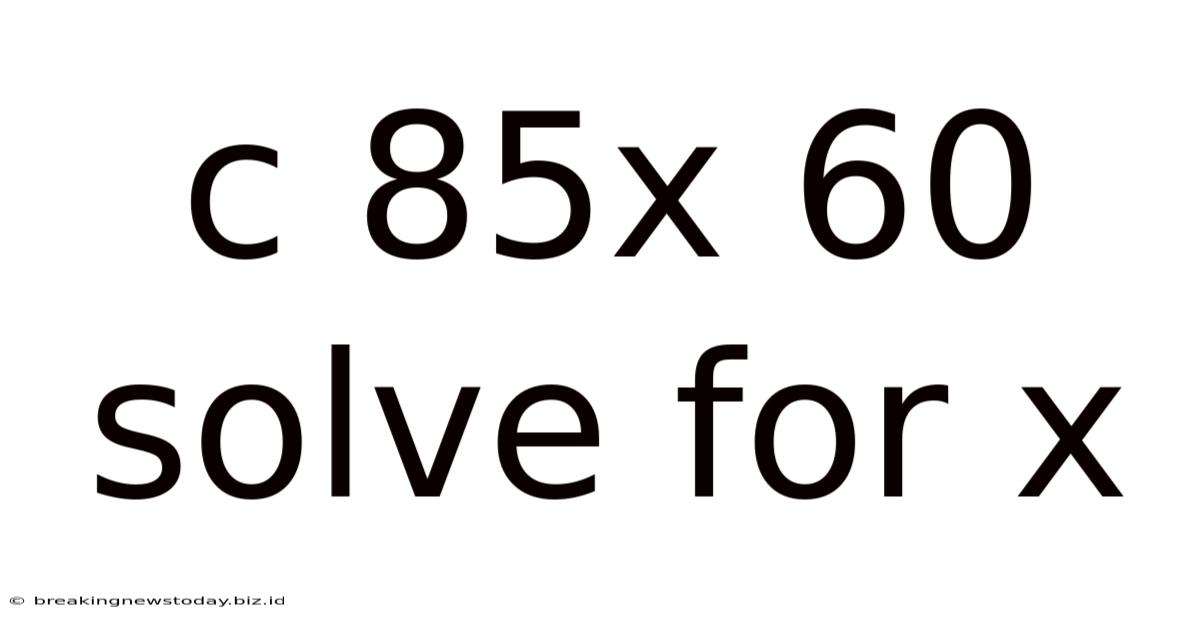
Table of Contents
Solving for x: A Comprehensive Guide to C = 85x + 60
This article provides a comprehensive guide on how to solve for 'x' in the equation C = 85x + 60. We'll explore various methods, delve into the underlying mathematical concepts, and offer practical examples to solidify your understanding. Whether you're a student tackling algebra problems or a professional needing to solve for a variable in a real-world application, this guide will equip you with the necessary knowledge and skills.
Understanding the Equation: C = 85x + 60
Before we jump into solving for 'x', let's first understand the equation itself. This is a linear equation, meaning it represents a straight line when graphed. The equation shows a relationship between two variables, 'C' and 'x', where:
- C: Represents the total cost (or any dependent variable). This is the value that depends on the value of 'x'.
- x: Represents a quantity, number of units, or any independent variable. This is the value that can be changed to affect 'C'.
- 85: Represents the cost per unit of 'x' (or the slope of the line). This is the constant rate of change.
- 60: Represents a fixed cost (or the y-intercept). This is a constant value that is added regardless of the value of 'x'.
Therefore, the equation C = 85x + 60 states that the total cost (C) is calculated by multiplying the number of units ('x') by the cost per unit (85) and then adding a fixed cost of 60.
Method 1: Solving for x using Algebraic Manipulation
This is the most common and straightforward method. To solve for 'x', we need to isolate 'x' on one side of the equation. Here's a step-by-step guide:
-
Start with the equation: C = 85x + 60
-
Subtract 60 from both sides: C - 60 = 85x
-
Divide both sides by 85: (C - 60) / 85 = x
-
Therefore, the solution is: x = (C - 60) / 85
This formula allows you to calculate the value of 'x' for any given value of 'C'.
Method 2: Using a Graphical Approach
While algebraic manipulation is precise, a graphical approach can provide a visual understanding of the solution. You can plot the equation C = 85x + 60 on a graph with 'x' on the horizontal axis and 'C' on the vertical axis.
-
Identify the y-intercept: The y-intercept is the point where the line crosses the vertical axis (when x = 0). In this case, it's 60.
-
Determine the slope: The slope is the rate of change of 'C' with respect to 'x'. The slope is 85, meaning for every one-unit increase in 'x', 'C' increases by 85.
-
Plot the line: Using the y-intercept and slope, plot the line on the graph.
-
Solve for x: To find the value of 'x' for a given value of 'C', locate the point on the line corresponding to that 'C' value. The x-coordinate of that point represents the solution for 'x'.
This method provides a visual representation of the relationship between 'C' and 'x', which can be helpful for understanding the problem context. However, it's less precise than algebraic manipulation, particularly for large values or complex equations.
Method 3: Utilizing Numerical Methods (For Specific C values)
If you have a specific value for 'C', you can directly substitute it into the equation and solve for 'x'. This is a simple and effective method for specific scenarios.
Example: Let's say C = 550. Substitute this value into the equation:
550 = 85x + 60
Now solve for x:
-
Subtract 60 from both sides: 490 = 85x
-
Divide both sides by 85: x = 490 / 85 = 5.76 (approximately)
This method is efficient for finding 'x' for individual 'C' values, but it doesn't provide a general solution like the algebraic manipulation method.
Practical Applications and Real-World Scenarios
The equation C = 85x + 60 can model numerous real-world situations. Here are a few examples:
-
Cost of Production: Imagine a company manufacturing widgets. The fixed cost (60) could represent rent, utilities, and salaries. The cost per unit (85) represents the raw materials and labor involved in producing each widget. 'x' represents the number of widgets produced, and 'C' represents the total cost of production.
-
Pricing Strategy: A business might use this equation to determine their pricing strategy. The fixed cost might include marketing and advertising expenses. The cost per unit represents the production cost of the product or service. 'x' could be the number of units sold and 'C' represents the revenue needed to cover costs and make a profit.
-
Financial Modeling: This equation could represent a simple financial model where 'x' represents the number of investments, 85 the return on each investment, and 60 represents initial investment costs. 'C' represents total return on the investment portfolio.
Understanding how to solve for 'x' in this equation allows businesses and individuals to make informed decisions based on cost analysis, pricing, and financial projections.
Advanced Considerations and Extensions
While we've focused on the basic solution, there are several advanced considerations:
-
Negative Values: What if 'x' or 'C' results in a negative value? In real-world applications, negative values might not always be meaningful. For instance, a negative number of widgets produced isn't physically possible. The context of the problem determines the interpretation of negative values.
-
Multiple Variables: The equation could be extended to include more variables. For example, C = 85x + 60 + 10y, where 'y' could represent another cost factor. Solving this equation would require additional steps.
-
Non-Linear Equations: The equation C = 85x + 60 is a linear equation. However, real-world scenarios might involve non-linear relationships, requiring more advanced mathematical techniques to solve.
-
Error Analysis: When working with real-world data, there will be measurement errors. Understanding how these errors propagate through the calculation and impact the accuracy of the solution is crucial.
Conclusion: Mastering the Solution to C = 85x + 60
Solving for 'x' in the equation C = 85x + 60 is a fundamental skill in algebra and has wide-ranging applications in various fields. By understanding the underlying principles and applying the methods discussed—algebraic manipulation, graphical representation, and numerical methods—you can effectively solve this equation and similar linear equations, contributing to informed decision-making in diverse contexts. Remember to consider the practical implications of your solutions and adapt your approach based on the specific context of the problem. Through consistent practice and a solid understanding of the underlying mathematical concepts, you can confidently tackle this type of equation and expand your problem-solving abilities.
Latest Posts
Latest Posts
-
Composers Choose Instrument Combinations When Orchestrating A Piece
Jun 06, 2025
-
0 001 Is 1 10 Of What Number
Jun 06, 2025
-
Use The Bootstrap Distributions In Figure 1
Jun 06, 2025
-
A Ship Sails At 15 Miles Per Hour
Jun 06, 2025
-
Which Of The Following Statements Describes Data Interoperability
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about C 85x 60 Solve For X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.