Choose The Graph Of Y 3x 1
Breaking News Today
Jun 07, 2025 · 5 min read
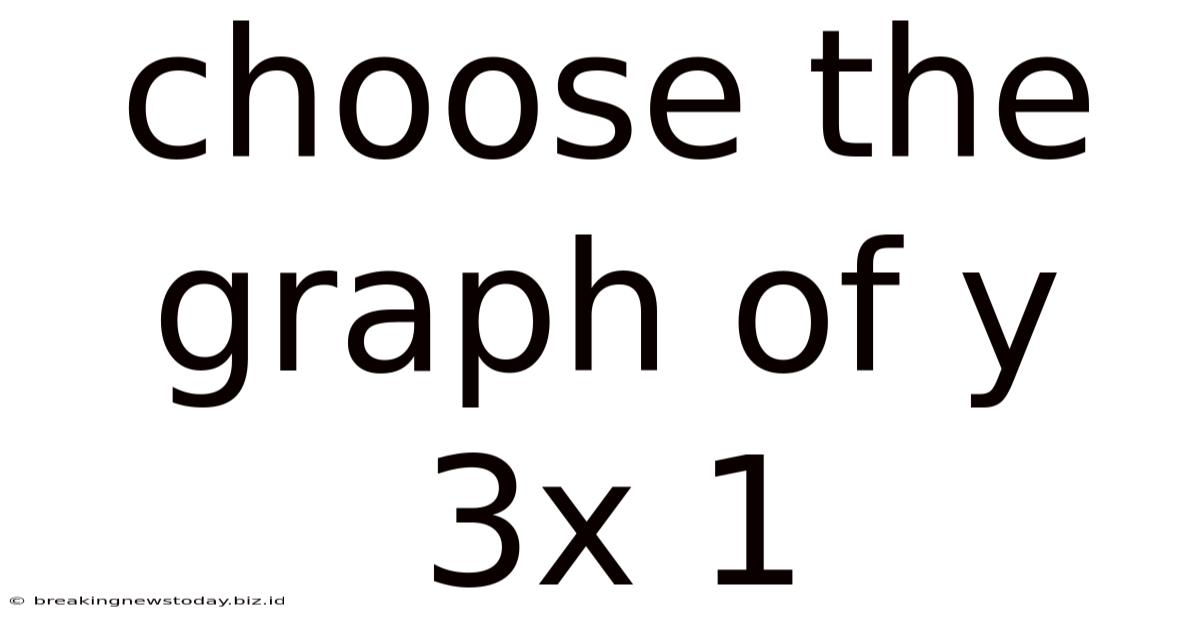
Table of Contents
Choosing the Graph of y = 3x + 1: A Comprehensive Guide
Understanding linear equations and their graphical representations is fundamental to algebra and numerous applications in various fields. This comprehensive guide delves into the process of choosing the correct graph for the equation y = 3x + 1, explaining the underlying principles and providing a step-by-step approach to confidently identify the correct visual representation. We'll explore different methods, emphasizing conceptual understanding and practical application.
Understanding the Equation y = 3x + 1
The equation y = 3x + 1 represents a linear relationship between two variables, x and y. This is because the highest power of x is 1. This type of equation is in the slope-intercept form, which is written as:
y = mx + b
where:
- m represents the slope of the line (the steepness of the line). A positive slope indicates an upward trend from left to right, while a negative slope indicates a downward trend.
- b represents the y-intercept (the point where the line crosses the y-axis, i.e., where x = 0).
In our equation, y = 3x + 1:
- m = 3: This means the line has a slope of 3. For every one unit increase in x, y increases by three units. A slope of 3 indicates a relatively steep positive slope.
- b = 1: This means the line intersects the y-axis at the point (0, 1).
Methods to Identify the Correct Graph
Several methods can help you choose the correct graph for y = 3x + 1. Let's explore the most common and effective approaches:
1. Using the Slope and Y-intercept
This is the most direct method. Since we know the slope (m = 3) and the y-intercept (b = 1), we can directly look for a graph that:
- Crosses the y-axis at 1: The line must pass through the point (0, 1).
- Has a positive slope of 3: The line should incline upwards from left to right, and a rise of 3 units should correspond to a run of 1 unit. This can be visualized as moving 1 unit to the right and 3 units up from any point on the line.
By examining the provided graphs, eliminate any graphs that don't satisfy these two conditions.
2. Plotting Points
Another reliable method is to plot several points that satisfy the equation and then connect them to form the line. Let's choose a few values for x and calculate the corresponding y values:
| x | y = 3x + 1 | (x, y) coordinates |
|---|---|---|
| -1 | -2 | (-1, -2) |
| 0 | 1 | (0, 1) |
| 1 | 4 | (1, 4) |
| 2 | 7 | (2, 7) |
Plot these points (-1, -2), (0, 1), (1, 4), and (2, 7) on a coordinate plane. Connecting these points should result in a straight line that represents the equation y = 3x + 1. Compare this line to the graphs provided. The graph that accurately represents these plotted points is the correct graph.
3. Using the Equation to Check Points on the Graph
If you're given multiple graphs, you can select a point from each graph and substitute its x and y coordinates into the equation y = 3x + 1. If the equation holds true for the point, then the graph containing that point is a potential candidate. Let’s illustrate:
Suppose Graph A shows a line passing through (1, 4). Substituting x = 1 and y = 4 into the equation:
4 = 3(1) + 1
4 = 4
The equation holds true. Graph A could be the correct graph (but we need to check other points or conditions to be certain).
Suppose Graph B shows a line passing through (2, 5). Substituting x = 2 and y = 5 into the equation:
5 = 3(2) + 1
5 = 7
The equation is false. Therefore, Graph B is incorrect.
Continue this process for all provided graphs, checking multiple points from each to eliminate incorrect options. Remember, one incorrect point is enough to disqualify a graph.
4. Understanding the Implications of Slope and Intercept
The slope (3) and y-intercept (1) provide crucial information about the line’s characteristics:
- Positive Slope: This indicates a line that rises from left to right. The larger the positive slope, the steeper the line.
- Y-intercept of 1: The line intersects the y-axis at the point (0,1).
By analyzing the graphical representation, ensure the visual matches these characteristics. A line with a negative slope, a different y-intercept, or a different steepness cannot represent the equation y = 3x + 1.
Avoiding Common Mistakes
When choosing the correct graph, be mindful of these common pitfalls:
- Misinterpreting the slope: Ensure you accurately understand the rise over run relationship of the slope. A slope of 3 means a rise of 3 units for every 1 unit run. Do not confuse this with other ratios.
- Neglecting the y-intercept: The y-intercept is a crucial point that helps pinpoint the line's position. Ignoring it can lead to selecting the wrong graph.
- Relying solely on visual estimation: While visual inspection can provide a preliminary assessment, don't rely solely on it. Use algebraic methods (plotting points or using the equation to check points) for verification.
Practical Applications and Real-World Examples
The equation y = 3x + 1, and the skill of interpreting its graph, has numerous practical applications in various fields. A few examples include:
- Economics: Representing the relationship between price (y) and quantity (x) in a linear supply or demand model.
- Physics: Describing the relationship between distance (y) and time (x) in a uniformly accelerated motion.
- Engineering: Modeling linear relationships between different variables in design and analysis.
- Finance: Illustrating the growth of an investment over time, where the slope represents the rate of return.
Mastering the ability to accurately interpret linear equations and their graphical representations is crucial for effective problem-solving in these and other fields.
Conclusion
Choosing the correct graph for the equation y = 3x + 1 requires a thorough understanding of the slope-intercept form of a linear equation. By employing the methods outlined in this guide—using the slope and y-intercept, plotting points, checking points against the equation, and understanding the implications of slope and intercept—you can confidently identify the correct graphical representation and apply this crucial skill to various real-world problems. Practice is key; the more you work with linear equations and their graphs, the more intuitive the process will become. Remember to check your work rigorously to avoid common errors and ensure accuracy.
Latest Posts
Latest Posts
-
Clauses Building And Refining Compound And Complex Sentences
Jun 07, 2025
-
Select All Steps Below That Help You Handle Chemicals Safely
Jun 07, 2025
-
Select All The Ways The Brain Can Grow
Jun 07, 2025
-
Why Was The Student Scared Of The Average Teacher
Jun 07, 2025
-
Who Applied Assembly Line Techniques To Home Construction In The 1950s
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Choose The Graph Of Y 3x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.