Choose The Inverse Of Y X2 10x
Breaking News Today
Jun 06, 2025 · 5 min read
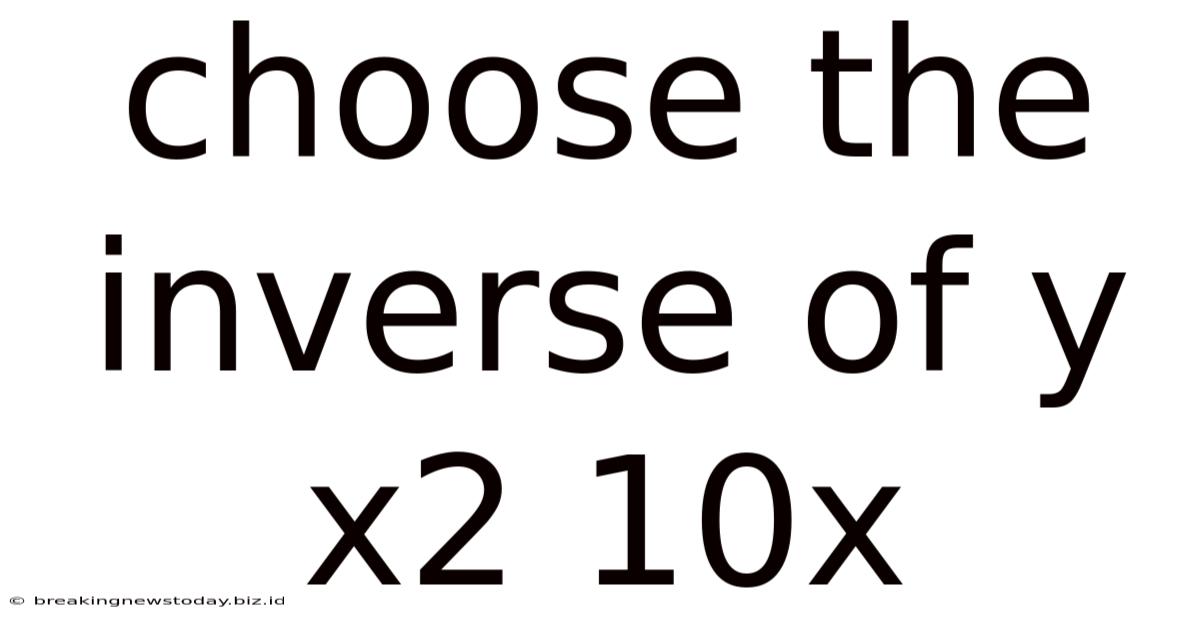
Table of Contents
Choosing the Inverse of y = x² + 10x
Finding the inverse of a function is a fundamental concept in algebra and calculus. It involves switching the roles of the independent and dependent variables (typically x and y) and then solving for the new dependent variable. However, not all functions have an inverse that is also a function. This is particularly true for quadratic functions like y = x² + 10x, which are not one-to-one. Let's explore this in detail, examining different approaches and understanding the implications.
Understanding Inverse Functions
Before diving into the specifics of inverting y = x² + 10x, let's review the core idea of inverse functions. A function, simply put, is a relationship where each input (x) corresponds to exactly one output (y). An inverse function, denoted as f⁻¹(x), "undoes" the original function. In other words, if f(a) = b, then f⁻¹(b) = a. Graphically, the inverse function is a reflection of the original function across the line y = x.
Key characteristics of inverse functions:
-
One-to-one correspondence: For a function to have an inverse that's also a function, it must be one-to-one. This means each output (y) corresponds to exactly one input (x). If a horizontal line intersects the graph of the function more than once, the function is not one-to-one and does not have a true inverse function.
-
Domain and Range: The domain of the original function becomes the range of its inverse, and vice versa.
-
Composition: The composition of a function and its inverse results in the identity function, meaning f(f⁻¹(x)) = x and f⁻¹(f(x)) = x.
Why y = x² + 10x Doesn't Have a Simple Inverse Function
The function y = x² + 10x is a quadratic function, and its graph is a parabola. Parabolas fail the horizontal line test; a horizontal line will intersect the parabola at two points (except at the vertex). This means the function is not one-to-one, therefore it does not have an inverse function that is itself a function over its entire domain.
To illustrate, consider the points (1, 11) and (-11, 11) on the graph of y = x² + 10x. Both have the same y-value, demonstrating the many-to-one nature of the function. This means a single output (y) corresponds to multiple inputs (x), violating the condition for a function to have an inverse function.
Finding a Partial Inverse: Restricting the Domain
While a full inverse function doesn't exist for y = x² + 10x, we can find a partial inverse by restricting the domain of the original function. This means we'll consider only a portion of the parabola where it is one-to-one.
Let's follow these steps:
- Complete the square: Rewrite the quadratic equation in vertex form to identify the vertex. y = x² + 10x y = (x² + 10x + 25) - 25 y = (x + 5)² - 25
The vertex of the parabola is (-5, -25).
-
Restrict the domain: To make the function one-to-one, we can restrict the domain to either x ≥ -5 (the right half of the parabola) or x ≤ -5 (the left half). Let's choose x ≥ -5.
-
Find the inverse: Now, we can find the inverse for this restricted domain:
a) Swap x and y: x = (y + 5)² - 25 b) Solve for y: x + 25 = (y + 5)² ±√(x + 25) = y + 5 y = -5 ± √(x + 25)
Since we restricted the domain to x ≥ -5, we choose the positive square root to ensure the inverse function's range corresponds to the restricted domain:
y = -5 + √(x + 25)
This is the inverse function for the restricted domain x ≥ -5. It's important to remember that this is only a partial inverse; it doesn't apply to the entire original function.
Graphical Representation and Verification
The graph of the original function y = x² + 10x and its partial inverse y = -5 + √(x + 25) will be reflections of each other across the line y = x, but only within the restricted domain. Outside of this restricted domain, the relationship doesn't hold. You can use graphing software or a calculator to visualize this reflection.
Applications and Further Considerations
Understanding the limitations of inverting quadratic functions is crucial in various applications, including:
-
Optimization problems: Quadratic functions are often used to model optimization problems. Finding the inverse might be needed to analyze the relationship between variables but needs careful consideration of the domain.
-
Transformations: Understanding inverse functions is essential in understanding transformations and their effects on functions.
-
Calculus: Finding inverses is a key step in certain calculus problems. For example, finding the inverse function is crucial to calculate the inverse function theorem which has many implications in calculus and differential equations.
-
Solving equations: The inverse function can help in solving equations involving the original function.
Conclusion: The Importance of Domain Restriction
The example of y = x² + 10x clearly demonstrates that not all functions have a simple, universally applicable inverse function. The concept of restricting the domain is vital for finding partial inverses which are, in a limited context, suitable replacements for the true inverse. Understanding the limitations and implications of domain restriction is crucial for correctly applying inverse functions in various mathematical and real-world contexts. Always be mindful of the original function's characteristics and the resulting consequences of domain restrictions when dealing with the inverse. Careful consideration is paramount to avoid misinterpretations and ensure accurate results. The process of finding the inverse of a function provides a deeper understanding of the function's properties and behaviors and the critical relationship between a function and its inverse.
Latest Posts
Latest Posts
-
Who Applied Assembly Line Techniques To Home Construction In The 1950s
Jun 07, 2025
-
Choose The Two Graphs That Preserve Congruence
Jun 07, 2025
-
The Following Diagram Illustrates Kohlbergs Stages Of Moral Development
Jun 07, 2025
-
In This Excerpt What Does Exquisite Mean
Jun 07, 2025
-
Partially Thawed Torn Packages Of Frozen Steaks
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Choose The Inverse Of Y X2 10x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.