Completely Factor The Expression 18x2 - 78x - 60.
Breaking News Today
Jun 04, 2025 · 5 min read
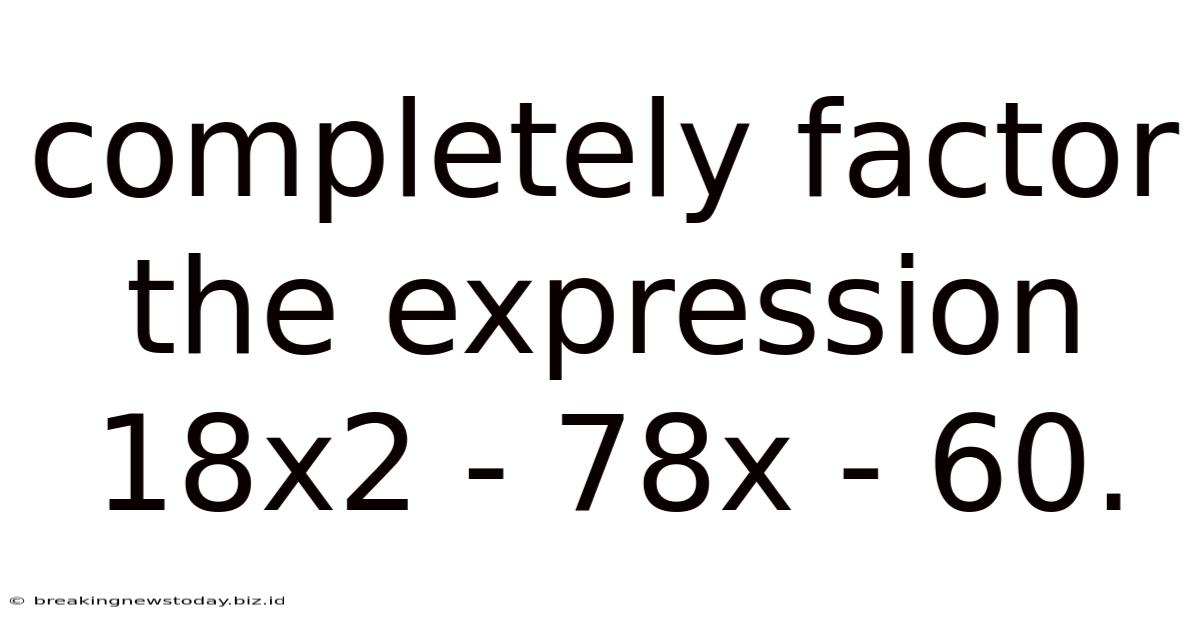
Table of Contents
Completely Factor the Expression 18x² - 78x - 60: A Comprehensive Guide
Factoring expressions is a fundamental skill in algebra, crucial for solving equations, simplifying expressions, and understanding mathematical relationships. This article delves into the complete factorization of the expression 18x² - 78x - 60, providing a step-by-step approach and exploring various techniques applicable to similar problems. We will not only find the factored form but also explore the underlying concepts and strategies that empower you to tackle more complex factoring challenges.
Understanding the Problem: 18x² - 78x - 60
Before we begin the factorization, let's understand the structure of the expression. We have a quadratic trinomial, meaning it's a polynomial with three terms, and the highest power of the variable (x) is 2. The goal is to rewrite this expression as a product of simpler expressions, ideally linear factors (expressions of the form ax + b). This process reverses the expansion of products using the distributive property (often called FOIL).
Step 1: Finding the Greatest Common Factor (GCF)
The first and often most important step in factoring any polynomial is to identify the greatest common factor (GCF) of all its terms. This simplifies the expression and makes subsequent factoring steps easier. Let's examine the coefficients of our expression: 18, -78, and -60.
What is the greatest common divisor of 18, 78, and 60? We can find this by determining the prime factorization of each number:
- 18 = 2 x 3²
- 78 = 2 x 3 x 13
- 60 = 2² x 3 x 5
The common factors are 2 and 3. Therefore, the GCF is 2 x 3 = 6.
Now, we factor out the GCF from the expression:
18x² - 78x - 60 = 6(3x² - 13x - 10)
This already simplifies our problem considerably. We now need to factor the quadratic trinomial inside the parentheses.
Step 2: Factoring the Quadratic Trinomial (3x² - 13x - 10)
Factoring a quadratic trinomial of the form ax² + bx + c can be approached in several ways. We will explore two common methods: the ac method and trial and error.
Method 1: The ac Method
This method systematically finds factors that satisfy the conditions of the quadratic.
-
Multiply a and c: In our case, a = 3 and c = -10, so a * c = -30.
-
Find factors of ac that add up to b: We need two numbers that multiply to -30 and add up to -13 (our b value). These numbers are -15 and 2.
-
Rewrite the middle term: We rewrite -13x as -15x + 2x:
3x² - 15x + 2x - 10
-
Factor by grouping: We group the terms in pairs and factor out the GCF from each pair:
3x(x - 5) + 2(x - 5)
-
Factor out the common binomial factor: Notice that (x - 5) is common to both terms. We factor it out:
(x - 5)(3x + 2)
Method 2: Trial and Error
This method involves directly testing different combinations of binomial factors until we find the one that expands to the original trinomial. It relies on understanding how the coefficients in the binomials interact during expansion.
We are looking for two binomials of the form (ax + b)(cx + d) where a * c = 3 and b * d = -10. We also need to ensure that the outer and inner terms add up to -13x. After trying different combinations, we arrive at:
(x - 5)(3x + 2)
This gives us the same result as the ac method.
Step 3: Combining the Factors
Now that we have factored the quadratic trinomial, we can combine it with the GCF we factored out earlier:
18x² - 78x - 60 = 6(3x² - 13x - 10) = 6(x - 5)(3x + 2)
This is the completely factored form of the expression.
Verifying the Factorization
To ensure our factorization is correct, we can expand the factored form using the distributive property (FOIL):
6(x - 5)(3x + 2) = 6(3x² + 2x - 15x - 10) = 6(3x² - 13x - 10) = 18x² - 78x - 60
This confirms that our factorization is accurate.
Applications of Factoring
Factoring quadratic expressions, like the one we just solved, is a fundamental skill in algebra with numerous applications:
-
Solving Quadratic Equations: By setting the factored expression equal to zero, we can solve for the values of x that make the equation true. This is essential in various fields, including physics, engineering, and economics.
-
Simplifying Rational Expressions: Factoring is crucial for simplifying rational expressions (fractions with polynomials in the numerator and denominator). This makes it easier to work with and manipulate these expressions.
-
Graphing Quadratic Functions: The factored form reveals the x-intercepts (roots) of a quadratic function, which are essential points for accurately graphing the parabola. These intercepts represent the values of x where the function equals zero.
-
Calculus: Factoring plays a crucial role in many calculus techniques, particularly in finding derivatives and integrals.
Advanced Factoring Techniques
While the ac method and trial and error work well for many quadratic trinomials, more complex polynomials may require advanced techniques like:
-
Substitution: This involves substituting a simpler variable for a more complex expression to simplify the factoring process.
-
Grouping: As seen in the ac method, grouping terms can reveal common factors leading to factorization.
-
Difference of Squares: This formula, a² - b² = (a + b)(a - b), is useful for factoring expressions where two perfect squares are subtracted.
-
Sum and Difference of Cubes: Similar to the difference of squares, formulas exist for factoring the sum and difference of cubes.
Conclusion
Completely factoring the expression 18x² - 78x - 60, which resulted in 6(x - 5)(3x + 2), highlights the importance of mastering factoring techniques. The step-by-step approach, using the GCF and the ac method (or trial and error), provides a robust strategy for tackling similar problems. Remember that practicing various factoring techniques will solidify your understanding and improve your problem-solving skills in algebra and beyond. Understanding factoring is not just about manipulating symbols; it's about understanding the underlying mathematical structure and relationships, skills vital for success in advanced mathematical studies and various scientific and engineering fields. The ability to effortlessly factor expressions unlocks a deeper understanding of algebraic concepts and empowers you to solve more complex problems with confidence.
Latest Posts
Latest Posts
-
A Young Work Crew Is Trying To Quickly Finish
Jun 06, 2025
-
When Installing A Campus Backbone System Avoid The Use Of
Jun 06, 2025
-
Sydney Drew A Flow Chart To Illustrate The Nitrogen Cycle
Jun 06, 2025
-
Write 2 49 100 As A Decimal Number
Jun 06, 2025
-
A Botanist Collected One Leaf At Random
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Completely Factor The Expression 18x2 - 78x - 60. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.