Completely Factor The Polynomial 8x2 24x 20x 60
Breaking News Today
Jun 05, 2025 · 4 min read
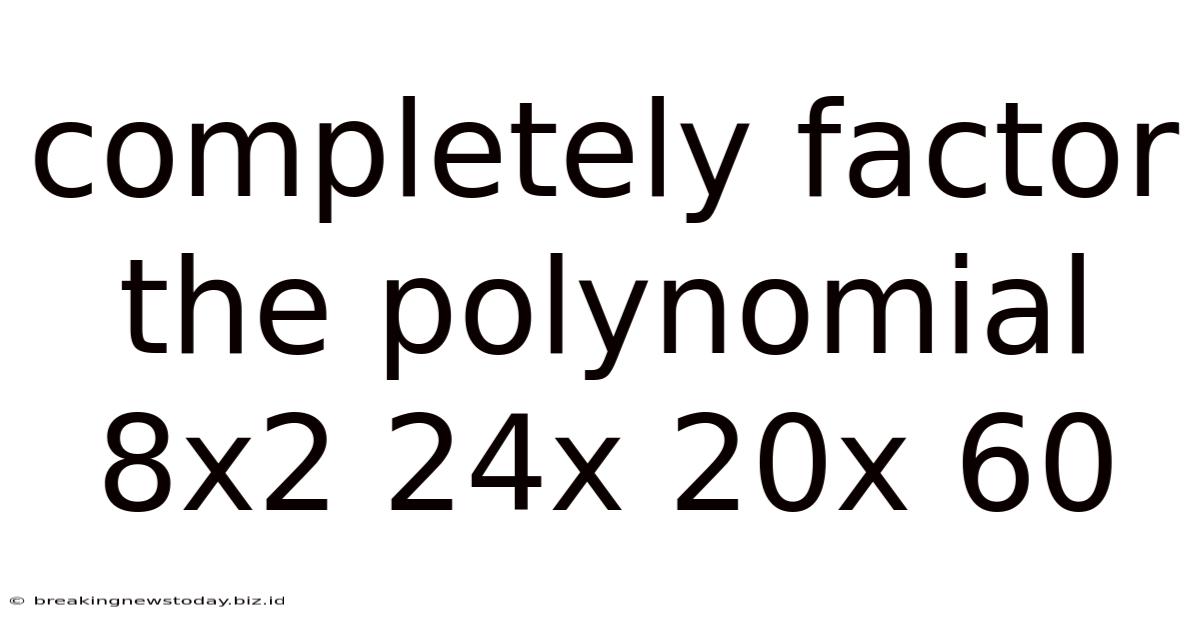
Table of Contents
Completely Factoring the Polynomial 8x² + 24x + 20x + 60
This article delves into the complete factorization of the polynomial 8x² + 24x + 20x + 60, exploring various factoring techniques and demonstrating a step-by-step solution. We will cover fundamental algebraic concepts and advanced strategies to ensure a comprehensive understanding of polynomial factorization. Understanding this process is crucial for success in algebra, calculus, and other advanced mathematical fields.
Understanding Polynomial Factorization
Polynomial factorization involves expressing a polynomial as a product of simpler polynomials. It's the reverse process of polynomial expansion (using the distributive property). Factoring simplifies complex polynomials, making them easier to analyze and manipulate. This is fundamental in solving equations, simplifying expressions, and understanding the behavior of functions. In this case, our polynomial is 8x² + 24x + 20x + 60.
The Importance of Factoring
The ability to factor polynomials is a cornerstone of algebra. Its applications extend across numerous mathematical domains:
- Solving Polynomial Equations: Factoring allows us to find the roots (solutions) of polynomial equations. Setting the factored polynomial equal to zero and solving for x provides the roots.
- Simplifying Expressions: Factoring reduces complex polynomial expressions to simpler forms, making them easier to understand and work with.
- Calculus: Factoring is crucial in calculus for finding derivatives, integrals, and limits.
- Graphing Polynomials: The factored form of a polynomial reveals important information about its graph, such as x-intercepts.
Step-by-Step Factorization of 8x² + 24x + 20x + 60
Our polynomial is 8x² + 24x + 20x + 60. Notice that we can simplify this by combining like terms:
8x² + 44x + 60
Now, let's factor this simplified polynomial. We'll employ a combination of techniques:
1. Greatest Common Factor (GCF)
The first step in factoring any polynomial is to identify the greatest common factor (GCF) among all the terms. In our case, all terms are divisible by 2. Therefore, we can factor out a 2:
2(4x² + 22x + 30)
2. Factoring the Quadratic Expression
We're left with a quadratic expression inside the parentheses: 4x² + 22x + 30. This can be factored further. There are several methods to factor quadratic expressions:
- Trial and Error: This involves finding two binomials whose product equals the quadratic.
- AC Method: This method is systematic and generally more reliable for complex quadratics.
- Quadratic Formula: This formula provides the roots directly, which can then be used to factor the quadratic.
Let's use the AC method:
a = 4, b = 22, c = 30
- Multiply a and c: 4 * 30 = 120
- Find two numbers that add up to b (22) and multiply to 120: These numbers are 12 and 10.
- Rewrite the middle term (22x) using these two numbers: 4x² + 12x + 10x + 30
- Factor by grouping: Group the terms in pairs and factor out the GCF from each pair:
- (4x² + 12x) + (10x + 30)
- 4x(x + 3) + 10(x + 3)
- Factor out the common binomial (x + 3): (4x + 10)(x + 3)
Now, let's substitute this back into our original factored expression:
2(4x + 10)(x + 3)
3. Further Simplification
Notice that (4x + 10) has a GCF of 2. We can factor this out:
2 * 2(2x + 5)(x + 3)
4. Final Factored Form
Finally, we simplify the expression to get the completely factored form:
4(2x + 5)(x + 3)
Therefore, the complete factorization of 8x² + 24x + 20x + 60 is 4(2x + 5)(x + 3).
Verifying the Factorization
To verify our factorization, we can expand the factored form:
4(2x + 5)(x + 3) = 4(2x² + 6x + 5x + 15) = 4(2x² + 11x + 15) = 8x² + 44x + 60
This matches our simplified original polynomial, confirming the accuracy of our factorization.
Advanced Factoring Techniques
While the AC method and trial and error are effective for many quadratics, more advanced techniques are needed for higher-degree polynomials or those with complex coefficients. These include:
- Synthetic Division: This method is useful for dividing polynomials by linear factors. It can help find roots and subsequently factor the polynomial.
- Rational Root Theorem: This theorem helps identify potential rational roots of a polynomial, which can then be used to find factors.
- Difference of Squares: This technique applies to expressions of the form a² - b², which factors to (a + b)(a - b).
- Sum and Difference of Cubes: Similar to the difference of squares, this applies to expressions of the form a³ + b³ and a³ - b³.
Applications of Polynomial Factoring
Beyond its use in simplifying expressions and solving equations, polynomial factoring finds applications in diverse fields:
- Engineering: In structural engineering, polynomial functions are used to model stress and strain, and factoring helps simplify these models.
- Computer Science: Polynomial factoring is integral to algorithm design and cryptography.
- Economics: Polynomial functions are used in economic modeling, and factoring can simplify these models.
- Physics: Polynomial functions describe various physical phenomena, and factoring helps in their analysis.
Conclusion
Factoring the polynomial 8x² + 24x + 20x + 60 involves a systematic approach combining the identification of the greatest common factor with efficient methods for factoring quadratic expressions. The final completely factored form is 4(2x + 5)(x + 3). Mastering polynomial factorization is a critical skill that provides a solid foundation for further studies in mathematics and its applications across various disciplines. By understanding and applying these techniques, you can effectively solve polynomial equations, simplify complex expressions, and gain deeper insights into the behavior of polynomial functions. Remember to always check your work by expanding the factored form to ensure it matches the original polynomial.
Latest Posts
Latest Posts
-
In Cell D15 Enter A Formula
Jun 06, 2025
-
Which Of The Following Accurately Describes Properties Of Valence
Jun 06, 2025
-
What Does Mrs Morningstar Suggest That Sancho Should Get
Jun 06, 2025
-
What Does The Audible Tone In Most Digital Ohmmeters Indicate
Jun 06, 2025
-
I Am A Number Less Than 40
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Completely Factor The Polynomial 8x2 24x 20x 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.