D 4n 2 Solve For N
Breaking News Today
Jun 02, 2025 · 5 min read
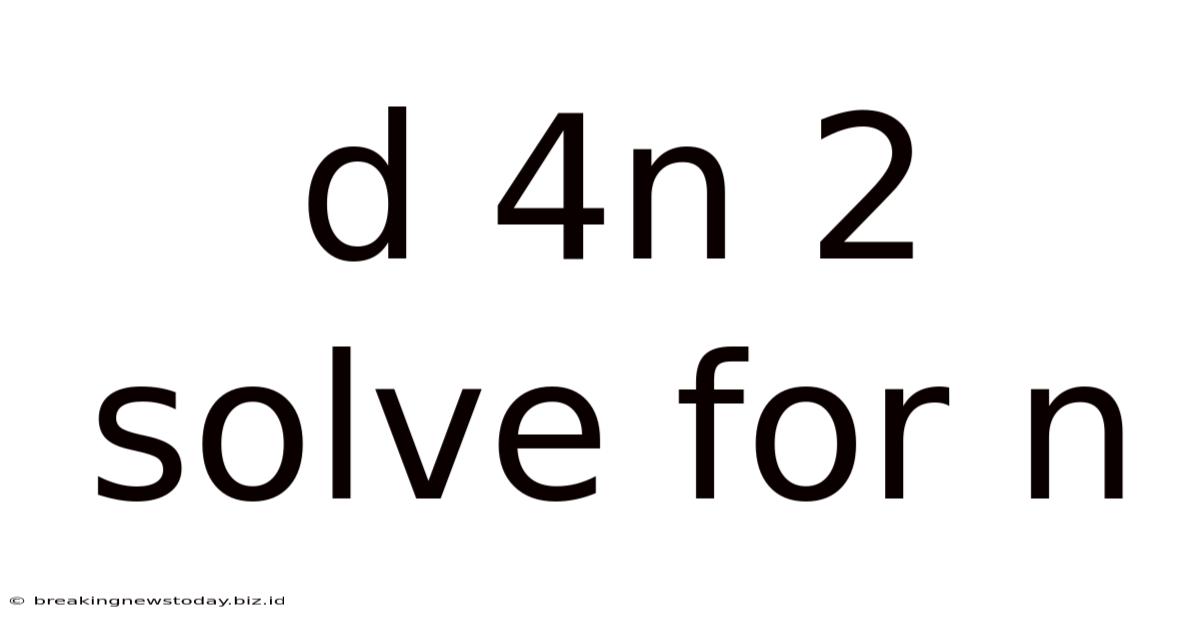
Table of Contents
Solving for 'n': A Deep Dive into the Equation d = 4n
This article provides a comprehensive guide to understanding and solving the equation d = 4n, exploring various approaches, applications, and extensions. We'll delve into the mathematical concepts, offer practical examples, and discuss how to adapt this foundational equation to more complex scenarios. Understanding this simple equation is crucial for building a strong foundation in algebra and its numerous applications.
Understanding the Equation: d = 4n
The equation d = 4n represents a direct proportional relationship between two variables, 'd' and 'n'. This means that as 'n' increases, 'd' increases proportionally, and vice-versa. 'd' is dependent on 'n', meaning its value is directly determined by the value of 'n'. The constant '4' represents the constant of proportionality – it indicates that 'd' is always four times the value of 'n'.
Key Terminology:
- Variable: A symbol (like 'd' or 'n') representing a quantity that can vary.
- Constant: A fixed value (like '4' in this equation).
- Equation: A mathematical statement that shows the equality of two expressions.
- Direct Proportion: A relationship where two variables change at the same rate.
Solving for 'n'
The primary focus of this article is solving for 'n', given a value for 'd'. This involves isolating 'n' on one side of the equation. To do this, we employ basic algebraic manipulation:
1. Dividing Both Sides by 4:
Since 'n' is multiplied by 4, the inverse operation – division – is used to isolate 'n'. We divide both sides of the equation by 4:
d / 4 = (4n) / 4
This simplifies to:
n = d / 4
This is the solution for 'n'. It means that to find the value of 'n', you simply divide the value of 'd' by 4.
Practical Applications and Examples
The equation d = 4n and its solution, n = d/4, have numerous applications across various fields. Let's examine a few examples:
Example 1: Calculating the Number of Items
Imagine you're buying apples that come in bags of 4. 'd' represents the total number of apples, and 'n' represents the number of bags. If you have 20 apples (d = 20), how many bags did you buy?
Using the formula: n = d / 4 = 20 / 4 = 5 bags.
Example 2: Determining Distance Traveled
Suppose a car travels at a constant speed of 4 miles per hour. 'd' represents the total distance traveled (in miles), and 'n' represents the number of hours. If the car traveled 16 miles (d = 16), how many hours did it take?
Using the formula: n = d / 4 = 16 / 4 = 4 hours.
Example 3: Calculating Unit Cost
A pack of 4 pencils costs a certain amount. 'd' represents the total cost, and 'n' represents the cost of a single pencil. If the pack costs $8 (d = 8), what is the cost of one pencil?
Using the formula: n = d / 4 = 8 / 4 = $2 per pencil.
Extending the Equation: Introducing More Variables
While d = 4n is a simple equation, understanding its principles allows us to tackle more complex problems. Let's introduce a new variable and explore how to solve for 'n' in a modified scenario.
Let's say the equation becomes:
d = 4n + c
Where 'c' represents a constant value added to the equation. This could represent a fixed cost, an initial value, or any other constant addition.
To solve for 'n', we follow these steps:
- Subtract 'c' from both sides: d - c = 4n
- Divide both sides by 4: (d - c) / 4 = n
Therefore, the solution for 'n' in this extended equation is:
n = (d - c) / 4
This demonstrates the adaptability of the basic equation to accommodate additional factors.
Real-World Applications in Different Fields
The principles underlying the equation d = 4n are applicable across a wide range of disciplines:
- Engineering: Calculating material quantities, determining dimensions, and solving for unknown variables in simple systems.
- Physics: Solving basic motion problems, analyzing simple circuits, and working with directly proportional relationships between physical quantities.
- Finance: Calculating simple interest, determining unit costs, and solving for unknown variables in basic financial models.
- Business: Calculating inventory, determining production rates, and projecting sales based on simple proportional relationships.
- Computer Science: Working with algorithms, managing data structures, and solving simple programming problems.
Troubleshooting Common Mistakes
When solving for 'n' in equations like d = 4n or its variations, some common mistakes can arise:
- Incorrect Order of Operations: Remember to follow the order of operations (PEMDAS/BODMAS) – Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
- Errors in Algebraic Manipulation: Carefully check each step of your algebraic manipulations. A small mistake in adding, subtracting, multiplying, or dividing can lead to an incorrect solution.
- Misinterpreting the Equation: Ensure you understand the meaning of each variable and the relationship between them before attempting to solve the equation.
Advanced Concepts and Further Exploration
While this article focuses on the basic equation d = 4n, the principles discussed can be extrapolated to more complex algebraic equations and systems of equations. Understanding this foundation is crucial for tackling more challenging mathematical problems in the future.
Further exploration might include:
- Solving systems of equations: Involving multiple equations with multiple variables.
- Graphing linear equations: Visualizing the relationship between 'd' and 'n'.
- Working with inequalities: Exploring scenarios where 'd' might be greater than or less than 4n.
- Introducing exponents and logarithmic functions: Expanding the mathematical complexity of the problem.
Conclusion
The seemingly simple equation d = 4n, and its solution for 'n', serves as a fundamental building block in mathematics and its countless applications. Mastering the ability to solve for 'n' in this equation and its variations provides a solid base for tackling more intricate mathematical problems across various fields. By understanding the underlying principles, practicing various examples, and recognizing potential pitfalls, you can confidently approach and solve a wide array of equations and real-world problems. This foundational knowledge is invaluable for anyone seeking to enhance their mathematical skills and problem-solving abilities.
Latest Posts
Latest Posts
-
If Were In Pistol With 2 Wr To The Left
Jun 04, 2025
-
A Loan For A Motorcycle Is An Example Of
Jun 04, 2025
-
What Is The Measure Of 4
Jun 04, 2025
-
The Graph Shows The Cube Root Parent Function
Jun 04, 2025
-
An Image Created By Defining Points And Curves
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about D 4n 2 Solve For N . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.