Eight Minus The Square Of A Number
Breaking News Today
Jun 06, 2025 · 5 min read
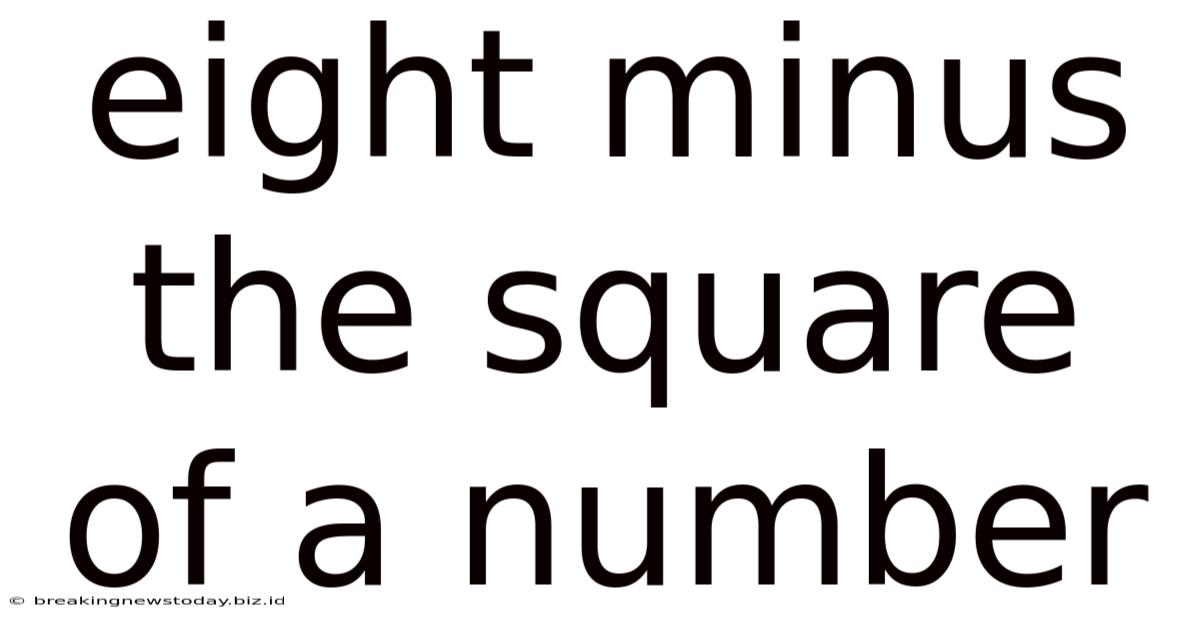
Table of Contents
Eight Minus the Square of a Number: A Deep Dive into Mathematical Expressions
The seemingly simple phrase "eight minus the square of a number" hides a world of mathematical richness. This seemingly basic algebraic expression opens doors to exploring various concepts, including quadratic equations, their solutions, graphical representations, and real-world applications. This article delves into this expression, exploring its various facets and uncovering the fascinating mathematical landscape it unveils.
Understanding the Expression: 8 - x²
At its core, the expression "eight minus the square of a number" translates directly into the algebraic equation: 8 - x². Here:
- 8 represents the constant value eight.
- x represents the unknown number (a variable).
- x² represents the square of the number, meaning the number multiplied by itself (x * x).
- - denotes subtraction.
This simple equation forms the basis for a plethora of mathematical investigations.
Exploring the Quadratic Nature
The presence of the x² term signifies that we are dealing with a quadratic equation. Quadratic equations are polynomial equations of the second degree, meaning the highest power of the variable is 2. Their general form is ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. In our case, a = -1, b = 0, and c = 8. The equation can be rewritten as:
-x² + 8 = 0 or equivalently x² - 8 = 0
This seemingly minor rearrangement allows us to readily apply established methods for solving quadratic equations.
Solving the Equation: Finding the Roots
Solving a quadratic equation means finding the values of 'x' that satisfy the equation. There are several methods to achieve this:
-
Factoring: While not always directly applicable, factoring can be a quick method for simple quadratic equations. In this case, we can rewrite the equation as:
(x - √8)(x + √8) = 0
This gives us two solutions:
- x = √8 = 2√2 (approximately 2.828)
- x = -√8 = -2√2 (approximately -2.828)
-
Quadratic Formula: This is a universal method for solving any quadratic equation. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
Substituting our values (a = -1, b = 0, c = 8), we get:
x = ± √(0² - 4 * -1 * 8) / (2 * -1)
This simplifies to the same solutions we obtained through factoring: x = ±2√2.
-
Completing the Square: This method involves manipulating the equation to create a perfect square trinomial. While less straightforward in this particular example, completing the square is a valuable technique for solving more complex quadratic equations.
Graphical Representation: Visualizing the Solution
The expression 8 - x² can be represented graphically as a parabola. Parabolas are symmetrical U-shaped curves. In this case, because the coefficient of x² is negative (-1), the parabola opens downwards.
The roots of the equation (the solutions we found: ±2√2) are the x-intercepts of the parabola – the points where the curve intersects the x-axis (where y = 0). The y-intercept (where x = 0) is 8, representing the value of the expression when x is zero.
Plotting this parabola provides a visual understanding of the relationship between x and the expression's value. The graph clearly shows that the expression is positive between the two roots and negative elsewhere. This visual representation provides a deeper intuitive grasp of the equation's behavior.
Real-World Applications: Beyond the Abstract
While seemingly abstract, the expression "eight minus the square of a number" has practical implications in various fields:
Physics: Projectile Motion
In physics, particularly in projectile motion calculations, quadratic equations are frequently used to model the trajectory of an object under the influence of gravity. The height (y) of a projectile as a function of time (t) often follows a parabolic path, similar to our expression. Analyzing such equations is crucial for determining things like maximum height reached and the time of flight.
Engineering: Designing Structures
Engineers utilize quadratic equations when designing various structures, such as bridges and buildings. Understanding the behavior of quadratic expressions is essential for ensuring structural stability and safety under different loads and conditions. The curvature of structures, for example, can be mathematically described by quadratic functions.
Economics: Maximizing Profit
In economics, quadratic functions can model profit functions. Businesses often aim to find the optimal production level (x) that maximizes their profit (y). This often involves solving quadratic equations to identify the peak of a parabolic profit function.
Computer Graphics: Creating Curves
Quadratic equations play a significant role in computer graphics and animation. They are used to generate smooth curves and represent various shapes. Understanding quadratic functions allows for precise control over the shapes and trajectories of objects in computer-generated images and animations.
Extending the Concept: Variations and Generalizations
We can expand on the basic expression "8 - x²" by introducing further complexity:
-
Adding a linear term: Consider the expression 8 - x² + 3x. This becomes a more general quadratic equation requiring the more complete methods (quadratic formula or completing the square) for solving. The graphical representation will still be a parabola but with a shifted vertex.
-
Changing the constant: Replacing '8' with another constant changes the y-intercept and shifts the parabola vertically. The roots, however, will also change, altering the points where the parabola intersects the x-axis.
-
Introducing a coefficient for x²: Expressions like 5(8 - x²) or -2x² + 8 introduce scaling and reflection transformations on the parabola, changing its shape and the location of the roots.
Conclusion: The Enduring Significance of 8 - x²
The simple expression "eight minus the square of a number" serves as a powerful entry point into the fascinating world of quadratic equations. From its basic algebraic representation to its graphical interpretation and diverse real-world applications, this expression underscores the importance of understanding quadratic functions in various scientific and technological fields. Its seemingly simple nature belies the depth and breadth of mathematical concepts that it unlocks, highlighting the interconnectedness of mathematical ideas and their relevance in solving real-world problems. Exploring this expression – and its many variations – offers a rewarding journey into the heart of algebra and beyond.
Latest Posts
Latest Posts
-
What Is Grendels Perspective On The Mens Fighting
Jun 06, 2025
-
All Internet Reference Pages Contain True And Credible Information
Jun 06, 2025
-
Which Expression Shows This Number In Expanded Form 0 624
Jun 06, 2025
-
A Reliable Experiment Can Have 2 Or 3 Independent Variables
Jun 06, 2025
-
Which Ordered Pairs Make Both Inequalities True Select Two Options
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Eight Minus The Square Of A Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.