Eight More Than Four Times A Number Is 28
Breaking News Today
Jun 01, 2025 · 5 min read
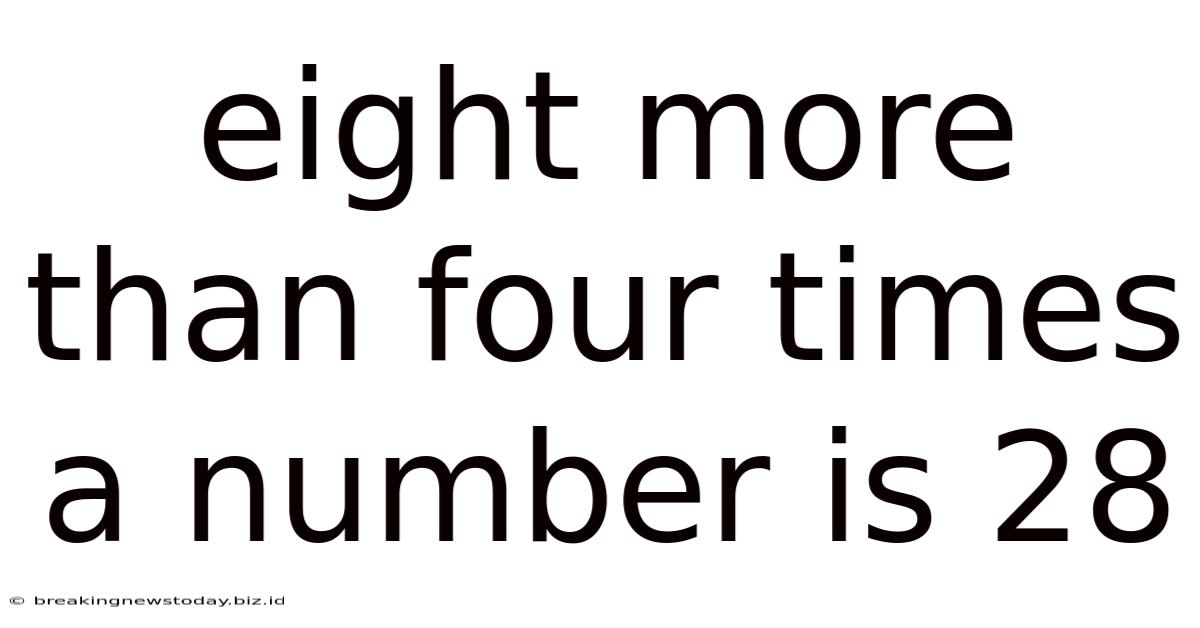
Table of Contents
Eight More Than Four Times a Number is 28: A Deep Dive into Problem-Solving
This seemingly simple math problem, "Eight more than four times a number is 28," offers a fantastic opportunity to explore several key mathematical concepts and problem-solving strategies. While the solution itself is straightforward, dissecting the problem reveals valuable insights applicable to more complex algebraic equations. This article will delve into solving the problem, explore different approaches, and discuss the broader implications of this type of problem in mathematics and real-world applications.
Understanding the Problem: Deconstructing the Sentence
Before diving into the solution, it's crucial to understand the language of the problem. The sentence, "Eight more than four times a number is 28," is essentially a word problem disguised as a simple algebraic equation. Let's break it down piece by piece:
- "a number": This represents an unknown value, which we typically denote with a variable, such as 'x' or 'n'.
- "four times a number": This translates to 4 * x (or 4n), representing multiplication.
- "Eight more than four times a number": This indicates addition. We're taking the result of "four times a number" and adding 8 to it, resulting in the expression 4x + 8 (or 4n + 8).
- "is 28": This signifies equality. The entire expression "eight more than four times a number" is equal to 28.
Therefore, the complete algebraic representation of the problem is: 4x + 8 = 28
Solving the Equation: A Step-by-Step Guide
Solving the equation 4x + 8 = 28 involves isolating the variable 'x' to find its value. We achieve this by applying inverse operations to both sides of the equation, maintaining balance. Here's a step-by-step approach:
-
Subtract 8 from both sides: This cancels out the +8 on the left side, leaving us with 4x = 20.
4x + 8 - 8 = 28 - 8 4x = 20 -
Divide both sides by 4: This isolates 'x', giving us the solution.
4x / 4 = 20 / 4 x = 5
Therefore, the number is 5. We can verify this solution by substituting 'x' with 5 in the original equation: 4(5) + 8 = 20 + 8 = 28. The equation holds true, confirming our solution.
Alternative Approaches: Exploring Different Methods
While the above method is the most straightforward, several alternative approaches can solve this equation. These alternative methods highlight the flexibility and interconnectedness of mathematical concepts:
1. Using Subtraction First:
Instead of subtracting 8 first, we could divide both sides by 4 initially:
(4x + 8) / 4 = 28 / 4
x + 2 = 7
x = 5
This method demonstrates that the order of operations can sometimes be adjusted, leading to the same result.
2. Graphical Representation:
We can represent the equation graphically by plotting the line y = 4x + 8 and finding the point where it intersects the line y = 28. The x-coordinate of this intersection point will be the solution. This method provides a visual representation of the solution and is particularly useful for understanding the relationship between algebraic equations and their graphical counterparts.
3. Using a Table of Values:
Creating a table of values for the equation y = 4x + 8 allows us to identify the value of x when y = 28. This method is useful for beginners and provides a concrete approach to understanding the equation's behavior.
| x | 4x + 8 | y |
|---|---|---|
| 0 | 8 | 8 |
| 1 | 12 | 12 |
| 2 | 16 | 16 |
| 3 | 20 | 20 |
| 4 | 24 | 24 |
| 5 | 28 | 28 |
| 6 | 32 | 32 |
Real-World Applications: Beyond the Classroom
This seemingly simple equation has numerous real-world applications. Consider these examples:
-
Calculating Costs: Imagine you're buying items that cost $4 each, and you have an additional $8 shipping fee. If your total cost is $28, how many items did you buy? This directly mirrors the problem we solved.
-
Determining Quantities in Recipes: If a recipe calls for four times a certain ingredient plus 8 grams of another, and the total weight is 28 grams, the equation can be used to calculate the quantity of the first ingredient.
-
Analyzing Sales Data: Businesses can use similar equations to analyze sales figures, determine profit margins, and forecast future sales based on various factors.
Extending the Concept: More Complex Equations
The principles applied to solve "Eight more than four times a number is 28" are fundamental to solving far more complex algebraic equations. The steps of isolating the variable through inverse operations remain crucial. Understanding this basic equation lays a strong foundation for tackling more challenging problems involving:
-
Multiple Variables: Equations with more than one unknown variable require more sophisticated techniques like substitution or elimination.
-
Exponents and Roots: Equations involving exponents or roots necessitate the use of logarithmic or exponential properties.
-
Inequalities: Instead of an equals sign, we might encounter inequalities (<, >, ≤, ≥), requiring different solution methods.
-
Systems of Equations: Solving multiple equations simultaneously to find the values of multiple variables.
Conclusion: A Foundation for Mathematical Understanding
The seemingly simple problem, "Eight more than four times a number is 28," serves as a powerful illustration of fundamental algebraic principles and problem-solving strategies. While the solution is straightforward, understanding the underlying concepts—variable representation, algebraic manipulation, and inverse operations—is crucial for success in more advanced mathematical studies. Furthermore, the ability to translate word problems into algebraic equations and apply these techniques to real-world scenarios is a valuable skill applicable across numerous disciplines and everyday situations. The journey from a simple sentence to a solved equation highlights the beauty and power of mathematics in its ability to model and solve problems in the world around us. Mastering this foundational concept unlocks a world of further mathematical exploration and problem-solving capabilities.
Latest Posts
Latest Posts
-
True Or False Schuberts Song Melodies Focused On Religious Themes
Jun 02, 2025
-
The Most Visible Indication Of Oversight Is The
Jun 02, 2025
-
Which Word From The Passage Is An Appeal To Pathos
Jun 02, 2025
-
If Moving With A Stream Of Vehicles Across A Railroad
Jun 02, 2025
-
Cut The Text At Your Local Homemade Warehouse
Jun 02, 2025
Related Post
Thank you for visiting our website which covers about Eight More Than Four Times A Number Is 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.