Estimate The Sum Of 196 And 482
Breaking News Today
Jun 08, 2025 · 5 min read
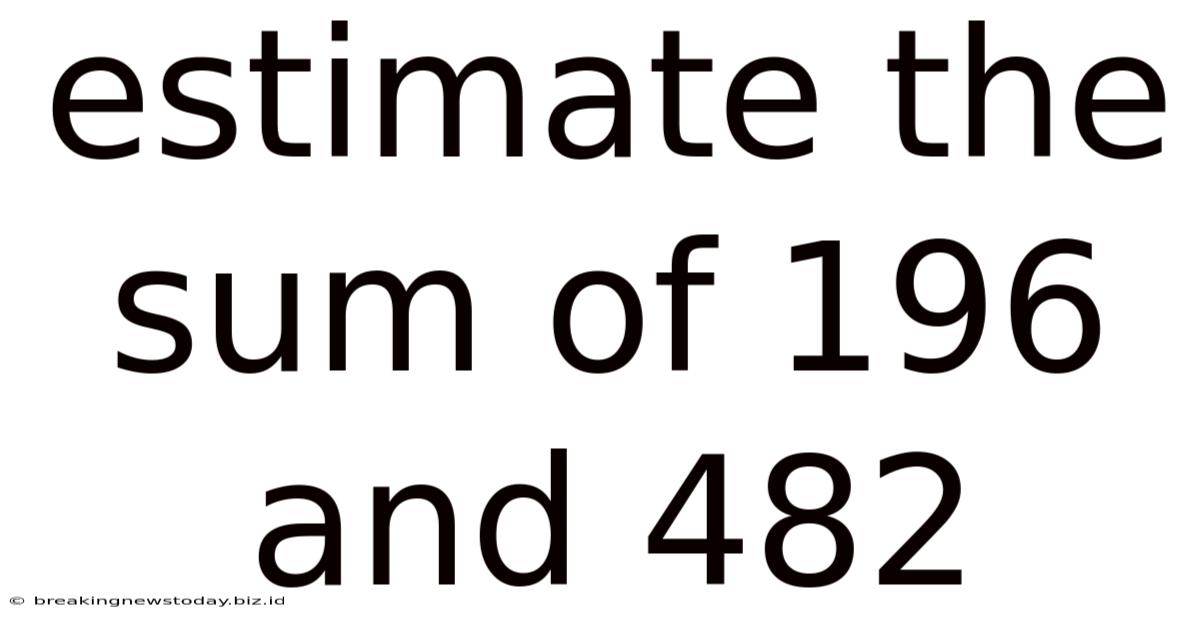
Table of Contents
Estimating the Sum of 196 and 482: A Deep Dive into Estimation Techniques
Estimating sums is a fundamental skill in mathematics, crucial not only for academic success but also for navigating everyday life. From quickly checking grocery bills to making rough calculations for large projects, the ability to accurately estimate can save time and prevent costly errors. This article will explore various methods for estimating the sum of 196 and 482, delving into the underlying principles and showcasing the practical applications of estimation techniques.
Understanding Estimation: Why It Matters
Before we dive into the specifics of estimating 196 + 482, let's establish the importance of estimation. Precise calculations are not always necessary, and often, a close approximation is sufficient. Estimation offers several key advantages:
-
Speed and Efficiency: Estimating allows for quick calculations, saving valuable time in situations where exactness isn't paramount.
-
Error Detection: Estimation serves as a powerful tool for checking the reasonableness of precise calculations. If your estimated sum differs significantly from your calculated sum, it suggests a potential error in your calculation.
-
Real-World Applicability: Estimation is widely used in various fields, including budgeting, financial planning, engineering, and even scientific research.
-
Mental Math Development: Regular practice with estimation sharpens mental math skills, improving your overall numerical fluency.
Methods for Estimating 196 + 482
Several techniques can be employed to estimate the sum of 196 and 482. We'll examine some of the most common and effective approaches:
1. Rounding to the Nearest Ten
This is a simple and widely used method. We round each number to the nearest ten before adding:
- 196 rounds to 200
- 482 rounds to 480
Adding the rounded numbers: 200 + 480 = 680
Therefore, our estimate using rounding to the nearest ten is 680. This method provides a reasonably accurate estimate, especially when dealing with larger numbers.
2. Rounding to the Nearest Hundred
This method provides a coarser estimate but is quicker. We round each number to the nearest hundred:
- 196 rounds to 200
- 482 rounds to 500
Adding the rounded numbers: 200 + 500 = 700
Our estimate using rounding to the nearest hundred is 700. This method is ideal when a less precise estimate is acceptable and speed is prioritized.
3. Front-End Estimation
This technique focuses on the leading digits of the numbers. We add the leading digits and then adjust the estimate based on the remaining digits:
- Leading digits: 1 + 4 = 5 (representing 500)
- Remaining digits: 96 + 82 ≈ 180 (approximated)
- Total estimate: 500 + 180 = 680
Our front-end estimate is 680. This method balances speed and accuracy, often providing a reasonably close approximation.
4. Compatible Numbers
This involves adjusting the numbers to create easier-to-add pairs. We look for numbers that "fit together" nicely:
- We can adjust 196 to 200. To maintain balance, we subtract 4 from 482, resulting in 478.
- Now we have 200 + 478 = 678
Our estimate using compatible numbers is 678. This method emphasizes mental agility and creative number manipulation.
5. Clustering (for Multiple Numbers – applicable to this example by extending it)
While primarily used for multiple numbers, clustering can be adapted here. Imagine we had several numbers close together. This technique involves finding the average of the numbers and multiplying it by the number of values. While not directly applicable to just two numbers, we can use it if we expand this problem.
Let's suppose we need to add 196, 482, and 205. We would cluster around an average value, for example 300 (a rough average). The estimate would be 300 x 3 = 900. This would illustrate how clustering offers a swift approximation when multiple numbers are involved.
Comparing Estimation Methods
Each estimation method offers a unique balance of speed and accuracy. Rounding to the nearest ten provides a good compromise between the two. Rounding to the nearest hundred is faster but less accurate. Front-end estimation offers a similar level of accuracy to rounding to the nearest ten, while compatible numbers allows for more flexibility and mental manipulation.
Exact Calculation and Error Analysis
Let's calculate the exact sum of 196 and 482:
196 + 482 = 678
Now, let's analyze the error of our estimations:
- Rounding to the Nearest Ten: Error = 680 - 678 = 2
- Rounding to the Nearest Hundred: Error = 700 - 678 = 22
- Front-End Estimation: Error = 680 - 678 = 2
- Compatible Numbers: Error = 678 - 678 = 0
The compatible numbers method produced the exact answer in this specific instance, showcasing its power when numbers are carefully manipulated.
Applications of Estimation in Real Life
The ability to estimate sums has numerous practical applications:
-
Grocery Shopping: Quickly estimating the total cost of groceries before reaching the checkout counter.
-
Budgeting: Approximating monthly expenses to ensure sufficient funds are available.
-
Project Management: Estimating the total cost and time required for completing a project.
-
Travel Planning: Estimating the total travel expenses for a trip.
-
Tip Calculation: Quickly estimating the appropriate tip amount in a restaurant.
-
Construction: Making approximate material estimations for construction projects.
-
Financial Analysis: Performing quick calculations for analyzing investment portfolios.
Conclusion: Mastering Estimation for Everyday Success
Estimating sums is a versatile and valuable skill that improves with practice. By mastering different estimation techniques, you gain speed and efficiency while reducing the likelihood of errors. The choice of method depends on the desired level of accuracy and the time available. Remember, the goal of estimation isn't perfect precision but a reasonable approximation that helps in decision-making and problem-solving. Regular practice with these techniques will enhance your numerical fluency and make you more confident in tackling real-world mathematical challenges. The examples provided, along with the analysis of error margins, demonstrate how different approaches can yield varying degrees of accuracy. Understanding these nuances will allow for a more informed selection of estimation methods, adapting them to specific scenarios for optimal results. Therefore, embrace estimation as a powerful tool for navigating the mathematical aspects of daily life.
Latest Posts
Latest Posts
-
10th Grade Mid Year Assessment Commonlit Answers
Jun 08, 2025
-
According To Your Textbook Inflection Refers To The
Jun 08, 2025
-
Jazz Was Partially A Product Of What Social Movement
Jun 08, 2025
-
4 03 Quiz Creating An American Mythology
Jun 08, 2025
-
Which Of The Following Is The Midsegment Of Abc
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about Estimate The Sum Of 196 And 482 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.