Evaluate 8 3e When E 2
Breaking News Today
Jun 07, 2025 · 4 min read
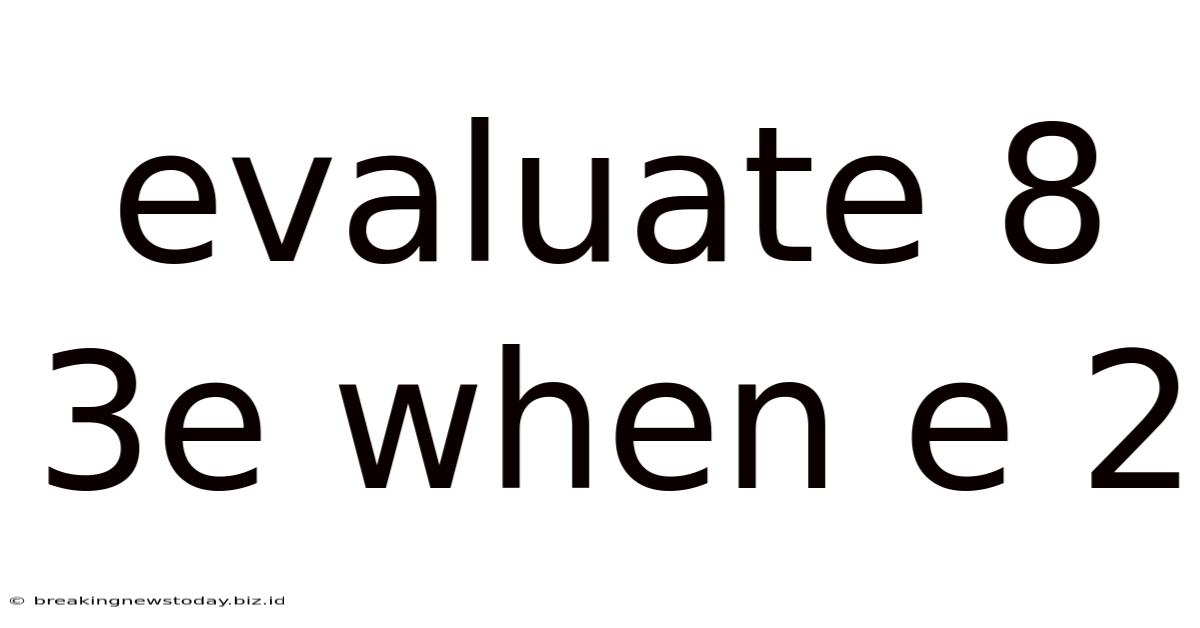
Table of Contents
Evaluating 8³e when e = 2: A Comprehensive Guide
This article delves into the mathematical evaluation of the expression 8³e when the variable 'e' is assigned the value 2. We will break down the problem step-by-step, explaining the order of operations, and exploring the underlying mathematical concepts involved. This will be a comprehensive guide suitable for anyone from high school students to those refreshing their mathematical skills. We'll also discuss the broader context of evaluating algebraic expressions and the importance of understanding the order of operations (PEMDAS/BODMAS).
Understanding the Expression: 8³e
The expression 8³e is an algebraic expression. It contains:
- A constant: 8
- An exponent: ³ (cubed, meaning raised to the power of 3)
- A variable: e
- Implicit multiplication: The absence of an explicit multiplication symbol (*) implies multiplication between 8³ and e.
The expression instructs us to:
- Cube the number 8 (calculate 8³).
- Multiply the result by the value of the variable 'e'.
Order of Operations: PEMDAS/BODMAS
Before we substitute the value of 'e', it is crucial to understand the order of operations. This ensures we calculate the expression correctly. The acronyms PEMDAS and BODMAS represent the same order, with slight variations in terminology:
- Parentheses/ Brackets
- Exponents/ Orders
- Multiplication and Division (from left to right)
- Addition and Subtraction (from left to right)
In our expression, 8³e, we first address the exponent (8³) before performing the multiplication.
Evaluating 8³e when e = 2
Now, let's substitute the value e = 2 into the expression:
8³e = 8³ * 2
Step 1: Calculate 8³
8³ means 8 multiplied by itself three times: 8 * 8 * 8 = 512
Step 2: Perform the Multiplication
Now, substitute the result from Step 1 into the expression:
512 * 2 = 1024
Therefore, the value of 8³e when e = 2 is 1024.
Expanding on the Concepts
Let's explore some related mathematical concepts to further solidify our understanding:
1. Exponents and Powers
Exponents (or indices) represent repeated multiplication. For example:
- x² = x * x
- x³ = x * x * x
- xⁿ = x multiplied by itself 'n' times
Understanding exponents is fundamental to algebra and many other branches of mathematics.
2. Variables and Constants
- Variables: These are symbols (usually letters like x, y, e, etc.) that represent unknown or changing values.
- Constants: These are fixed numerical values, like 8 in our example.
3. Algebraic Expressions
Algebraic expressions combine constants, variables, and mathematical operations (addition, subtraction, multiplication, division, exponents, etc.). They are essential for representing relationships between quantities and solving problems.
4. Evaluating Algebraic Expressions
Evaluating an algebraic expression means substituting specific values for the variables and then performing the calculations to find the numerical result. This is a crucial skill in algebra and its applications.
5. Importance of the Order of Operations
Following the correct order of operations is paramount. Incorrectly applying the order can lead to significantly different and incorrect results. Consider this example:
If we incorrectly calculated 8³ * 2 as (8 * 2)³ instead of 8³ * 2, we would get a completely different result:
(8 * 2)³ = 16³ = 4096
This highlights the importance of adhering strictly to PEMDAS/BODMAS.
Practical Applications
Evaluating algebraic expressions like 8³e is not just an academic exercise; it has numerous real-world applications:
- Physics: Calculating forces, velocities, or energies often involves substituting values into algebraic expressions.
- Engineering: Design and construction processes rely on algebraic expressions to model structures and systems.
- Finance: Calculating compound interest, loan payments, or investment returns often requires evaluating complex algebraic expressions.
- Computer Science: Programming frequently involves writing algorithms that evaluate mathematical expressions.
- Data Analysis: Statistical calculations, data manipulation, and analysis depend on evaluating numerous algebraic expressions.
Beyond Simple Substitution: More Complex Scenarios
While our example was straightforward, let's consider scenarios where the expression is more complex:
Scenario 1: Multiple Variables
Suppose we have the expression: 2a²b + 5c, where a = 3, b = 4, and c = 2. We would follow PEMDAS/BODMAS and substitute the values:
2(3)²(4) + 5(2) = 2(9)(4) + 10 = 72 + 10 = 82
Scenario 2: Parentheses/Brackets
Expressions with parentheses/brackets require us to evaluate the contents within the parentheses first. For example:
(5e + 2)³ when e = 2
(5(2) + 2)³ = (10 + 2)³ = 12³ = 1728
Scenario 3: Fractional Expressions
Fractional expressions also require careful attention to the order of operations. For example:
(8³ + e) / (2e - 1) when e = 2
(8³ + 2) / (2(2) - 1) = (512 + 2) / (4 - 1) = 514 / 3 ≈ 171.33
These examples demonstrate that while the fundamental concept of substituting values remains the same, the complexity of the expression increases the need for careful attention to detail and a thorough understanding of the order of operations.
Conclusion
Evaluating algebraic expressions, such as 8³e when e = 2, is a fundamental skill in mathematics with widespread applications. Understanding the order of operations (PEMDAS/BODMAS) is crucial for obtaining correct results. By breaking down the expression into smaller, manageable steps, and meticulously following the order of operations, we can accurately evaluate even complex algebraic expressions and apply these skills to numerous real-world problems. Remember to always practice and review these concepts to build a solid foundation in algebra and its practical applications. Consistent practice is key to mastering these skills and gaining confidence in tackling increasingly complex mathematical challenges.
Latest Posts
Latest Posts
-
Controls Overgrazing And Overproduction Of Public Lands
Jun 07, 2025
-
Which Of The Following Statements About Contributory Negligence Is True
Jun 07, 2025
-
A Warning Arc Can Be Displayed
Jun 07, 2025
-
The Blank Is A Symbol Of Rare And Special Things
Jun 07, 2025
-
Check All That Are True Statements Regarding Astrocytes
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Evaluate 8 3e When E 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.