Every Rhombus With Four Right Angles Is A Square.
Breaking News Today
Mar 27, 2025 · 5 min read
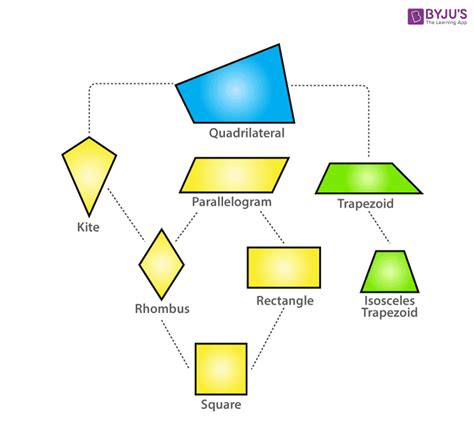
Table of Contents
Every Rhombus with Four Right Angles is a Square: A Deep Dive into Geometry
This article will rigorously prove the statement: "Every rhombus with four right angles is a square." We'll explore the definitions of rhombuses and squares, delve into the properties that define each shape, and ultimately demonstrate why the presence of four right angles in a rhombus necessitates it being a square. This exploration will not only solidify geometric understanding but also highlight the interconnectedness of geometric concepts. We'll also touch upon the practical applications of these concepts and explore some related mathematical ideas.
Understanding the Definitions: Rhombus and Square
Before embarking on the proof, let's ensure we have a clear understanding of the defining characteristics of a rhombus and a square.
What is a Rhombus?
A rhombus is a quadrilateral (a four-sided polygon) with all four sides having equal length. This is its defining property. Other properties, such as having opposite sides parallel, opposite angles equal, and diagonals bisecting each other at right angles, are consequences of this equal-side definition. Importantly, a rhombus doesn't necessarily have right angles.
What is a Square?
A square is a quadrilateral with four equal sides and four right angles. It is a special case of several other quadrilaterals, including a rectangle (a quadrilateral with four right angles) and a rhombus (a quadrilateral with four equal sides). The presence of both equal sides and right angles is crucial to defining a square.
Proof: Every Rhombus with Four Right Angles is a Square
The core of our argument rests on the definitions and properties we've outlined above. Let's assume we have a rhombus, which we'll call ABCD, with four right angles.
1. Starting with the Rhombus:
We begin with the premise that ABCD is a rhombus. By definition, this means:
- AB = BC = CD = DA (All four sides are equal in length)
2. Introducing the Right Angles:
Our additional premise is that all four angles are right angles:
- ∠A = ∠B = ∠C = ∠D = 90°
3. Utilizing Properties of Quadrilaterals:
A quadrilateral with four right angles is, by definition, a rectangle. Rectangles have opposite sides equal and parallel. Since our shape ABCD is already established as a rhombus (with all sides equal), the condition of having four right angles automatically transforms it into a rectangle.
4. The Intersection of Rhombus and Rectangle:
We now have a shape that is both a rhombus (all sides equal) and a rectangle (four right angles). The only quadrilateral that simultaneously satisfies both these conditions is a square.
5. Conclusion:
Therefore, since ABCD satisfies the conditions of both a rhombus and a rectangle, it must be a square. This proves our initial statement: Every rhombus with four right angles is a square.
Visualizing the Proof
Imagine constructing a rhombus. You start with four sticks of equal length. You can arrange these sticks to form various rhombuses – some will be skewed, having no right angles. However, if you constrain the angles to all be 90°, you're forced into creating a square. The equal sides are the defining characteristic of the rhombus, and the right angles force the shape into the specific form of a square. This visual representation aids intuitive understanding of the proof.
Expanding on Related Concepts
This proof highlights the interconnectedness of geometric concepts. Let's explore some related ideas:
Other Quadrilaterals
- Rectangle: A parallelogram with four right angles.
- Parallelogram: A quadrilateral with opposite sides parallel.
- Trapezoid (or Trapezium): A quadrilateral with at least one pair of parallel sides.
- Kite: A quadrilateral with two pairs of adjacent sides equal.
The relationships between these quadrilaterals illustrate a hierarchy within geometry. Squares are special cases of rectangles, which are special cases of parallelograms. The proof presented demonstrates how specific properties, when combined, lead to more restrictive and specific geometric shapes.
Coordinate Geometry Approach
The proof can also be approached using coordinate geometry. Let's place a rhombus on a Cartesian coordinate system. By defining the coordinates of the vertices and utilizing the distance formula and the slope formula, we can prove the equal side lengths and the right angles, ultimately leading to the conclusion that it's a square. This approach provides a different, analytical perspective on the same geometric truth.
Applications in Real Life
Understanding the properties of rhombuses and squares is not just a theoretical exercise. These shapes have numerous practical applications:
- Construction and Engineering: Squares and rhombuses are fundamental in structural design, ensuring stability and efficiency. From building foundations to bridge designs, the strength and stability inherent in these shapes are crucial.
- Art and Design: The symmetry and balance of these shapes make them aesthetically pleasing and frequently used in art, architecture, and graphic design.
- Tessellations: Squares, due to their ability to tile perfectly, are fundamental in creating regular tessellations, patterns used in various fields, from art to flooring.
Further Exploration: Beyond the Basics
The exploration doesn't end with this proof. We can consider more advanced topics:
- Higher Dimensions: The concepts of rhombuses and squares can be extended into higher dimensions, leading to more complex geometric objects with analogous properties.
- Non-Euclidean Geometry: Investigating these shapes in non-Euclidean geometries reveals fascinating differences and challenges our intuitive understanding.
- Transformations: Applying geometric transformations (like rotations, reflections, and translations) to a square or rhombus reveals their invariance under certain transformations, a significant concept in geometry.
Conclusion: A Foundation of Geometric Understanding
The proof that every rhombus with four right angles is a square is a cornerstone of geometric understanding. It demonstrates the power of precise definitions and logical deduction in establishing geometric truths. It also highlights the interconnectedness of different geometric concepts and provides a foundation for exploring more advanced topics. By understanding this fundamental principle, we gain a deeper appreciation for the elegance and practicality of geometry. This understanding extends beyond abstract mathematics, finding application in diverse real-world scenarios, emphasizing the value of geometric knowledge across multiple disciplines.
Latest Posts
Latest Posts
-
Carmen And Maria Are Studious In Spanish
May 09, 2025
-
The Overall Function Of The Calvin Cycle Is
May 09, 2025
-
Resting Your Foot On The Brake Pedal Is Called
May 09, 2025
-
A Disinfectant Is Used On Your Work Surface
May 09, 2025
-
The Kub Examination Looks For Defects In The
May 09, 2025
Related Post
Thank you for visiting our website which covers about Every Rhombus With Four Right Angles Is A Square. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.