Factor -1/2 Out Of -1/2x + 6
Breaking News Today
Jun 05, 2025 · 5 min read
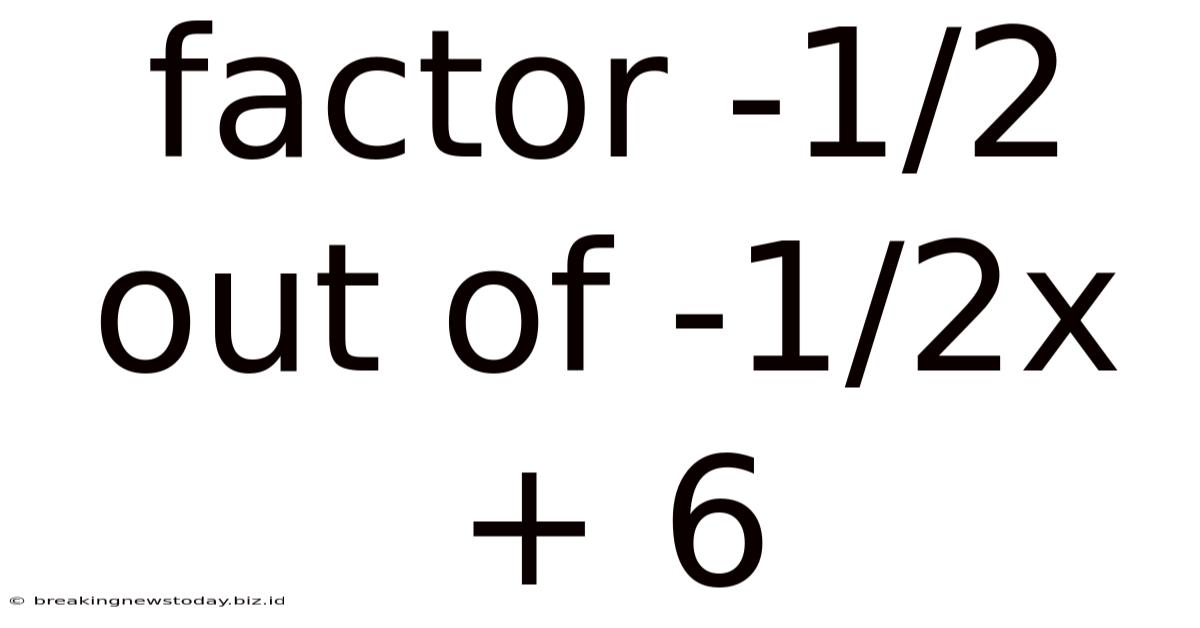
Table of Contents
Factoring Out -1/2: A Comprehensive Guide
Factoring is a fundamental algebraic operation with wide-ranging applications in mathematics and beyond. This article delves deep into the seemingly simple process of factoring out -1/2 from the expression -1/2x + 6, exploring the underlying principles, showcasing various approaches, and extending the concept to more complex scenarios. We'll also discuss the importance of factoring in solving equations, simplifying expressions, and its relevance in higher-level mathematics.
Understanding Factoring
Before tackling the specific problem, let's establish a solid understanding of what factoring entails. In essence, factoring is the process of rewriting an expression as a product of its factors. Think of it like reverse multiplication. If you multiply 3 by 4 to get 12, factoring 12 would give you 3 and 4 (or other factor pairs like 2 and 6, or 1 and 12).
In algebra, we often factor expressions involving variables. For example, factoring 2x + 4 would yield 2(x + 2). Here, 2 is a common factor of both terms, 2x and 4. We extract this common factor, leaving the remaining terms within parentheses.
Factoring -1/2 from -1/2x + 6: A Step-by-Step Approach
Our task is to factor out -1/2 from the expression -1/2x + 6. This involves identifying -1/2 as a common factor (or a common divisor) in both terms and then rewriting the expression as a product.
Step 1: Identify the Common Factor
Both -1/2x and 6 contain the factor -1/2. This might not be immediately obvious for the term 6, but let's consider how we can express 6 as a multiple of -1/2:
6 = -1/2 * (-12)
Now we can clearly see that -1/2 is a common factor.
Step 2: Rewrite the Expression
Now, rewrite the expression -1/2x + 6 using the common factor -1/2:
-1/2x + 6 = -1/2(x) + -1/2(-12)
Step 3: Factor Out the Common Factor
Since -1/2 is common to both terms, we can factor it out, leaving the remaining terms within parentheses:
-1/2(x) + -1/2(-12) = -1/2(x - 12)
Therefore, factoring -1/2 out of -1/2x + 6 gives us -1/2(x - 12).
Verification: Expanding the Factored Expression
To verify our result, we can expand the factored expression back to its original form. This involves distributing the -1/2 back into the parentheses:
-1/2(x - 12) = (-1/2)(x) + (-1/2)(-12) = -1/2x + 6
This confirms that our factoring is correct. The expanded form matches the original expression.
Alternative Approaches and Considerations
While the above method is straightforward, there are alternative approaches to factoring out fractions. Let’s consider a few:
1. Using Fraction Division:
We can also approach this problem by dividing each term by -1/2. Remember that dividing by a fraction is the same as multiplying by its reciprocal:
- -1/2x divided by -1/2: (-1/2x) / (-1/2) = (-1/2x) * (-2/1) = x
- 6 divided by -1/2: 6 / (-1/2) = 6 * (-2/1) = -12
Therefore, the factored form is -1/2(x - 12).
2. Working with Decimals:
Converting the fractions to decimals can sometimes simplify the process for those more comfortable with decimal arithmetic. -1/2 is equivalent to -0.5. The expression then becomes:
-0.5x + 6
To factor out -0.5, we divide each term by -0.5:
- -0.5x divided by -0.5: -0.5x / -0.5 = x
- 6 divided by -0.5: 6 / -0.5 = -12
Again, we arrive at the factored form -0.5(x - 12) which is equivalent to -1/2(x - 12).
3. Factoring out the Greatest Common Factor (GCF):
The concept extends to more complex scenarios involving multiple variables and terms. The most efficient approach is always to identify the greatest common factor (GCF) first. While -1/2 is a common factor in our example, it might not always be the greatest. In such cases, factor out the GCF to achieve the simplest factored form.
Applications of Factoring in Mathematics and Beyond
Factoring is a crucial tool in various mathematical contexts, including:
-
Solving Equations: Factoring quadratic equations (equations of the form ax² + bx + c = 0) is essential for finding their roots (solutions). Factoring allows us to rewrite the equation as a product of factors, making it easier to solve.
-
Simplifying Expressions: Factoring can simplify complex algebraic expressions, making them easier to manipulate and understand. This is particularly useful when dealing with fractions or rational expressions.
-
Calculus: Factoring plays a vital role in calculus, particularly in differentiation and integration. Simplifying expressions through factoring can streamline calculations and improve efficiency.
-
Real-world Applications: Factoring principles are applied in various fields, including physics, engineering, economics, and computer science, to model and solve real-world problems involving variables and relationships between quantities. For instance, it’s used to analyze projectile motion, design circuits, and model economic growth.
Advanced Factoring Techniques
While our example focused on a simple binomial expression, factoring techniques can be extended to more complex polynomials. These techniques include:
-
Factoring by Grouping: This technique is used when dealing with polynomials with four or more terms. It involves grouping terms with common factors and then factoring out the common factor from each group.
-
Factoring Trinomials: Factoring trinomials (polynomials with three terms) often involves finding two binomials whose product equals the trinomial. This typically involves reverse-FOIL (First, Outer, Inner, Last) techniques.
-
Difference of Squares: This technique is useful when factoring expressions of the form a² - b². The factored form is (a + b)(a - b).
-
Sum and Difference of Cubes: Similar to the difference of squares, there are specific formulas for factoring expressions involving the sum or difference of cubes.
Conclusion
Factoring out -1/2 from -1/2x + 6, resulting in -1/2(x - 12), is a basic yet illustrative example of a fundamental algebraic operation. Understanding this process lays the foundation for tackling more advanced factoring problems. The ability to proficiently factor expressions is paramount for success in algebra and its many applications in higher-level mathematics and real-world problem-solving. The diverse approaches presented in this article demonstrate the flexibility and adaptability of factoring techniques, ensuring a solid grasp of this essential mathematical concept. Remember that consistent practice and exploration of different methods will significantly improve your factoring skills.
Latest Posts
Latest Posts
-
Tearing A Magazine Page Is An Example Of
Jun 07, 2025
-
Which Statement Describes A Property Of Covalent Compounds
Jun 07, 2025
-
Drivers Should Be Courteous And Allow At Least
Jun 07, 2025
-
Complete These Sentences About Medieval Plays
Jun 07, 2025
-
What Holds The Dampening Coil Springs In Place
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Factor -1/2 Out Of -1/2x + 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.