Factor 15x3-5x2+6x-2 By Grouping. What Is The Resulting Expression
Breaking News Today
Jun 06, 2025 · 4 min read
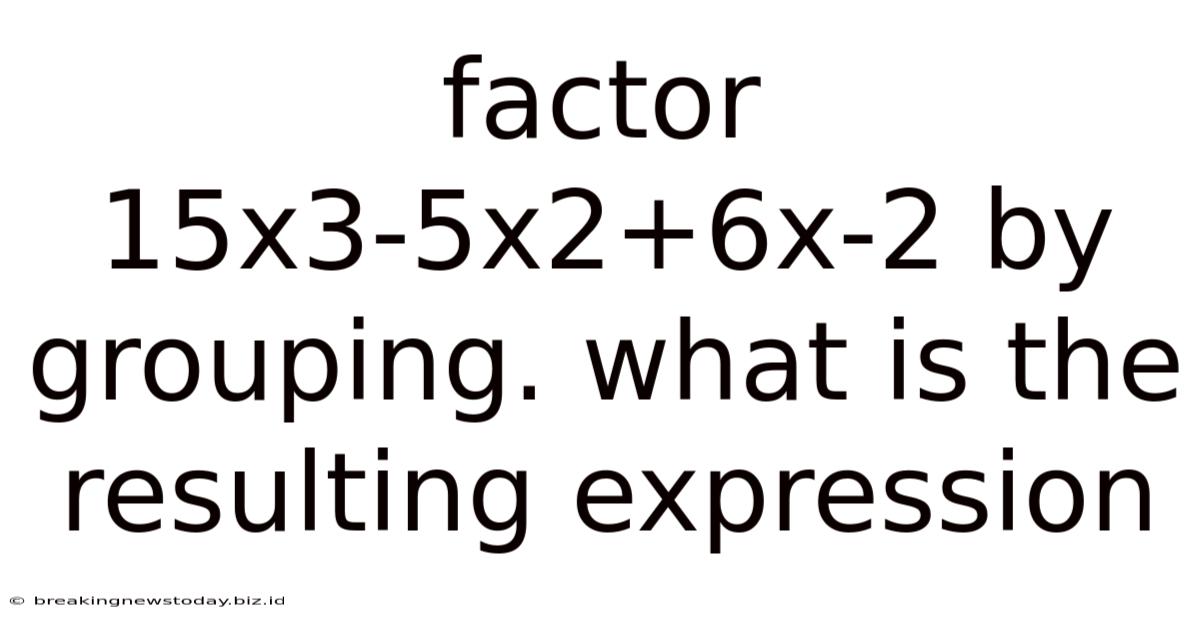
Table of Contents
Factoring 15x³ - 5x² + 6x - 2 by Grouping: A Comprehensive Guide
Factoring polynomials is a fundamental skill in algebra, crucial for solving equations, simplifying expressions, and understanding mathematical relationships. This article delves into the process of factoring the cubic polynomial 15x³ - 5x² + 6x - 2 using the grouping method. We'll explore the steps involved, potential pitfalls, and alternative approaches, providing a comprehensive understanding of this important algebraic technique.
Understanding Factoring by Grouping
Factoring by grouping is a technique used to factor polynomials with four or more terms. The method involves grouping terms with common factors, factoring out the greatest common factor (GCF) from each group, and then factoring out a common binomial factor. This process essentially reverses the distributive property of multiplication.
The Core Principle: The success of factoring by grouping hinges on strategically grouping terms to reveal a common binomial factor. This isn't always immediately obvious, and sometimes trial and error is necessary.
Step-by-Step Factoring of 15x³ - 5x² + 6x - 2
Let's apply the grouping method to factor 15x³ - 5x² + 6x - 2:
Step 1: Group the terms strategically.
We group the polynomial into two pairs of terms:
(15x³ - 5x²) + (6x - 2)
Step 2: Factor out the GCF from each group.
In the first group (15x³ - 5x²), the GCF is 5x². Factoring this out, we get:
5x²(3x - 1)
In the second group (6x - 2), the GCF is 2. Factoring this out, we get:
2(3x - 1)
Step 3: Identify the common binomial factor.
Notice that both terms now share a common binomial factor: (3x - 1).
Step 4: Factor out the common binomial factor.
We can factor out (3x - 1) from both terms:
(3x - 1)(5x² + 2)
Therefore, the factored form of 15x³ - 5x² + 6x - 2 is (3x - 1)(5x² + 2).
Verifying the Result
To verify our factoring is correct, we can expand the factored expression using the distributive property (also known as FOIL - First, Outer, Inner, Last):
(3x - 1)(5x² + 2) = 3x(5x²) + 3x(2) - 1(5x²) - 1(2) = 15x³ + 6x - 5x² - 2
Rearranging the terms, we get:
15x³ - 5x² + 6x - 2
This matches our original polynomial, confirming that our factoring is accurate.
Alternative Approaches and Considerations
While grouping worked effectively in this case, it's essential to understand that factoring polynomials can sometimes require alternative methods or a combination of techniques.
Trial and Error
For cubic polynomials, especially those with integer coefficients, a trial-and-error approach can sometimes be useful. This involves systematically testing different binomial factors until you find a combination that yields the original polynomial when expanded. This approach is often less efficient than grouping for higher-order polynomials.
Synthetic Division
Synthetic division is a more advanced technique that can be used to factor polynomials. It involves systematically testing potential roots of the polynomial to determine if they are factors. If a root is found, it corresponds to a linear factor. While effective, synthetic division involves a deeper understanding of polynomial roots.
The Rational Root Theorem
The rational root theorem provides a method for identifying potential rational roots of a polynomial with integer coefficients. This can be helpful in guiding the process of finding factors, but it doesn't guarantee a solution and may not be as straightforward as grouping for simpler polynomials.
Importance of Factoring Polynomials
The ability to factor polynomials is a cornerstone of algebraic manipulation and problem-solving. It has numerous applications in various fields including:
-
Solving Polynomial Equations: Factoring allows us to rewrite polynomial equations in a simpler form, making it easier to find their roots (solutions). This has applications in physics, engineering, and economics, where solutions to polynomial equations often represent significant physical quantities or parameters.
-
Simplifying Expressions: Factoring can significantly simplify complex algebraic expressions, making them easier to analyze and manipulate. This is crucial in calculus, where simplifying expressions often precedes differentiation or integration.
-
Calculus Applications: Factoring plays a vital role in calculus, particularly in finding limits, derivatives, and integrals. Being able to factor expressions can often dramatically simplify the process of these operations.
-
Graphing Polynomials: The factored form of a polynomial reveals its roots (x-intercepts) and often provides insights into its overall behavior and graph.
-
Curve Fitting: In data analysis, factoring polynomials helps with curve fitting, representing data points with polynomial models.
Conclusion: Mastering Factoring Techniques
Factoring the polynomial 15x³ - 5x² + 6x - 2 by grouping provided a clear illustration of this valuable algebraic technique. Remember that mastering polynomial factoring requires practice and understanding the underlying principles. While the grouping method is efficient for many cases, remember that other methods like trial and error, synthetic division, or the rational root theorem may be more suitable depending on the complexity of the polynomial and your available tools. A robust understanding of multiple factoring techniques equips you with the necessary skills for effectively tackling various algebraic challenges. Continued practice will hone your ability to recognize patterns and efficiently choose the most appropriate factoring method for a given problem. This, in turn, will strengthen your foundation in algebra and its applications in more advanced mathematical concepts.
Latest Posts
Latest Posts
-
Put The Sequence Of Events From Gilgamesh In Chronological
Jun 06, 2025
-
Suppose The Market For Apples Is Perfectly Competitive
Jun 06, 2025
-
Which Of The Following Is A Disadvantage Of Integrative Bargaining
Jun 06, 2025
-
What Is 52 437 Rounded To The Nearest Thousand
Jun 06, 2025
-
A Huge Flock Of Birds Right Above Us
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Factor 15x3-5x2+6x-2 By Grouping. What Is The Resulting Expression . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.