Factor 9z + 18 Using The Gcf
Breaking News Today
Jun 01, 2025 · 5 min read
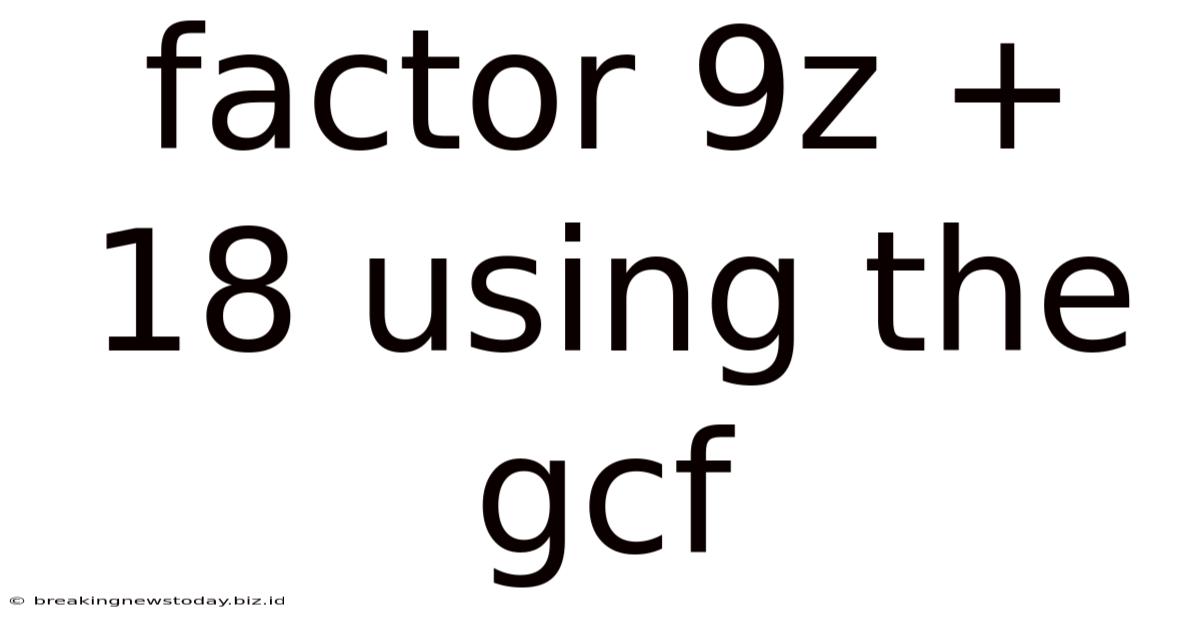
Table of Contents
Factoring 9z + 18 Using the GCF: A Comprehensive Guide
Factoring algebraic expressions is a fundamental skill in algebra, crucial for simplifying expressions, solving equations, and understanding more advanced mathematical concepts. This article will delve into the process of factoring the expression 9z + 18 using the greatest common factor (GCF), providing a thorough explanation suitable for beginners and a valuable refresher for those already familiar with the concept. We'll explore the steps involved, discuss the underlying principles, and offer examples to solidify your understanding.
Understanding the Greatest Common Factor (GCF)
Before diving into factoring 9z + 18, let's solidify our understanding of the GCF. The greatest common factor of two or more numbers or terms is the largest number or term that divides evenly into all of them. Finding the GCF is the cornerstone of many factoring techniques.
Finding the GCF of Numbers
Consider the numbers 12 and 18. To find their GCF, we can list the factors of each number:
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
The common factors are 1, 2, 3, and 6. The greatest of these is 6, therefore, the GCF of 12 and 18 is 6.
Alternatively, we can use prime factorization. Prime factorization breaks a number down into its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
- Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
The common prime factors are 2 and 3. The lowest power of 2 is 2¹ and the lowest power of 3 is 3¹. Multiplying these gives us 2 x 3 = 6, confirming the GCF is 6.
Finding the GCF of Variables
When dealing with variables, we look for the lowest power of each variable present in all terms. For example, consider the terms x², x³, and x⁵. The GCF is x², as it's the lowest power of x among the three terms.
Factoring 9z + 18 Using the GCF
Now, let's apply our understanding of GCF to factor the expression 9z + 18.
Step 1: Find the GCF of the coefficients.
The coefficients in the expression 9z + 18 are 9 and 18.
- Factors of 9: 1, 3, 9
- Factors of 18: 1, 2, 3, 6, 9, 18
The GCF of 9 and 18 is 9.
Step 2: Find the GCF of the variables.
The expression contains the variable 'z' only in the first term. Therefore, there's no common variable factor.
Step 3: Factor out the GCF.
Since the GCF of the coefficients is 9 and there's no common variable, we factor out 9 from both terms:
9z + 18 = 9(z) + 9(2)
Step 4: Rewrite the expression.
We can rewrite the expression by factoring out the GCF:
9z + 18 = 9(z + 2)
Therefore, the factored form of 9z + 18 is 9(z + 2).
Verifying the Factored Form
To verify our factoring, we can expand the factored form using the distributive property:
9(z + 2) = 9 * z + 9 * 2 = 9z + 18
This confirms that our factoring is correct.
Advanced Applications and Extensions
While this example focuses on a simple binomial expression, the principle of finding the GCF and factoring it out remains crucial for more complex expressions. Let's explore some extensions:
Factoring Trinomials
Consider the trinomial 6x² + 12x + 18. The GCF of the coefficients (6, 12, and 18) is 6. Factoring out the GCF gives:
6x² + 12x + 18 = 6(x² + 2x + 3)
In this case, the resulting expression (x² + 2x + 3) might require further factoring techniques, depending on whether it can be factored further.
Factoring Polynomials with Multiple Variables
The same principle applies to polynomials with multiple variables. For example, consider the polynomial 4xy + 8x²y² + 12x³y³
The GCF of the coefficients is 4. The lowest power of x is x¹ and the lowest power of y is y¹. Therefore, the GCF is 4xy.
Factoring out the GCF gives:
4xy + 8x²y² + 12x³y³ = 4xy(1 + 2xy + 3x²y²)
Practical Applications in Problem Solving
Factoring using the GCF is not just an abstract algebraic manipulation. It has significant practical applications in various fields:
- Simplification of algebraic expressions: Factoring simplifies expressions, making them easier to work with in further calculations.
- Solving equations: Factoring is a key technique for solving quadratic and higher-degree equations. The zero product property states that if the product of factors is zero, then at least one of the factors must be zero.
- Calculus: Factoring is essential in calculus for simplifying derivatives and integrals.
- Physics and Engineering: Many physical laws and engineering principles are expressed using algebraic equations that often require factoring for analysis and problem-solving.
Troubleshooting Common Mistakes
While factoring using the GCF is a relatively straightforward process, some common mistakes can occur:
- Incorrectly identifying the GCF: Double-check your work to ensure you have found the greatest common factor of both the coefficients and the variables.
- Incompletely factoring: Ensure that you have factored out the GCF from all terms in the expression.
- Arithmetic errors: Carefully check your calculations to avoid errors in finding the GCF and factoring the expression.
Conclusion: Mastering GCF Factoring
Mastering the skill of factoring using the greatest common factor is crucial for success in algebra and related fields. By understanding the principles behind finding the GCF, carefully following the steps outlined above, and practicing regularly, you will develop confidence and proficiency in this essential algebraic technique. Remember to always verify your factored form by expanding it to ensure it matches the original expression. This comprehensive guide provides a solid foundation for tackling more complex factoring problems in the future. Continue practicing and exploring different types of factoring problems to hone your skills and deepen your understanding of this fundamental algebraic concept.
Latest Posts
Latest Posts
-
Executing In The Ipde Process Primarily Involves
Jun 02, 2025
-
Identify The Type Of Irony In The Scenario Below
Jun 02, 2025
-
Stacking And Piling Is Another Term For What Structural System
Jun 02, 2025
-
What Do Locksmiths Usually Do Idle Guy
Jun 02, 2025
-
Which Action Most Makes Creon A Villain In This Story
Jun 02, 2025
Related Post
Thank you for visiting our website which covers about Factor 9z + 18 Using The Gcf . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.