Factor In Simplest Form 6x 12
Breaking News Today
Jun 06, 2025 · 5 min read
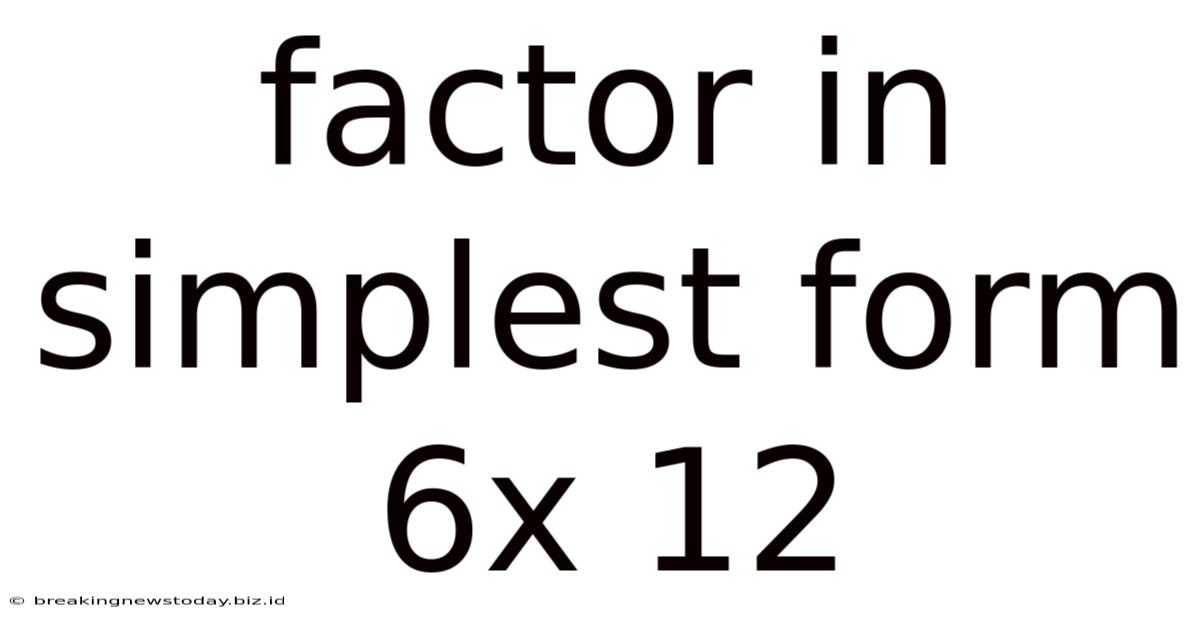
Table of Contents
Factoring 6x + 12: A Comprehensive Guide
Understanding how to factor algebraic expressions is a fundamental skill in algebra. This seemingly simple expression, 6x + 12, provides an excellent opportunity to explore various factoring techniques and delve into the underlying mathematical concepts. This article will guide you through the process of factoring 6x + 12 into its simplest form, explaining each step and exploring related concepts. We'll also look at why factoring is important and how it applies to more complex algebraic problems.
What is Factoring?
Factoring, in the context of algebra, is the process of breaking down a mathematical expression into smaller, simpler expressions that when multiplied together, give you the original expression. Think of it like reverse multiplication. For instance, if you multiply 2 and 3, you get 6. Factoring 6 would be finding those two numbers (2 and 3) that, when multiplied, result in 6.
In the case of algebraic expressions like 6x + 12, we're looking for expressions that, when multiplied, yield the original expression. This process is crucial for simplifying expressions, solving equations, and understanding the underlying structure of mathematical relationships.
Greatest Common Factor (GCF)
The most common and often the first method used in factoring is finding the Greatest Common Factor (GCF). The GCF is the largest number or expression that divides evenly into all terms of the expression. To find the GCF of 6x + 12, we look at the numerical coefficients (6 and 12) and the variable terms (x and no x).
-
Numerical Coefficients: The factors of 6 are 1, 2, 3, and 6. The factors of 12 are 1, 2, 3, 4, 6, and 12. The greatest common factor between 6 and 12 is 6.
-
Variable Terms: The term 6x contains the variable 'x', while the term 12 does not. Therefore, there is no common variable factor.
Therefore, the GCF of 6x + 12 is 6.
Factoring 6x + 12 Using the GCF
Now that we've identified the GCF, we can factor it out of the expression 6x + 12. This involves dividing each term of the expression by the GCF and writing the result in parentheses, with the GCF outside the parentheses.
6x + 12 = 6(x + 2)
Let's verify this:
If we distribute the 6 back into the parentheses, we get:
6 * x + 6 * 2 = 6x + 12
This confirms that our factoring is correct. The simplest form of 6x + 12 is 6(x + 2).
Why is Factoring Important?
Factoring is not just a procedural step; it's a fundamental concept with numerous applications in algebra and beyond. Here are some key reasons why factoring is essential:
-
Simplifying Expressions: Factoring simplifies complex expressions, making them easier to understand and work with. This is crucial when solving equations or performing other algebraic manipulations.
-
Solving Equations: Many algebraic equations can only be solved efficiently by factoring. For instance, quadratic equations (equations of the form ax² + bx + c = 0) are often solved by factoring.
-
Finding Roots and Zeros: Factoring allows us to find the roots (or zeros) of a polynomial equation. The roots are the values of the variable that make the equation equal to zero. These roots represent important points on the graph of the polynomial.
-
Analyzing Graphs: The factored form of a polynomial provides valuable information about its graph, including its x-intercepts, vertex, and overall shape.
-
Real-World Applications: Factoring has applications in various fields, including physics, engineering, economics, and computer science, where it's used to model and solve real-world problems.
Extending the Concept: Factoring More Complex Expressions
While 6x + 12 is a relatively simple expression, the principles of factoring apply to more complex polynomials. Let's briefly explore some examples:
1. Factoring Trinomials: Trinomials are expressions with three terms, such as x² + 5x + 6. Factoring trinomials often involves finding two binomials (expressions with two terms) that, when multiplied, result in the original trinomial. This often involves techniques like the "ac method" or trial and error. For x² + 5x + 6, the factored form is (x + 2)(x + 3).
2. Factoring by Grouping: This technique is used for polynomials with four or more terms. It involves grouping terms with common factors and then factoring out the common factor from each group. For example, the expression 2xy + 2xz + 3y + 3z can be factored by grouping as 2x(y + z) + 3(y + z) = (2x + 3)(y + z).
3. Factoring the Difference of Squares: Expressions of the form a² - b² can be factored as (a + b)(a - b). This is a special case of factoring that's useful in various algebraic manipulations.
4. Factoring Perfect Square Trinomials: Expressions of the form a² + 2ab + b² or a² - 2ab + b² can be factored as (a + b)² or (a - b)², respectively. These are also special cases with easily recognizable patterns.
Practical Applications and Examples
Let's look at some real-world scenarios where understanding factoring is beneficial:
-
Calculating Area: Imagine you have a rectangular garden with a length of (x + 2) meters and a width of 6 meters. The area of the garden is given by the expression 6(x + 2) square meters. Factoring helps express the area in a simplified and understandable way.
-
Projectile Motion: In physics, the trajectory of a projectile can be modeled using quadratic equations. Factoring these equations can help determine the time it takes for the projectile to reach the ground or its maximum height.
-
Financial Modeling: Compound interest calculations often involve polynomial expressions. Factoring these expressions can simplify the process of determining investment growth over time.
-
Optimization Problems: In engineering and other fields, optimization problems often involve finding the maximum or minimum value of a function. Factoring can help simplify the expression and make finding the optimal solution easier.
Conclusion: Mastering Factoring
Factoring algebraic expressions is a fundamental skill in algebra and beyond. The seemingly simple task of factoring 6x + 12 into 6(x + 2) provides a solid foundation for understanding more complex factoring techniques. By mastering factoring, you'll not only simplify algebraic expressions but also gain a deeper understanding of mathematical relationships and their application in various real-world scenarios. Continue practicing different types of factoring problems, and you'll quickly develop proficiency in this essential algebraic skill. Remember to always check your work by expanding the factored form to ensure it matches the original expression. This consistent practice will solidify your understanding and build confidence in your ability to tackle more challenging algebraic problems.
Latest Posts
Latest Posts
-
Which Statement Explains What Geologists Can Learn From The Graph
Jun 07, 2025
-
Which Sentence Best Contrasts Two Things
Jun 07, 2025
-
18 Is 24 Of What Number
Jun 07, 2025
-
Some Polyhedrons Are Both Prisms And Pyramids
Jun 07, 2025
-
Which Shows A Successful Communication Strategy For An Adolescent
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Factor In Simplest Form 6x 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.