Factor The Expression Completely Over The Complex Numbers.x3+5x2+9x+45
Breaking News Today
Jun 04, 2025 · 5 min read
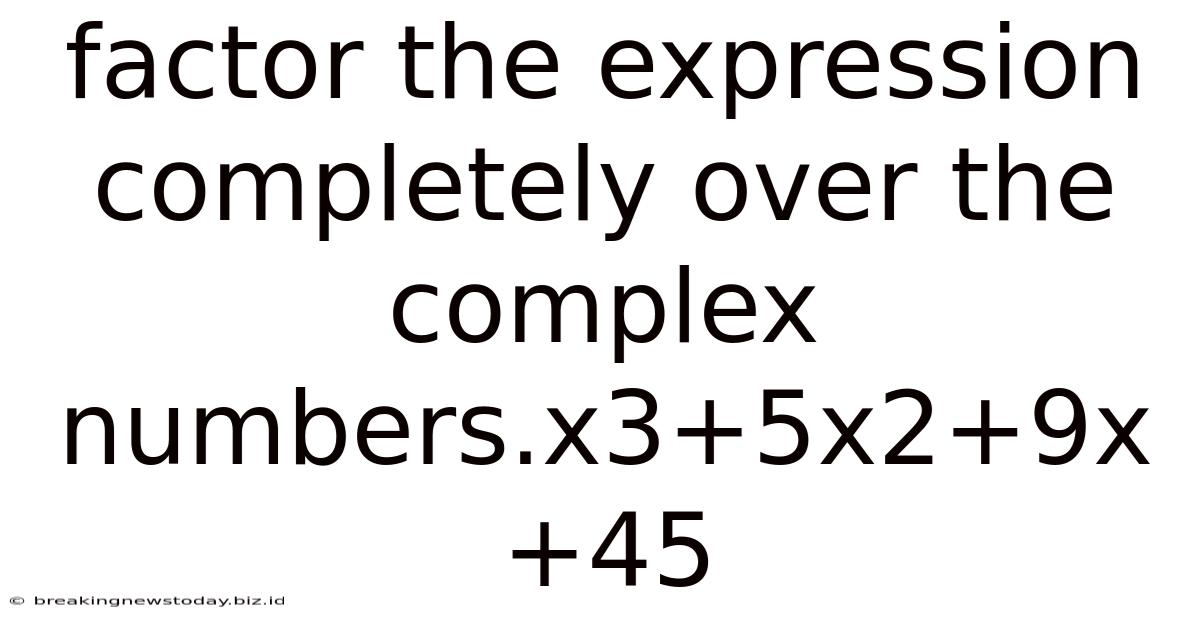
Table of Contents
Factoring the Expression Completely Over the Complex Numbers: x³ + 5x² + 9x + 45
Factoring polynomials is a fundamental concept in algebra with wide-ranging applications in various fields, from calculus and engineering to computer science and cryptography. While factoring over the real numbers presents its challenges, factoring over the complex numbers opens up a world of possibilities, enabling the complete factorization of any polynomial. This article will delve into the process of factoring the cubic polynomial x³ + 5x² + 9x + 45 completely over the complex numbers. We'll explore various techniques, including the Rational Root Theorem, polynomial long division, and the quadratic formula, culminating in a complete and insightful understanding of the solution.
Understanding the Problem: Factoring over Complex Numbers
The expression x³ + 5x² + 9x + 45 is a cubic polynomial. This means it has three roots (or zeros), which are the values of x that make the expression equal to zero. When factoring over the real numbers, we might only find some, or even none, of these roots. However, the Fundamental Theorem of Algebra guarantees that a polynomial of degree n has exactly n roots in the complex numbers (including real numbers, which are a subset of complex numbers). These roots might be real or complex (involving the imaginary unit i, where i² = -1). Our goal is to find all three roots and express the polynomial as a product of three linear factors.
Applying the Rational Root Theorem
The Rational Root Theorem provides a systematic way to identify potential rational roots (roots that are rational numbers, i.e., fractions of integers). It states that if a polynomial has a rational root p/q (where p and q are integers and q ≠ 0), then p is a factor of the constant term (45 in this case) and q is a factor of the leading coefficient (1 in this case).
The factors of 45 are ±1, ±3, ±5, ±9, ±15, ±45. The factors of 1 are ±1. Therefore, the potential rational roots are ±1, ±3, ±5, ±9, ±15, ±45.
Let's test these potential roots by substituting them into the polynomial:
- f(1) = 1 + 5 + 9 + 45 = 60 ≠ 0
- f(-1) = -1 + 5 - 9 + 45 = 40 ≠ 0
- f(3) = 27 + 45 + 27 + 45 = 144 ≠ 0
- f(-3) = -27 + 45 - 27 + 45 = 36 ≠ 0
- f(5) = 125 + 125 + 45 + 45 = 340 ≠ 0
- f(-5) = -125 + 125 - 45 + 45 = 0
We found a root! x = -5 is a root of the polynomial. This means (x + 5) is a factor.
Polynomial Long Division
Now that we have one factor (x + 5), we can use polynomial long division to find the other factor. Dividing x³ + 5x² + 9x + 45 by (x + 5), we get:
x² + 9
x + 5 | x³ + 5x² + 9x + 45
- (x³ + 5x²)
----------------
9x + 45
- (9x + 45)
----------------
0
The quotient is x² + 9. Therefore, we can rewrite the polynomial as:
(x + 5)(x² + 9)
Factoring the Quadratic: x² + 9
Now we need to factor the quadratic expression x² + 9. This quadratic has no real roots because its discriminant (b² - 4ac) is negative: 0² - 4(1)(9) = -36. However, we can factor it using complex numbers.
We can rewrite x² + 9 as x² - (3i)² where i is the imaginary unit (i² = -1). This is a difference of squares, which factors as:
(x - 3i)(x + 3i)
Complete Factorization
Combining the factors, we have the complete factorization of x³ + 5x² + 9x + 45 over the complex numbers:
(x + 5)(x - 3i)(x + 3i)
This represents the polynomial as a product of three linear factors, each corresponding to one of its roots: -5, 3i, and -3i.
Further Exploration: Implications and Applications
The ability to factor polynomials completely over the complex numbers has profound implications across various mathematical fields and practical applications:
- Finding all roots: The Fundamental Theorem of Algebra, underpinning this process, guarantees that we can find all roots of any polynomial, no matter how high its degree. This has significant implications for solving equations and analyzing mathematical models.
- Solving differential equations: In calculus, solving differential equations often involves finding the roots of characteristic polynomials. The ability to factor these polynomials over the complex numbers allows for the complete solution of these differential equations.
- Signal processing and control systems: In engineering, control systems and signal processing rely heavily on the analysis of polynomials and their roots. Complex roots represent oscillations and dampening in systems, which are crucial for designing stable and efficient systems.
- Quantum mechanics: Complex numbers play a fundamental role in quantum mechanics, where wave functions and their associated equations involve complex roots and factorizations.
- Cryptography: The properties of polynomials and their factorizations are leveraged in various cryptographic algorithms to ensure data security.
Conclusion: A Powerful Tool in Mathematics
Factoring the expression x³ + 5x² + 9x + 45 completely over the complex numbers demonstrates the power and elegance of complex numbers in algebra. The techniques used—the Rational Root Theorem, polynomial long division, and factoring over complex numbers—represent fundamental tools for solving a wide variety of mathematical problems with far-reaching applications in science, engineering, and technology. By understanding these methods, we gain a deeper appreciation for the richness and complexity of polynomial algebra and its pervasive influence on various scientific disciplines. The complete factorization (x + 5)(x - 3i)(x + 3i) provides not just a solution but a deeper understanding of the underlying structure of the polynomial. This understanding is crucial for tackling more complex polynomial problems and for appreciating the significance of complex numbers in mathematics and its applications.
Latest Posts
Latest Posts
-
Introduction To Vocabulary Labeling Sorting And Ranking Questions
Jun 06, 2025
-
800 Is 1 10 Of What Number
Jun 06, 2025
-
What Makes The Oak Tree Special For Janya
Jun 06, 2025
-
Which Statements Accurately Compare Beowulf And Grendel
Jun 06, 2025
-
What Else Is Produced During The Combustion Of Propane C3h8
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Factor The Expression Completely Over The Complex Numbers.x3+5x2+9x+45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.