Factor The Expression Over The Complex Numbers. X2+18
Breaking News Today
Jun 02, 2025 · 5 min read
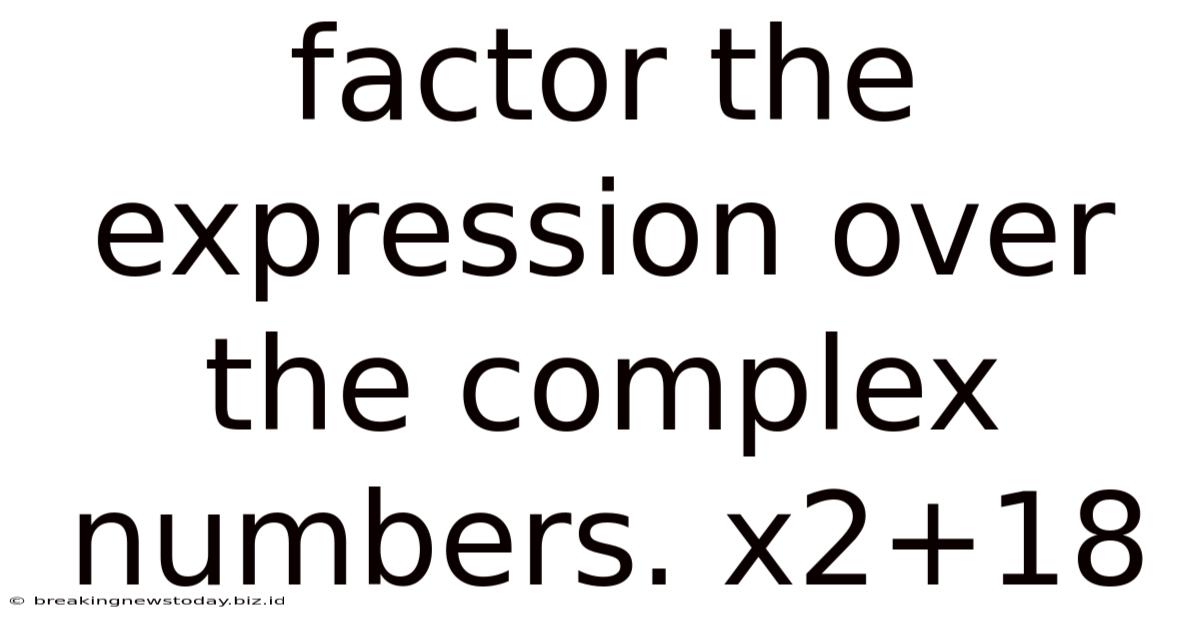
Table of Contents
Factoring the Expression x² + 18 Over the Complex Numbers
Factoring expressions is a fundamental concept in algebra, crucial for solving equations, simplifying expressions, and understanding the behavior of functions. While factoring over the real numbers often presents straightforward solutions, venturing into the realm of complex numbers opens up new possibilities and allows for the complete factorization of expressions that are irreducible over the reals. This article will delve into the process of factoring the expression x² + 18 over the complex numbers, explaining the steps involved and exploring the broader implications of working within the complex number system.
Understanding Complex Numbers
Before diving into the factorization, let's refresh our understanding of complex numbers. Complex numbers are numbers of the form a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit, defined as the square root of -1 (i² = -1). The real part of the complex number is 'a', and the imaginary part is 'b'.
The introduction of the imaginary unit 'i' allows us to solve equations that have no solutions in the real number system. For instance, the equation x² = -1 has no real solutions, but it has two complex solutions: x = i and x = -i. This is because i² = -1 and (-i)² = -1.
Factoring x² + 18 Over the Real Numbers
Initially, let's attempt to factor x² + 18 over the real numbers. We look for two real numbers that multiply to 18 and add to 0 (since there's no x term). However, no such real numbers exist. This is because 18 is a positive number, and the only way to obtain a positive product is by multiplying two positive numbers or two negative numbers. Neither pair will add up to zero. Therefore, x² + 18 is irreducible over the real numbers.
Factoring x² + 18 Over the Complex Numbers
The inability to factor x² + 18 over the real numbers doesn't mean it's unfactorable. The key lies in extending our number system to include complex numbers. We can rewrite the expression as:
x² + 18 = 0
Subtracting 18 from both sides, we get:
x² = -18
Now, we can take the square root of both sides:
x = ±√(-18)
Since √(-1) = i, we can rewrite the expression as:
x = ±√(18)√(-1) = ±√(18)i
We can simplify √18 further:
√18 = √(9 * 2) = 3√2
Therefore, the solutions are:
x = 3√2i and x = -3√2i
These are the roots of the quadratic equation x² + 18 = 0. Now, we can express the factorization using these roots:
x² + 18 = (x - 3√2i)(x + 3√2i)
This is the complete factorization of x² + 18 over the complex numbers. Notice that the factors are complex conjugates of each other. Complex conjugates are pairs of complex numbers that have the same real part but opposite imaginary parts. This is a common characteristic when factoring quadratic expressions over the complex numbers.
Verification
To verify our factorization, let's expand the expression:
(x - 3√2i)(x + 3√2i) = x² + 3√2ix - 3√2ix - (3√2i)²
Since (3√2i)² = 9 * 2 * i² = 18i² = -18, the expression simplifies to:
x² - (-18) = x² + 18
This confirms that our factorization is correct.
The Significance of Complex Factorization
The ability to factor expressions over the complex numbers has significant implications in various areas of mathematics and its applications:
1. Solving Polynomial Equations:
Complex numbers allow us to find all roots (solutions) of any polynomial equation, regardless of its degree. The Fundamental Theorem of Algebra states that a polynomial of degree n has exactly n complex roots (counting multiplicity). Without complex numbers, we would only be able to find some of the roots, leaving the others unresolved.
2. Signal Processing and Electrical Engineering:
Complex numbers are extensively used in signal processing and electrical engineering. They provide a powerful tool for analyzing and manipulating signals, such as those encountered in radio waves, audio signals, and electrical circuits. The concepts of impedance and admittance in AC circuits rely heavily on complex numbers.
3. Quantum Mechanics:
Complex numbers play a fundamental role in quantum mechanics, where they describe the wave functions of particles and the probabilities of quantum events. The use of complex numbers is essential for formulating and solving the Schrödinger equation, which governs the behavior of quantum systems.
4. Fractals and Chaos Theory:
Complex numbers are instrumental in generating fractals, like the Mandelbrot set and Julia sets. These beautiful and complex patterns arise from iterating simple functions involving complex numbers, revealing surprising and intricate structures. Complex numbers are also used in the study of chaotic systems, where seemingly simple systems can exhibit highly unpredictable behavior.
5. Advanced Mathematical Analysis:
Complex numbers provide a richer and more powerful framework for analyzing functions and solving differential equations. The use of complex analysis allows us to solve problems that are intractable using only real numbers.
Conclusion: Embracing the Power of Complex Numbers
Factoring the expression x² + 18 over the complex numbers demonstrates the power and elegance of extending our mathematical toolkit beyond the real numbers. The ability to find all roots of polynomial equations and the insights gained from working within the complex number system have profound implications across various fields of science and engineering. By embracing the world of complex numbers, we unlock a deeper understanding of mathematical structures and their applications in the real world. Mastering complex number factorization opens doors to more advanced mathematical concepts and allows for a more complete and comprehensive understanding of algebraic structures. The seemingly simple act of factoring x² + 18 over the complex numbers reveals a vast and fascinating landscape of mathematical possibilities.
Latest Posts
Latest Posts
-
Sarah Sights The Top Of The Statue Of Liberty
Jun 04, 2025
-
Which Describes Oxygen Content As Earth Evolved Over Time
Jun 04, 2025
-
A Student Drew The Following Flowchart
Jun 04, 2025
-
Serving Utensils Are Used When Serving Food In Order To
Jun 04, 2025
-
Air Cap Pressure Gauges Allow The Refinish Technician To
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about Factor The Expression Over The Complex Numbers. X2+18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.