Factor The Expression Over The Complex Numbers. X2+36
Breaking News Today
Jun 06, 2025 · 4 min read
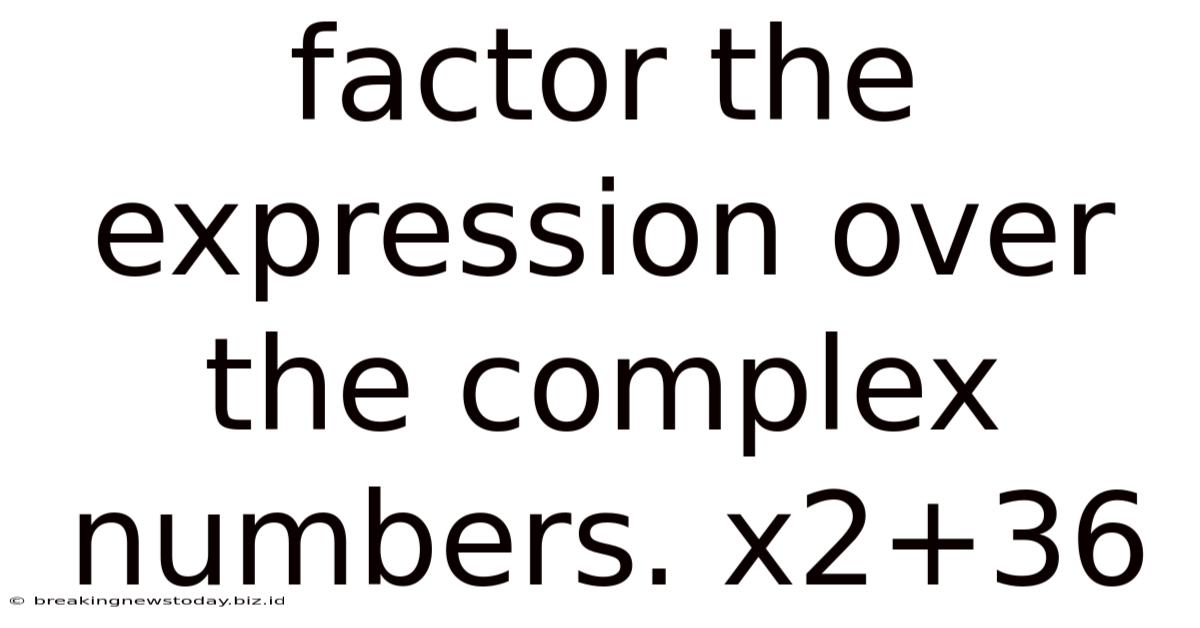
Table of Contents
Factoring the Expression x² + 36 Over the Complex Numbers
Factoring expressions is a fundamental concept in algebra, crucial for solving equations, simplifying expressions, and understanding the behavior of functions. While factoring over the real numbers often involves finding integer or rational roots, factoring over the complex numbers opens up a wider range of possibilities, allowing us to find solutions even when real number solutions don't exist. This article delves deep into factoring the expression x² + 36 over the complex numbers, exploring the underlying principles and demonstrating the process step-by-step. We'll also touch upon the significance of complex numbers in various mathematical fields.
Understanding the Problem: x² + 36
The expression x² + 36 is a quadratic expression, meaning it's a polynomial of degree two. When attempting to factor this over the real numbers, we'd look for two numbers that multiply to 36 and add to 0 (the coefficient of the x term). However, no such real numbers exist. This is where the power of complex numbers comes in.
What are Complex Numbers?
Complex numbers extend the real number system by introducing the imaginary unit, i, defined as the square root of -1 (√-1 = i). A complex number is expressed in the form a + bi, where 'a' and 'b' are real numbers, 'a' is the real part, and 'b' is the imaginary part.
The introduction of i allows us to find square roots of negative numbers, which are crucial in solving equations like x² + 36 = 0.
Factoring x² + 36 Using the Difference of Squares
While x² + 36 doesn't seem to fit the typical difference of squares formula (a² - b² = (a + b)(a - b)), we can cleverly manipulate it using the imaginary unit. Remember that i² = -1. We can rewrite the expression as:
x² - (-36)
Now we can treat -36 as (6i)², since (6i)² = 6² * i² = 36 * (-1) = -36. This transforms our expression into a difference of squares:
x² - (6i)²
Now we can apply the difference of squares formula:
x² - (6i)² = (x + 6i)(x - 6i)
Therefore, the factored form of x² + 36 over the complex numbers is (x + 6i)(x - 6i).
Verification: Expanding the Factored Form
To verify our factoring, we can expand the factored form using the FOIL method (First, Outer, Inner, Last):
(x + 6i)(x - 6i) = x² - 6ix + 6ix - (6i)²
The middle terms, -6ix and +6ix, cancel each other out, leaving:
x² - (6i)² = x² - (-36) = x² + 36
This confirms that our factoring is correct.
Solving the Quadratic Equation x² + 36 = 0
The factored form allows us to easily solve the quadratic equation x² + 36 = 0:
(x + 6i)(x - 6i) = 0
This equation is satisfied if either (x + 6i) = 0 or (x - 6i) = 0. Solving for x in each case gives us the solutions:
x = -6i and x = 6i
These are the complex roots of the quadratic equation.
Significance of Complex Numbers in Mathematics and Beyond
Complex numbers might seem abstract initially, but they play a vital role in numerous areas of mathematics and science:
1. Solving Polynomial Equations:
The Fundamental Theorem of Algebra states that a polynomial of degree n has exactly n complex roots (including multiplicities). This means that complex numbers are essential for finding all solutions to polynomial equations, even those that don't have real roots.
2. Electrical Engineering:
Complex numbers are fundamental in analyzing alternating current (AC) circuits. Impedance, a measure of opposition to current flow, is often represented as a complex number, simplifying calculations involving resistors, capacitors, and inductors.
3. Quantum Mechanics:
Complex numbers are integral to the mathematical framework of quantum mechanics. Wave functions, describing the state of a quantum system, are often complex-valued.
4. Signal Processing:
Complex numbers are used extensively in signal processing to represent and manipulate signals in the frequency domain. The Fourier transform, a crucial tool in signal processing, relies heavily on complex numbers.
5. Fractals and Chaos Theory:
Complex numbers are at the heart of generating many beautiful and intricate fractals, such as the Mandelbrot set. These fractals arise from iterative calculations involving complex numbers, revealing complex patterns and behaviors.
Further Exploration: Higher-Degree Polynomials and Complex Numbers
The principles discussed for factoring x² + 36 extend to higher-degree polynomials. While factoring higher-degree polynomials can be more challenging, the use of complex numbers ensures that we can always find all the roots, regardless of whether they are real or complex. Techniques like the quadratic formula and more advanced methods like numerical root-finding algorithms are used to find these roots.
Conclusion: The Power of Complex Numbers in Factoring
Factoring the expression x² + 36 over the complex numbers demonstrates the power and utility of extending the number system beyond real numbers. By introducing the imaginary unit i, we can solve equations that were previously unsolvable within the real number system, gaining valuable insights into various mathematical and scientific fields. The process of factoring, seemingly simple for some expressions, becomes a gateway to deeper understanding when exploring the rich world of complex numbers. Understanding complex numbers empowers us to tackle more complex mathematical problems and unlock deeper understanding in diverse disciplines. The ability to factor over the complex numbers is a critical skill in advanced mathematics and its applications.
Latest Posts
Latest Posts
-
At What Type Of Boundary Do Strike Strip Basins Form
Jun 06, 2025
-
What Is The Mean Of The Dataset 12 1 2
Jun 06, 2025
-
Four Basic Commands For A Good Breakdown Position
Jun 06, 2025
-
The Easiest Component Of Biodiversity To Measure Is
Jun 06, 2025
-
In The Tudor Court Artistic Focus Was On Religious Painting
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Factor The Expression Over The Complex Numbers. X2+36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.