Fifteen More Than Half A Number Is 9
Breaking News Today
Jun 07, 2025 · 5 min read
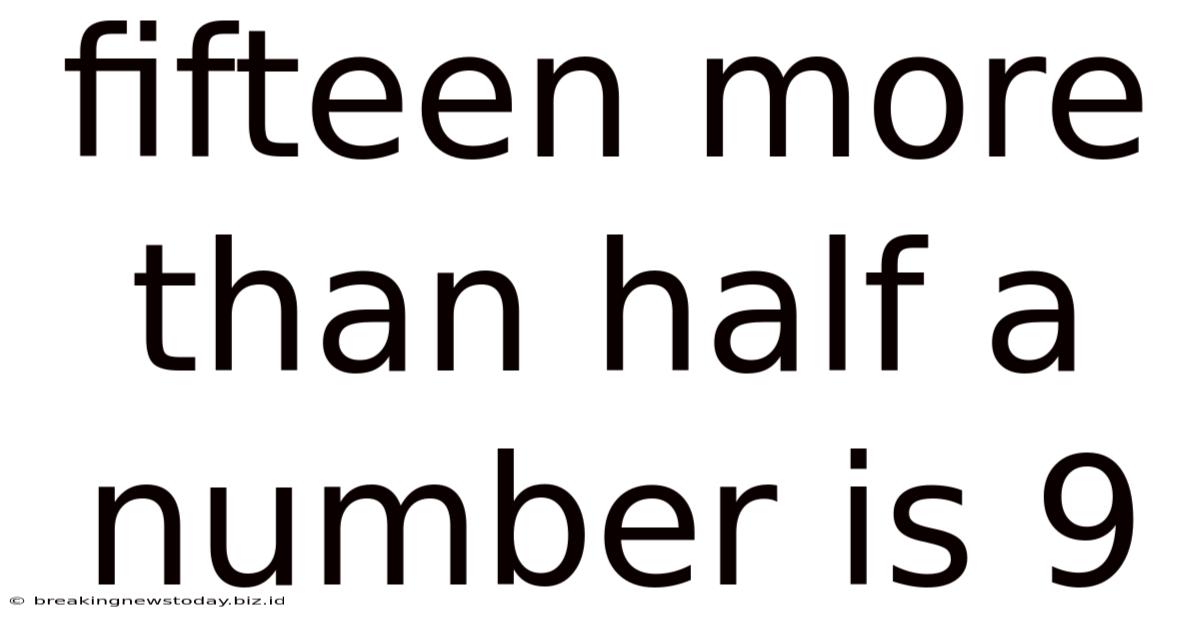
Table of Contents
Fifteen More Than Half a Number Is 9: A Deep Dive into Problem Solving
This seemingly simple mathematical statement, "Fifteen more than half a number is 9," opens a door to a world of problem-solving strategies and mathematical concepts. While the solution might seem immediately obvious to some, exploring the different approaches to solving this equation reveals fundamental principles applicable to far more complex mathematical challenges. This article will delve into various methods to solve this problem, explore the underlying mathematical concepts, and highlight the importance of understanding the underlying structure of word problems.
Understanding the Problem: Deconstructing the Sentence
Before diving into the solutions, let's meticulously break down the sentence: "Fifteen more than half a number is 9." Each part carries significant weight in formulating the correct equation:
-
"A number": This represents an unknown value, typically represented by a variable like x, y, or n. We'll use x for consistency.
-
"Half a number": This translates directly to x/2 or 0.5x.
-
"Fifteen more than half a number": This indicates we need to add 15 to the "half a number" expression, resulting in x/2 + 15.
-
"is 9": This signifies that the entire expression (x/2 + 15) equals 9.
Therefore, the complete equation representing the word problem is: x/2 + 15 = 9
Method 1: Solving the Equation Algebraically
This is the most straightforward approach, relying on basic algebraic manipulation:
-
Subtract 15 from both sides: This isolates the term containing the variable x. The equation becomes: x/2 = 9 - 15, which simplifies to x/2 = -6.
-
Multiply both sides by 2: This eliminates the fraction, leaving x alone. The equation becomes: x = -6 * 2, which simplifies to x = -12.
Therefore, the number is -12. Let's verify this: Half of -12 is -6, and fifteen more than -6 is indeed 9.
Method 2: Using a Visual Representation
While algebraic manipulation is efficient, visualizing the problem can be beneficial, especially for those who find abstract concepts challenging. We can represent this problem using a number line or even simple diagrams:
Imagine a number line. We know that "fifteen more than half a number" lands us at 9. To find the "half a number," we need to move 15 units to the left on the number line from 9. This brings us to -6. Since this represents half the number, doubling -6 gives us the final answer: -12.
This visual approach helps solidify the understanding of the problem's structure and the steps involved in finding the solution.
Method 3: Working Backwards
This method involves reversing the operations described in the problem statement. We start with the final result (9) and work backward:
-
"Fifteen more than...": This implies that 15 was added to obtain 9. Subtracting 15 from 9 gives us: 9 - 15 = -6.
-
"...half a number": This indicates that -6 represents half the number. Multiplying -6 by 2 gives us the full number: -6 * 2 = -12.
This approach showcases the inverse relationship between addition and subtraction, and multiplication and division.
Exploring Deeper Mathematical Concepts
Solving this seemingly simple equation touches upon several fundamental mathematical concepts:
-
Variables and Equations: The problem introduces the concept of a variable (x) representing an unknown quantity and how it can be manipulated within an equation.
-
Linear Equations: The equation x/2 + 15 = 9 is a simple linear equation, which means it represents a straight line when graphed. Solving linear equations is a fundamental skill in algebra.
-
Inverse Operations: The solution relies heavily on using inverse operations (subtraction to undo addition, division to undo multiplication) to isolate the variable.
-
Number Line Representation: Visualizing the problem on a number line reinforces the concept of negative numbers and their relationship to positive numbers.
Applying the Problem-Solving Strategy to More Complex Scenarios
The strategies used to solve "Fifteen more than half a number is 9" are transferable to much more complex mathematical problems. The key takeaways are:
-
Careful Deconstruction: Breaking down complex word problems into smaller, manageable parts is crucial. Identify keywords and phrases that translate directly into mathematical operations.
-
Systematic Approach: Develop a structured approach to problem-solving, whether it's algebraic manipulation, visual representation, or working backward. Consistency is key.
-
Verification: Always check your answer by substituting it back into the original equation to ensure it satisfies the conditions of the problem.
Expanding the Problem: Variations and Extensions
Let's explore variations of this problem to further solidify our understanding:
-
What if the problem stated: "Fifteen less than half a number is 9"? The equation would change to x/2 - 15 = 9, leading to a different solution.
-
What if the problem involved a different fraction or a different constant? For instance, "Twenty more than a third of a number is 10" would require similar problem-solving techniques but with different numerical values.
-
What if we introduced another unknown variable? For example, "Fifteen more than half a number, plus another number, is 9." This would introduce a system of equations, requiring more advanced algebraic techniques to solve.
These variations highlight the adaptability of the problem-solving strategies discussed earlier. They underscore the importance of understanding the underlying mathematical principles rather than simply memorizing a single solution method.
The Importance of Word Problems in Mathematics Education
Word problems are not merely exercises; they are essential for developing critical thinking and problem-solving skills. They bridge the gap between abstract mathematical concepts and real-world applications. The ability to translate a real-world scenario into a mathematical equation is a crucial skill in various fields, from engineering and finance to computer science and data analysis. The seemingly simple problem, "Fifteen more than half a number is 9," serves as a microcosm of this crucial skill-building process.
Conclusion: Beyond the Answer
While the solution to "Fifteen more than half a number is 9" is -12, the true value lies in the process of arriving at that solution. The problem provides a valuable opportunity to practice and reinforce fundamental algebraic concepts, develop problem-solving strategies, and appreciate the power of translating real-world scenarios into mathematical models. This simple equation acts as a gateway to a broader understanding of mathematics and its applications in various aspects of life. By understanding the underlying principles, you are not just solving a problem; you're building a foundation for tackling more complex challenges in the future.
Latest Posts
Latest Posts
-
Cougars Which Can Live In Many Climates Are Skilled Hunters
Jun 07, 2025
-
As A Percentage 22 00 Is Equal To Of 40 00
Jun 07, 2025
-
Which Equation Is Correct Regarding The Measure Of 1
Jun 07, 2025
-
Classify Each Description As A Parameter Or A Statistic
Jun 07, 2025
-
Which Indicator Shows The An Prc 152 Multiband Radio
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Fifteen More Than Half A Number Is 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.