Find Half Of Seven And Three Fourths
Breaking News Today
Jun 01, 2025 · 5 min read
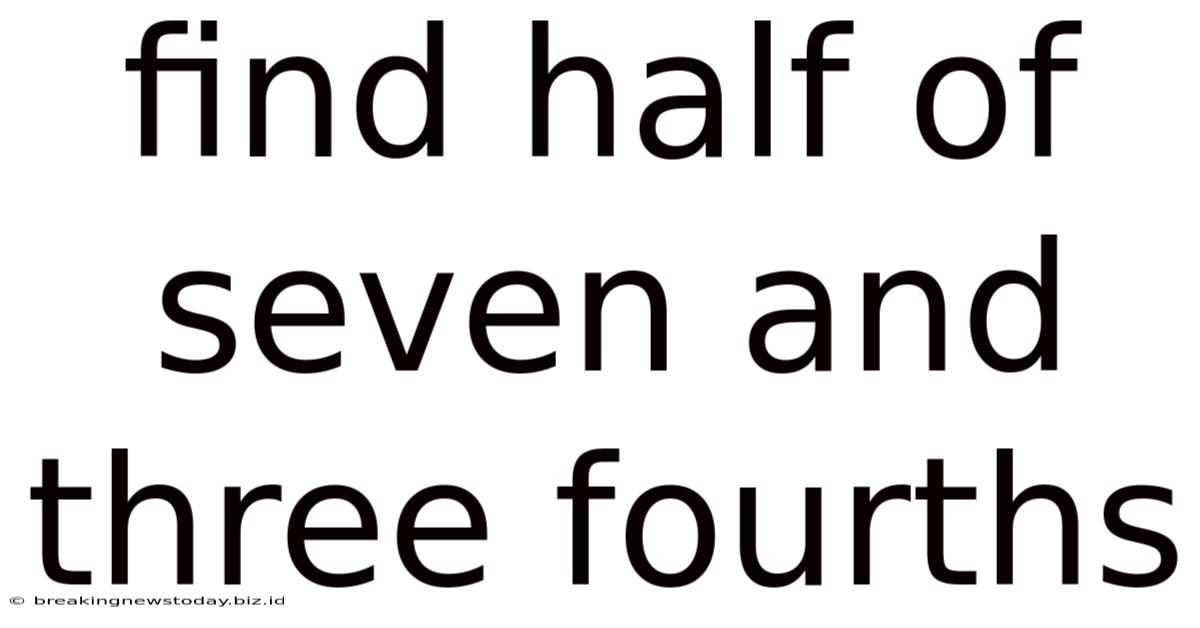
Table of Contents
Finding Half of Seven and Three Fourths: A Comprehensive Guide
Finding half of any number is a fundamental mathematical operation, crucial for various applications from everyday calculations to advanced mathematical problems. This article delves into the process of finding half of seven and three-fourths (7 ¾), exploring different methods and demonstrating their practical application. We’ll cover various approaches, catering to different skill levels and learning styles, ensuring a thorough understanding of the concept.
Understanding Fractions and Mixed Numbers
Before we embark on finding half of 7 ¾, it’s essential to grasp the basics of fractions and mixed numbers. A fraction represents a part of a whole, expressed as a numerator (top number) over a denominator (bottom number). For instance, ¾ represents three parts out of four equal parts. A mixed number, like 7 ¾, combines a whole number (7) with a fraction (¾).
Converting Mixed Numbers to Improper Fractions
To simplify calculations involving mixed numbers, it’s often beneficial to convert them into improper fractions. An improper fraction has a numerator larger than or equal to its denominator. To convert 7 ¾ to an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 7 * 4 = 28
- Add the numerator to the result: 28 + 3 = 31
- Keep the same denominator: The denominator remains 4.
Therefore, 7 ¾ is equivalent to the improper fraction 31/4.
Method 1: Finding Half by Dividing by Two
The most straightforward method to find half of any number is to divide it by two. We can apply this directly to the improper fraction:
(1/2) * (31/4)
To multiply fractions, we multiply the numerators together and the denominators together:
(1 * 31) / (2 * 4) = 31/8
This improper fraction can be converted back into a mixed number:
31 divided by 8 is 3 with a remainder of 7. Therefore, 31/8 equals 3 ⅞.
Method 2: Finding Half by Dividing the Whole and Fractional Parts Separately
Another approach involves finding half of the whole number part and the fractional part separately and then combining the results.
-
Find half of the whole number: Half of 7 is 7/2 = 3.5
-
Find half of the fractional part: Half of ¾ is (1/2) * (3/4) = 3/8
-
Combine the results: 3.5 + 3/8 = 3 ½ + 3/8
To add these, we need a common denominator. We can convert 3 ½ to an improper fraction: (3 * 2 + 1)/2 = 7/2. Then we find a common denominator for 7/2 and 3/8, which is 8.
(7/2) * (4/4) = 28/8 28/8 + 3/8 = 31/8
Converting this back to a mixed number gives us 3 ⅞.
Method 3: Using Decimal Representation
This method involves converting the mixed number to a decimal and then dividing by two.
-
Convert the fraction to a decimal: ¾ = 0.75
-
Convert the mixed number to a decimal: 7 ¾ = 7 + 0.75 = 7.75
-
Divide by two: 7.75 / 2 = 3.875
This decimal can be converted back to a fraction:
- The whole number is 3.
- The decimal part, 0.875, can be expressed as 875/1000. Simplifying this fraction by dividing both numerator and denominator by 125, we get 7/8.
Therefore, 3.875 is equal to 3 ⅞.
Comparing the Methods
All three methods yield the same result: 3 ⅞. The choice of method depends on personal preference and the context of the problem. The first method (dividing the improper fraction by two) is generally the most concise and efficient, particularly for those comfortable working with fractions. The second method (dividing whole and fractional parts separately) can be more intuitive for some learners, while the third method (using decimal representation) might be preferred when dealing with calculations that require decimal precision.
Real-World Applications
Understanding how to find half of a mixed number has numerous real-world applications:
-
Cooking and Baking: Many recipes require halving or doubling ingredients. If a recipe calls for 7 ¾ cups of flour, knowing how to find half is crucial for adjusting the recipe.
-
Construction and Engineering: Precise measurements are essential in construction and engineering. Calculations involving fractions and mixed numbers are commonplace, and finding half of a measurement is a frequent requirement.
-
Finance and Budgeting: Dividing expenses or incomes often involves fractions and mixed numbers. For instance, splitting a bill equally amongst friends might require calculating half of a total amount expressed as a mixed number.
-
Sewing and Crafting: Pattern adjustments in sewing and other crafts frequently involve calculations with fractions and mixed numbers.
-
Data Analysis: In data analysis, averaging or scaling data can involve working with fractional values and necessitates an understanding of operations with fractions and mixed numbers.
Expanding the Concept: Finding Other Fractions of Seven and Three Fourths
The techniques discussed above can be extended to finding other fractions of 7 ¾. For example, to find one-third of 7 ¾:
-
Convert 7 ¾ to an improper fraction: 31/4
-
Multiply by one-third: (1/3) * (31/4) = 31/12
-
Convert to a mixed number: 31/12 = 2 7/12
Similarly, you can adapt these methods to find any fraction of 7 ¾. The key is to convert the mixed number to an improper fraction for easier calculation, and then simplify the result.
Conclusion
Finding half of seven and three-fourths, or any fraction of a mixed number, is a fundamental skill with broad applications. By understanding the different methods – dividing the improper fraction by two, dividing the whole and fractional parts separately, and using decimal representation – you can effectively tackle these types of problems. The ability to confidently perform these calculations is invaluable across various fields, from culinary arts to engineering and beyond. Mastering these techniques will strengthen your mathematical abilities and enhance your problem-solving skills in numerous everyday situations.
Latest Posts
Latest Posts
-
How Do Nearby Businesses With Similar Products Usually Compete
Jun 02, 2025
-
Why Didnt Beneatha Want To Be A Doctor Anymore
Jun 02, 2025
-
4 1 Additional Practice Inverse Variation And The Reciprocal Function
Jun 02, 2025
-
24 65 Rounded To The Nearest Tenth
Jun 02, 2025
-
Your Field Of Vision Is Greatly Reduced By
Jun 02, 2025
Related Post
Thank you for visiting our website which covers about Find Half Of Seven And Three Fourths . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.