Find The Fourth Proportional To The Number 5 7 30
Breaking News Today
Jun 02, 2025 · 6 min read
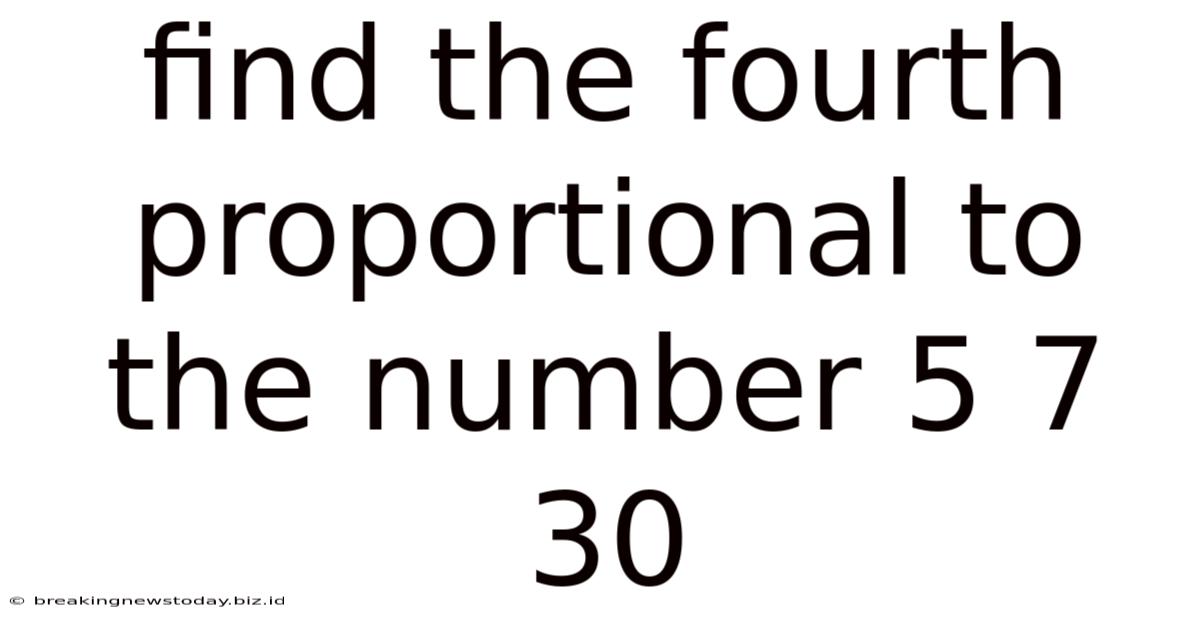
Table of Contents
Finding the Fourth Proportional: A Deep Dive into Ratios and Proportions
Finding the fourth proportional to the numbers 5, 7, and 30 might seem like a simple mathematical problem at first glance. However, understanding the underlying concepts of ratios and proportions, and mastering the techniques to solve such problems, opens doors to a wide range of applications in various fields, from basic arithmetic to advanced engineering and scientific calculations. This comprehensive guide will delve into the intricacies of this seemingly simple problem, providing a thorough understanding of the principles involved and exploring various methods for finding the solution. We will also examine the practical applications of this concept in diverse contexts.
Understanding Ratios and Proportions
Before we tackle the problem of finding the fourth proportional to 5, 7, and 30, let's solidify our understanding of the fundamental concepts of ratios and proportions.
What is a Ratio?
A ratio is a comparison of two or more quantities. It shows the relative sizes of the quantities. For example, the ratio of apples to oranges in a fruit basket containing 3 apples and 5 oranges is 3:5. Ratios can be expressed in various forms:
- Colon notation: 3:5
- Fraction notation: 3/5
- Using the word "to": 3 to 5
What is a Proportion?
A proportion is a statement that two ratios are equal. It signifies that the relationship between the quantities in one ratio is the same as the relationship between the quantities in the other ratio. For instance, the proportion 3:5 = 6:10 indicates that the ratio of 3 to 5 is equivalent to the ratio of 6 to 10.
Types of Proportions:
-
Direct Proportion: In a direct proportion, as one quantity increases, the other quantity increases proportionally. For example, if you buy more apples (increase in quantity), you pay more money (increase in cost).
-
Inverse Proportion: In an inverse proportion, as one quantity increases, the other quantity decreases proportionally. For example, if you increase the speed of your travel, the time taken to reach your destination decreases.
Finding the Fourth Proportional
The problem at hand is to find the fourth proportional to the numbers 5, 7, and 30. This means we need to find a number 'x' such that the ratio 5:7 is equal to the ratio 30:x. This can be expressed as a proportion:
5/7 = 30/x
There are several ways to solve for 'x':
Method 1: Cross-Multiplication
This is perhaps the most straightforward method. We cross-multiply the terms in the proportion:
5 * x = 7 * 30
5x = 210
x = 210/5
x = 42
Therefore, the fourth proportional to 5, 7, and 30 is 42.
Method 2: Using the concept of scaling
We can also approach this problem by considering the scaling factor between the first and third numbers. We see that 30 is 6 times larger than 5 (30/5 = 6). To maintain the proportion, we need to scale the second number (7) by the same factor:
7 * 6 = 42
Again, we find that the fourth proportional is 42.
Verifying the Solution
Let's verify our solution by substituting x = 42 back into the original proportion:
5/7 = 30/42
Simplifying both ratios by dividing by their greatest common divisor:
5/7 = (30 ÷ 6) / (42 ÷ 6) = 5/7
Since both ratios are equal, our solution is correct. The fourth proportional to 5, 7, and 30 is indeed 42.
Real-World Applications of Proportions
The concept of finding the fourth proportional, and more broadly, working with ratios and proportions, has widespread applications in various real-world scenarios. Here are a few examples:
1. Scaling Recipes: When cooking, you often need to adjust recipes to serve more or fewer people. This involves using proportions to scale the ingredient quantities appropriately. For example, if a recipe calls for 2 cups of flour and 1 cup of sugar, and you want to double the recipe, you simply multiply both quantities by 2 (resulting in 4 cups of flour and 2 cups of sugar).
2. Map Scales: Maps use scales to represent distances on the ground. For instance, a map scale of 1:100,000 means that 1 centimeter on the map represents 100,000 centimeters (or 1 kilometer) on the ground. Finding distances on the map using this scale involves working with proportions.
3. Engineering and Construction: Engineers and construction professionals use ratios and proportions extensively in their calculations. This includes determining the strength of materials, calculating structural loads, and designing building plans to scale.
4. Financial Calculations: Proportions are used in many financial calculations, such as calculating interest rates, determining investment returns, and analyzing financial ratios of companies.
5. Scientific Experiments: In scientific research, proportions are crucial for controlling variables in experiments and ensuring accurate measurements. For example, in chemistry, mixing solutions with precise ratios is often critical to obtaining the desired results.
6. Medical Dosage: Doctors and nurses use proportions to calculate appropriate medication dosages based on a patient's weight or body surface area. Precise calculations are vital in ensuring patient safety and efficacy of treatment.
Expanding the Concept: Continued Proportion
While our problem focused on finding a single fourth proportional, the concept extends to continued proportions. A continued proportion is a series of ratios where the ratio of consecutive terms is constant. For example, a, b, c, and d are in continued proportion if a/b = b/c = c/d.
Advanced Techniques and Problem Solving Strategies
While cross-multiplication and scaling provide simple solutions for basic problems, more complex scenarios may require more sophisticated techniques. These include:
- Using logarithms: For proportions involving very large or very small numbers, logarithms can simplify calculations.
- Matrices and linear algebra: For systems of proportions, matrix methods provide efficient solutions.
- Software tools: Spreadsheet software and mathematical software packages can be used to solve complex proportion problems quickly and accurately.
Conclusion: Mastering Ratios and Proportions for Success
The seemingly simple problem of finding the fourth proportional to 5, 7, and 30 serves as a gateway to understanding the broader world of ratios and proportions. Mastering these concepts is crucial not only for solving mathematical problems but also for navigating various real-world applications. The methods described in this article provide a solid foundation for tackling these types of problems with confidence, whether they involve simple cross-multiplication or more advanced techniques. By understanding the principles of ratios, proportions, and their various applications, you equip yourself with valuable problem-solving skills applicable across numerous disciplines. This knowledge empowers you to confidently tackle challenges, analyze data, and make informed decisions in a variety of professional and personal contexts. Continuous practice and exploration of more complex scenarios will further solidify your understanding and enhance your problem-solving capabilities in this essential area of mathematics.
Latest Posts
Latest Posts
-
Absorption Rate Factors Help An Employee Understand
Jun 04, 2025
-
Gina Wilson All Things Algebra Llc 2020
Jun 04, 2025
-
Over Which Interval Of The Domain Is Function M Negative
Jun 04, 2025
-
Which Of The Following Best Describes The Lochner Decision
Jun 04, 2025
-
Buying A New House Can Increase Ones Stress Level
Jun 04, 2025
Related Post
Thank you for visiting our website which covers about Find The Fourth Proportional To The Number 5 7 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.