Find The Geometric Mean Of 8 And 28.
Breaking News Today
Jun 04, 2025 · 6 min read
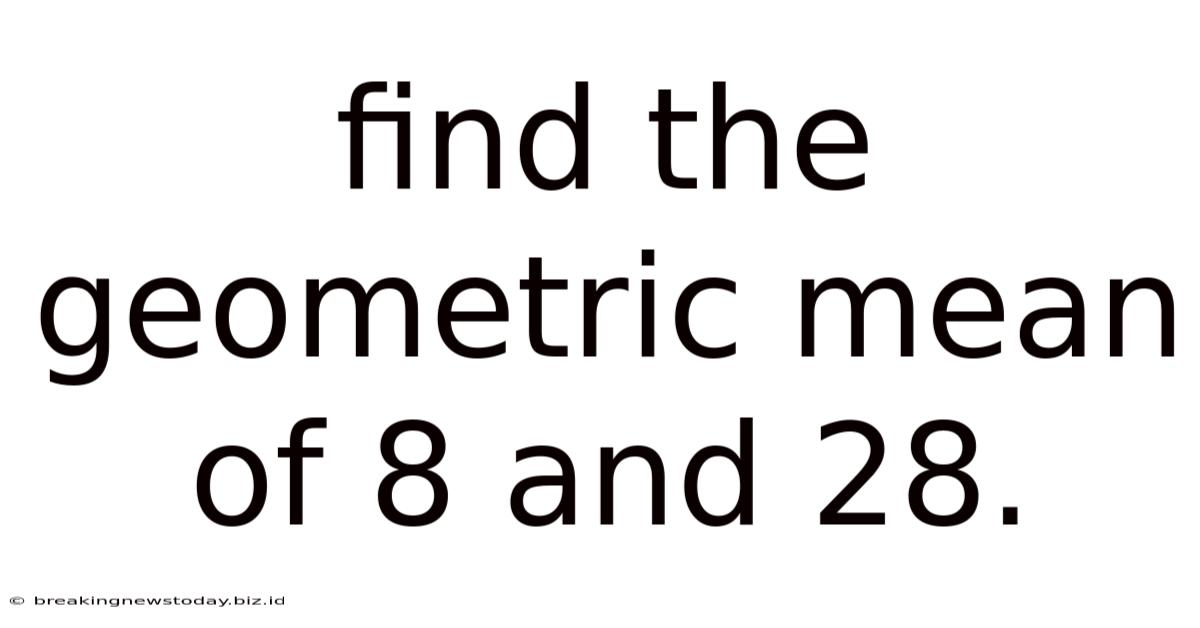
Table of Contents
Finding the Geometric Mean: A Comprehensive Guide with Example (8 and 28)
The geometric mean (GM) is a crucial concept in mathematics and statistics, offering a unique way to average numbers, particularly when dealing with multiplicative relationships or data expressed as percentages or ratios. Unlike the arithmetic mean, which simply adds numbers and divides by the count, the geometric mean multiplies numbers and then finds the nth root, where 'n' represents the total number of values. This article will provide a comprehensive understanding of the geometric mean, explain its calculation, explore its applications, and, of course, solve the problem of finding the geometric mean of 8 and 28.
Understanding the Geometric Mean
The geometric mean is a type of average that indicates the central tendency or typical value of a set of numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). It's particularly useful when dealing with:
- Rates of change: Calculating average growth rates over time.
- Financial analysis: Determining average returns on investments.
- Geometric figures: Calculating average side lengths or dimensions.
- Proportions: Finding the mean of ratios or proportions.
The formula for calculating the geometric mean is:
GM = ⁿ√(x₁ * x₂ * x₃ * ... * xₙ)
Where:
- GM represents the geometric mean.
- ⁿ√ denotes the nth root (where 'n' is the number of values).
- x₁, x₂, x₃, ..., xₙ represent the individual values in the dataset.
Calculating the Geometric Mean of 8 and 28
Let's apply this knowledge to find the geometric mean of 8 and 28. Following the formula:
GM = ²√(8 * 28)
-
Multiply the numbers: 8 * 28 = 224
-
Find the square root: ²√224 ≈ 14.97
Therefore, the geometric mean of 8 and 28 is approximately 14.97.
Applications of the Geometric Mean
The geometric mean's versatility makes it applicable across numerous fields. Here are some key examples:
1. Finance and Investment
The geometric mean is frequently used in finance to calculate the average annual growth rate of an investment over multiple periods. This is because it accounts for the compounding effect of returns. Simple arithmetic averaging can misrepresent the actual average growth, especially over volatile periods. The geometric mean provides a more accurate reflection of the overall investment performance.
For instance, if an investment grows by 10% in year one and 20% in year two, the arithmetic mean would be 15%, suggesting a constant 15% growth. However, the geometric mean would account for the compounding effect, providing a more accurate picture of the actual average growth.
2. Growth Rates and Indices
In various sectors, such as population growth, economic growth, and disease progression, the geometric mean is valuable for calculating average rates of change over time. It considers the multiplicative nature of these processes, providing a more robust measure than the arithmetic mean.
Imagine tracking the growth of a bacterial colony. If it doubles in size on day one and triples on day two, a simple average of the growth factors (2 and 3) would be 2.5. However, this doesn't accurately reflect the overall growth. The geometric mean would provide a more precise representation of the average daily growth rate.
3. Image Processing and Scaling
In image processing and computer graphics, the geometric mean is used in scaling operations and image resizing. Maintaining aspect ratios during scaling often requires the geometric mean to preserve proportions.
4. Data Normalization
When dealing with datasets where values span several orders of magnitude, the geometric mean can help normalize the data, making it easier to analyze and compare. This is particularly useful in fields like environmental science where measurements might range from very small to very large values.
5. Statistical Analysis
The geometric mean plays a role in advanced statistical techniques, including the calculation of certain descriptive statistics and the analysis of data with multiplicative relationships. It's crucial in fields like quality control and reliability engineering.
Geometric Mean vs. Arithmetic Mean: Key Differences
The geometric mean and the arithmetic mean differ significantly in their calculation and interpretation. Understanding these differences is crucial for choosing the appropriate average for a given situation.
| Feature | Geometric Mean | Arithmetic Mean |
|---|---|---|
| Calculation | Product of values, then nth root | Sum of values, divided by the number of values |
| Effect of outliers | Less sensitive to outliers | More sensitive to outliers |
| Applications | Rates of change, multiplicative relationships | Additive relationships, evenly distributed data |
| Interpretation | Represents average multiplicative factor | Represents average additive factor |
In essence, the arithmetic mean is suitable for situations where the data points contribute additively, whereas the geometric mean is better suited for situations where the data points contribute multiplicatively.
Limitations of the Geometric Mean
While the geometric mean offers numerous advantages, it's essential to acknowledge its limitations:
-
Zero or Negative Values: The geometric mean cannot be calculated if any of the values are zero or negative. This is because the product of values containing zeros will be zero, and the root of a negative number is not a real number. In such cases, alternative methods are necessary.
-
Interpretation: Interpreting the geometric mean might be less intuitive than the arithmetic mean, especially for those unfamiliar with its principles.
-
Data Distribution: The geometric mean is most appropriate for data that is positively skewed or follows a logarithmic distribution. It may not accurately represent the central tendency of other data distributions.
Advanced Concepts and Variations
Several extensions and variations build upon the basic geometric mean concept:
-
Weighted Geometric Mean: This assigns weights to each value based on its relative importance, modifying the contribution of each value to the overall mean.
-
Generalized Geometric Mean: This extends the concept to a broader range of mathematical functions.
-
Geometric Median: Unlike the geometric mean, which is calculated using the product of values, the geometric median minimizes the sum of distances between the data points and itself in a geometric sense.
Conclusion
The geometric mean provides a powerful tool for calculating averages in situations where multiplicative relationships are prevalent. Its applications span finance, biology, engineering, and numerous other fields. While it has limitations, understanding its principles and applications empowers us to analyze data more comprehensively and accurately, making it a valuable asset in the statistical toolkit. By carefully considering the nature of the data and the desired outcome, you can choose the appropriate average – be it the geometric mean, arithmetic mean, or other statistical measures – to provide the most meaningful representation of the data at hand. Remember, correctly interpreting statistical results relies heavily on understanding the underlying methods and their limitations.
Latest Posts
Latest Posts
-
Aquellos Sombreros Son Muy Elegantes 1 Of 1
Jun 06, 2025
-
Carpal Tunnel Syndrome Is Not Very Common Among Licensees
Jun 06, 2025
-
Which Of The Following Values Are In The Range
Jun 06, 2025
-
0 727935 Rounded To The Nearest Thousandths Place Is
Jun 06, 2025
-
What Is The Shape Of The Indian Shawl
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Find The Geometric Mean Of 8 And 28. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.