Find Z If 1 4/11 Of Z Is 45
Breaking News Today
Jun 01, 2025 · 4 min read
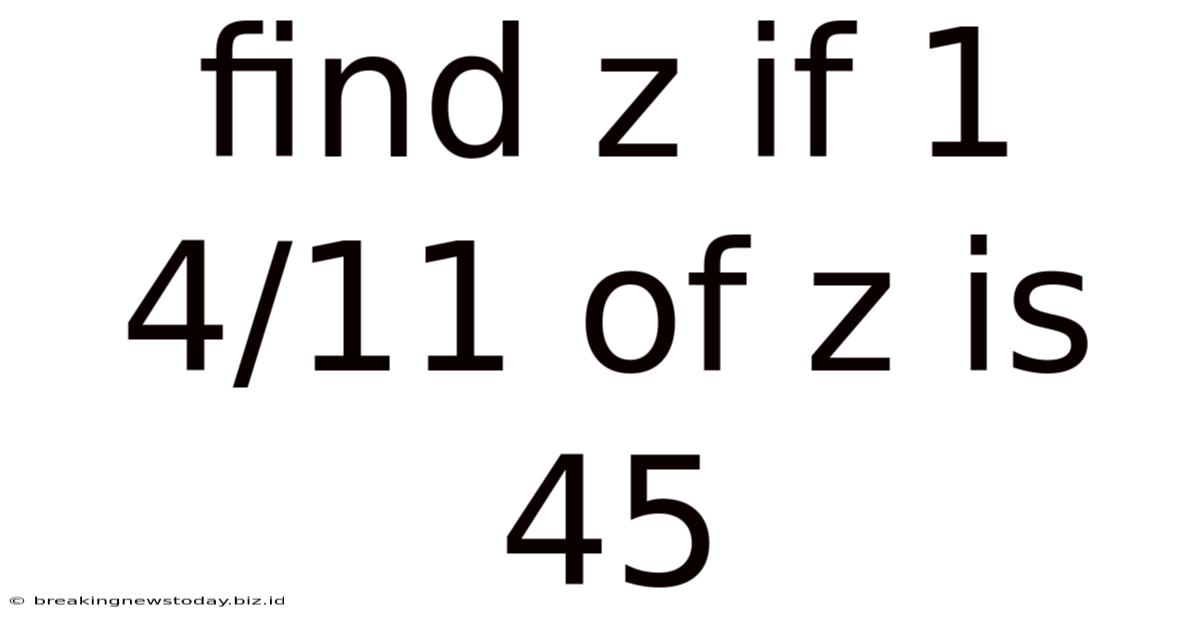
Table of Contents
Find Z if 1 4/11 of Z is 45: A Comprehensive Guide to Solving Fraction Equations
This article provides a comprehensive guide on how to solve the equation "1 4/11 of z is 45," covering various approaches and explaining the underlying mathematical concepts. We'll delve into different methods of solving this type of problem, including converting mixed numbers to improper fractions, applying the multiplicative inverse, and verifying the solution. Furthermore, we will explore the broader context of solving fraction equations and their applications in various fields.
Understanding the Problem: Deconstructing "1 4/11 of z is 45"
The statement "1 4/11 of z is 45" can be translated into a mathematical equation. The phrase "of" signifies multiplication. Therefore, the equation becomes:
(1 4/11) * z = 45
Our goal is to isolate 'z' and find its value. To achieve this, we need to manipulate the equation using fundamental algebraic principles.
Method 1: Converting to Improper Fractions
The first step involves converting the mixed number 1 4/11 into an improper fraction. This makes the calculations easier and more straightforward.
To convert 1 4/11 to an improper fraction, we multiply the whole number (1) by the denominator (11), add the numerator (4), and keep the same denominator:
(1 * 11) + 4 = 15
So, 1 4/11 becomes 15/11.
Now our equation becomes:
(15/11) * z = 45
Method 2: Applying the Multiplicative Inverse (Reciprocal)
To solve for 'z', we need to isolate it. We can do this by multiplying both sides of the equation by the multiplicative inverse (reciprocal) of 15/11, which is 11/15. The multiplicative inverse of a fraction is obtained by flipping the numerator and the denominator.
Multiplying both sides by 11/15:
(11/15) * (15/11) * z = 45 * (11/15)
Notice that (11/15) * (15/11) simplifies to 1. This leaves us with:
z = 45 * (11/15)
Method 3: Simplifying and Solving for Z
Now we can simplify and solve for z:
We can simplify the expression by canceling out common factors between 45 and 15:
45 ÷ 15 = 3
So the equation becomes:
z = 3 * 11
Therefore:
z = 33
Verifying the Solution
To ensure our solution is correct, we can substitute z = 33 back into the original equation:
(1 4/11) * 33 = 45
Converting 1 4/11 to an improper fraction (15/11):
(15/11) * 33 = 45
Simplifying:
15 * 3 = 45
45 = 45
Since the equation holds true, our solution z = 33 is correct.
Expanding the Understanding: Solving Fraction Equations in General
The problem we've solved is a specific example of a broader class of problems involving fraction equations. Solving these types of equations consistently involves a few key steps:
-
Convert Mixed Numbers to Improper Fractions: As we saw, this simplifies the equation and makes calculations easier.
-
Isolate the Variable: This usually involves using the multiplicative inverse, but other algebraic manipulations might be needed depending on the complexity of the equation.
-
Simplify and Solve: After isolating the variable, perform any necessary simplifications and calculations to find the value of the variable.
-
Verify the Solution: Always substitute the solution back into the original equation to confirm its accuracy. This step is crucial in avoiding errors and building confidence in your answer.
Applications of Fraction Equations in Real-World Scenarios
Fraction equations aren't just abstract mathematical concepts; they have numerous practical applications in various fields:
-
Construction and Engineering: Calculating material quantities, proportions, and scaling dimensions frequently involve fraction equations. For example, determining the amount of cement needed for a particular concrete mix.
-
Cooking and Baking: Recipes often use fractions to specify ingredient amounts. Adjusting recipes to serve more or fewer people requires solving fraction equations.
-
Finance: Calculating interest, discounts, and proportions of investments often involve solving equations containing fractions.
-
Science: Many scientific formulas and calculations use fractions and ratios, requiring the ability to solve fraction equations.
Beyond the Basics: More Complex Fraction Equations
While the example we worked through was relatively straightforward, fraction equations can become more complex. They may involve multiple variables, more intricate fractions, or require multiple steps to solve. For example, you might encounter equations like:
(2/3)x + (1/4)y = 5
(1/2)x - (3/5)y = 2
Solving these requires utilizing systems of equations and employing methods like substitution or elimination.
Mastering Fraction Equations: Tips and Practice
To truly master solving fraction equations, consistent practice is essential. Work through various examples, starting with simpler equations and gradually progressing to more complex ones. Familiarize yourself with different methods of solving these equations, including the use of the multiplicative inverse, and choose the method that best suits each problem. Don't be afraid to use online resources and calculators to check your answers and identify areas where you need improvement.
Conclusion: Confidence in Solving Fraction Equations
Solving equations involving fractions might seem daunting at first, but with a systematic approach and consistent practice, you can build confidence and proficiency in this crucial mathematical skill. By understanding the fundamental principles, converting mixed numbers to improper fractions, utilizing the multiplicative inverse, and verifying your solutions, you can successfully tackle even the most challenging fraction equations. Remember that understanding the underlying principles and practicing regularly are keys to mastering this important mathematical skill and applying it in various real-world scenarios.
Latest Posts
Latest Posts
-
King Lear Is A Circa 1606
Jun 03, 2025
-
Which Phrase From The Haiku Reveals The Idea Of Renewal
Jun 03, 2025
-
Plot And Label The Following Points
Jun 03, 2025
-
Many Academic Disciplines Have Their Own Style Manual
Jun 03, 2025
-
Who Regulates Access To Electrical Closets
Jun 03, 2025
Related Post
Thank you for visiting our website which covers about Find Z If 1 4/11 Of Z Is 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.