Fiona Wrote The Linear Equation Y 2 5x 5
Breaking News Today
Jun 06, 2025 · 6 min read
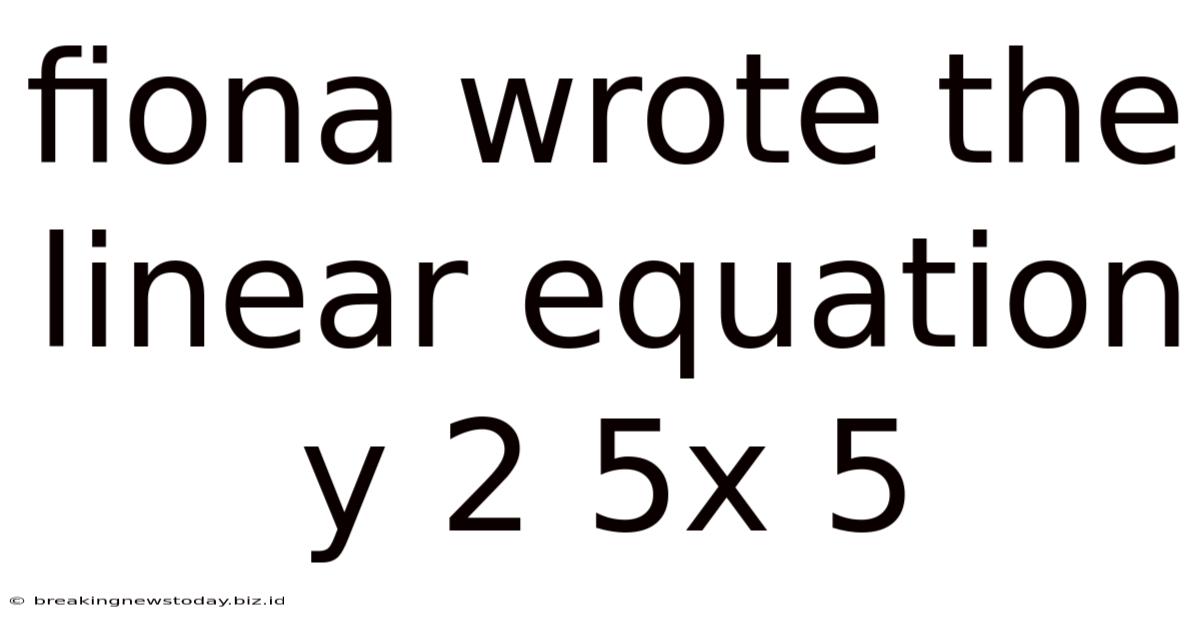
Table of Contents
Fiona Wrote the Linear Equation: y = 2/5x + 5 – A Deep Dive into Linear Equations
Fiona's linear equation, y = (2/5)x + 5, opens a door to a world of mathematical concepts and applications. This seemingly simple equation holds the key to understanding fundamental principles of algebra, geometry, and even real-world scenarios. Let's delve into a comprehensive exploration of this equation, examining its components, graphical representation, practical applications, and the broader context of linear equations in mathematics.
Understanding the Components of Fiona's Equation
The equation y = (2/5)x + 5 is a classic example of a linear equation in slope-intercept form. This form is represented as y = mx + b, where:
- y represents the dependent variable. Its value depends on the value of x.
- x represents the independent variable. Its value is chosen freely.
- m represents the slope of the line. This indicates the steepness and direction of the line. A positive slope means the line rises from left to right, while a negative slope means it falls.
- b represents the y-intercept. This is the point where the line intersects the y-axis (where x = 0).
In Fiona's equation, we can identify the components as follows:
- m = 2/5: This is the slope. The line rises 2 units for every 5 units it moves to the right.
- b = 5: This is the y-intercept. The line crosses the y-axis at the point (0, 5).
Significance of the Slope (m = 2/5)
The slope of 2/5 reveals crucial information about the relationship between x and y. It signifies a positive correlation: as x increases, y also increases. The value itself indicates a relatively gentle incline. A steeper slope would have a larger numerical value (e.g., 2, 5, or even larger), while a flatter slope would have a smaller value (e.g., 1/10, 1/2).
Significance of the Y-Intercept (b = 5)
The y-intercept of 5 indicates that when x is zero, y has a value of 5. This is a critical point on the line and serves as the starting point for graphing the equation. The y-intercept often represents an initial value or a baseline in real-world applications.
Graphing Fiona's Linear Equation
Visualizing the equation through a graph provides a clearer understanding of its behavior. To graph y = (2/5)x + 5:
-
Plot the y-intercept: Begin by plotting the point (0, 5) on the coordinate plane.
-
Use the slope to find another point: Since the slope is 2/5, move 5 units to the right and 2 units up from the y-intercept. This gives you the point (5, 7).
-
Draw the line: Draw a straight line through the two points (0, 5) and (5, 7). This line represents all the possible solutions to the equation y = (2/5)x + 5.
Interpreting the Graph
The graph visually displays the linear relationship between x and y. Any point on the line satisfies the equation. Points not on the line do not satisfy the equation. The graph provides an immediate understanding of how y changes with changes in x, reflecting the positive correlation dictated by the positive slope.
Real-World Applications of Linear Equations
Linear equations are remarkably versatile and find applications in numerous real-world scenarios. Fiona's equation, while simple, can be adapted to model various situations. Consider the following examples:
-
Cost Calculation: Imagine a taxi service where the initial fare is $5 (y-intercept) and the cost per kilometer is $0.40 (2/5 of a dollar, adjusted for simplicity). The equation y = 0.4x + 5 could then represent the total cost (y) based on the distance traveled (x).
-
Temperature Conversion: Linear equations can be used to convert between different temperature scales. While not a direct representation of Fiona's equation, the principle remains the same.
-
Sales Projections: Businesses often use linear equations to project sales based on trends. If sales have been steadily increasing at a consistent rate, a linear equation can be used to predict future sales.
-
Physics and Engineering: Linear equations are fundamental in physics and engineering for modeling motion, forces, and other physical phenomena.
Extending the Understanding: Other Forms of Linear Equations
While Fiona's equation is presented in slope-intercept form, linear equations can also be represented in other forms:
- Standard Form: Ax + By = C, where A, B, and C are constants.
- Point-Slope Form: y - y1 = m(x - x1), where (x1, y1) is a point on the line and m is the slope.
Converting between these forms is a valuable skill in algebra, allowing for flexibility in solving problems and analyzing data. For example, Fiona's equation could be converted to standard form through simple algebraic manipulation.
Solving Problems Using Fiona's Equation
Fiona's equation provides a framework for solving various problems. For instance:
-
Finding y given x: If x = 10, substitute this value into the equation: y = (2/5)(10) + 5 = 9. This means when x is 10, y is 9.
-
Finding x given y: If y = 10, solve the equation for x: 10 = (2/5)x + 5. Subtract 5 from both sides, then multiply by 5/2 to find x = 12.5.
-
Determining if a point lies on the line: To check if the point (15, 11) lies on the line, substitute x = 15 into the equation: y = (2/5)(15) + 5 = 11. Since this matches the y-coordinate, the point does lie on the line.
These examples highlight the equation's utility in calculating corresponding values and verifying points.
Beyond the Basics: Systems of Linear Equations
Fiona's equation can also be used in the context of systems of linear equations. This involves solving multiple linear equations simultaneously to find solutions that satisfy all equations. Graphical solutions involve identifying the intersection point of multiple lines on a coordinate plane. Algebraic methods, such as substitution or elimination, offer another approach to solve these systems. Understanding systems of equations allows for the analysis of more complex relationships and scenarios.
Applications in Data Analysis and Regression
Linear equations are crucial in data analysis and regression. When dealing with data that exhibits a linear trend, a linear equation can be used to model the relationship between variables. This process, known as linear regression, involves finding the line of best fit that minimizes the overall error between the data points and the line. This technique provides a valuable tool for making predictions and understanding correlations within data sets.
Conclusion: The Power of a Simple Linear Equation
Fiona's equation, y = (2/5)x + 5, might appear simple at first glance. However, a deeper examination reveals its rich mathematical significance and widespread applicability. From understanding fundamental algebraic concepts to solving real-world problems and analyzing data, this equation serves as a powerful foundation for more advanced mathematical studies and practical applications. Its simplicity belies its profound influence on various fields, emphasizing the importance of mastering the fundamentals of linear equations. By grasping the components, graphing techniques, and problem-solving methods associated with this equation, one can unlock a wider understanding of mathematics and its role in interpreting and modeling the world around us.
Latest Posts
Latest Posts
-
Which Word Suggests The Greatest Power
Jun 06, 2025
-
What Is The Length Of Side Ab Of Parallelogram Abcd
Jun 06, 2025
-
Give Three Observations That Can Be Made From The Graph
Jun 06, 2025
-
What Is The Least Common Product Marketing Technique
Jun 06, 2025
-
Identify Which Sphere Of Earth Each Image Represents
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Fiona Wrote The Linear Equation Y 2 5x 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.