Five And Twenty-two Thousandths As A Decimal
Breaking News Today
Jun 04, 2025 · 5 min read
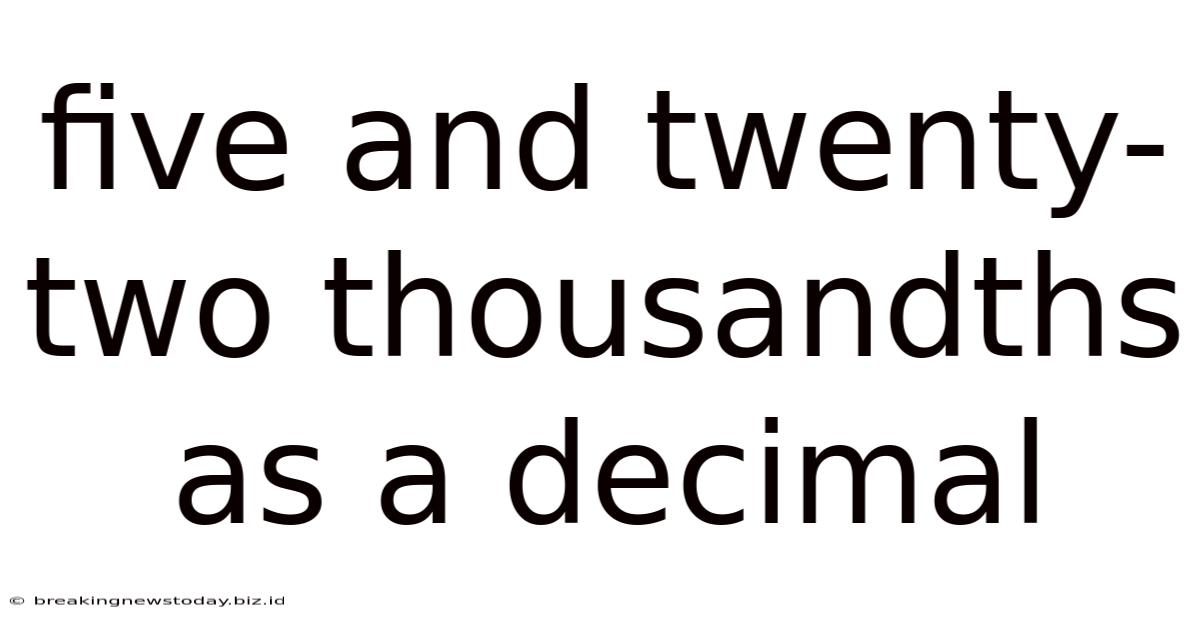
Table of Contents
Five and Twenty-two Thousandths as a Decimal: A Comprehensive Guide
Understanding decimal representation is fundamental in mathematics and its applications across various fields. This article delves deep into representing the number "five and twenty-two thousandths" as a decimal, exploring the underlying concepts, practical applications, and related mathematical operations. We will cover this seemingly simple topic in detail, demonstrating its significance and offering various perspectives for a complete understanding.
Decimals: A Foundation of Numerical Representation
Decimals are a crucial part of our number system, enabling us to express numbers that fall between whole numbers. They extend the power of whole numbers by allowing for the representation of fractions and proportions with ease. A decimal number consists of two parts:
- The whole number part: This represents the number of whole units.
- The fractional part: This is expressed to the right of a decimal point (.), representing parts of a whole. Each place value to the right of the decimal point represents decreasing powers of 10: tenths, hundredths, thousandths, ten-thousandths, and so on.
Understanding place value is key to converting numbers from words to decimals and vice versa.
Decoding "Five and Twenty-two Thousandths"
The phrase "five and twenty-two thousandths" clearly indicates a mixed number, combining a whole number component and a fractional component. Let's break it down:
- Five: This represents the whole number part, indicating five complete units.
- And: This word signifies the separation between the whole number and the fractional part.
- Twenty-two thousandths: This is the fractional part, meaning 22 out of 1000 equal parts.
To represent this as a decimal, we write the whole number part followed by a decimal point, then the fractional part. Since the fractional part is "twenty-two thousandths," it occupies the thousandths place (three digits after the decimal point).
Therefore, "five and twenty-two thousandths" as a decimal is 5.022.
Place Value and Decimal Representation
Let's solidify our understanding by examining the place value of each digit in 5.022:
- 5: Ones place (5 × 1 = 5)
- 0: Tenths place (0 × 0.1 = 0)
- 2: Hundredths place (2 × 0.01 = 0.02)
- 2: Thousandths place (2 × 0.001 = 0.002)
Summing these values: 5 + 0 + 0.02 + 0.002 = 5.022
From Fractions to Decimals
The number "five and twenty-two thousandths" can also be expressed as a mixed fraction: 5 <sup>22</sup>⁄<sub>1000</sub>. Converting this mixed fraction to a decimal involves dividing the numerator (22) by the denominator (1000):
22 ÷ 1000 = 0.022
Adding the whole number part (5), we get 5.022, confirming our earlier conversion.
This demonstrates the interchangeable nature of fractions and decimals; they both represent the same numerical value, albeit with different notations.
Practical Applications of Decimal Representation
Decimal representation finds extensive applications in various aspects of life:
1. Financial Transactions:
Decimals are ubiquitous in finance, representing currency values, interest rates, and stock prices. For example, $5.022 represents a monetary value. The precision offered by decimals is essential for accurate financial calculations.
2. Scientific Measurements:
Scientific measurements often involve decimal numbers to express precise values. Measurements of length, weight, volume, and temperature frequently utilize decimals to convey high accuracy. For instance, 5.022 meters represents a length measurement.
3. Engineering and Technology:
Engineering designs and technological advancements rely heavily on decimals for precise calculations and specifications. Decimal precision is crucial in creating intricate components and systems.
4. Data Analysis and Statistics:
Decimal numbers are central to data analysis and statistics. Representing data with decimals allows for greater accuracy and detailed analysis, leading to more informative results.
5. Everyday Life:
Even in everyday activities, decimals are used constantly. Examples include measuring ingredients for cooking, calculating distances, and even expressing time.
Mathematical Operations with Decimals
Understanding decimal representation is essential for performing various mathematical operations:
1. Addition and Subtraction:
Adding and subtracting decimals involves aligning the decimal points and then performing the operation as with whole numbers.
Example: 5.022 + 2.345 = 7.367
2. Multiplication and Division:
Multiplying decimals involves multiplying the numbers as whole numbers and then placing the decimal point in the result based on the total number of decimal places in the original numbers. Division of decimals involves converting the divisor to a whole number by multiplying both the divisor and dividend by the appropriate power of 10, then performing the division.
Example: 5.022 × 2 = 10.044 Example: 5.022 ÷ 2 = 2.511
Rounding Decimals
Often, decimals need to be rounded to a specific number of decimal places for simplification or due to limitations in measurement precision. Rounding involves examining the digit to the right of the desired decimal place:
- If this digit is 5 or greater, the preceding digit is rounded up.
- If this digit is less than 5, the preceding digit remains unchanged.
For instance, rounding 5.022 to one decimal place would result in 5.0, while rounding to two decimal places would give 5.02.
Expanding on the Concept: Beyond Thousandths
While this article focuses on "five and twenty-two thousandths," the principles extend to numbers expressed in ten-thousandths, hundred-thousandths, and beyond. The key is understanding the place value system and how it relates to the powers of 10. Each position to the right of the decimal point represents a progressively smaller fraction of one.
Conclusion: Mastering Decimal Representation
Understanding how to represent "five and twenty-two thousandths" as a decimal, 5.022, is not merely a matter of rote memorization; it’s about grasping the fundamental principles of place value, fractional representation, and the practical applications of decimals in various fields. This article has explored these principles in detail, offering a comprehensive understanding of decimal numbers and their importance in both mathematical operations and real-world applications. From finance and science to everyday life, the ability to confidently work with decimals is a valuable skill that enhances mathematical literacy and problem-solving abilities. Mastering this skill lays the groundwork for further exploration of advanced mathematical concepts and their applications.
Latest Posts
Latest Posts
-
As Ar 4s23d104p3 Ar 4s23d104p2 Kr 4s24d104p3 Kr 4s23d104p3
Jun 05, 2025
-
A Customer With A Product Centric Mindset Might Think
Jun 05, 2025
-
Air Conditioning And Refrigeration Reversible Ratchet Wrenches Are Used To
Jun 05, 2025
-
In Gardners Grendel How Does Grendel Classify Humans
Jun 05, 2025
-
What Differentiates Baseline Activities From Health Enhancing Activities
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about Five And Twenty-two Thousandths As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.