Five Less Than A Number Is Greater Than Twenty
Breaking News Today
Jun 04, 2025 · 5 min read
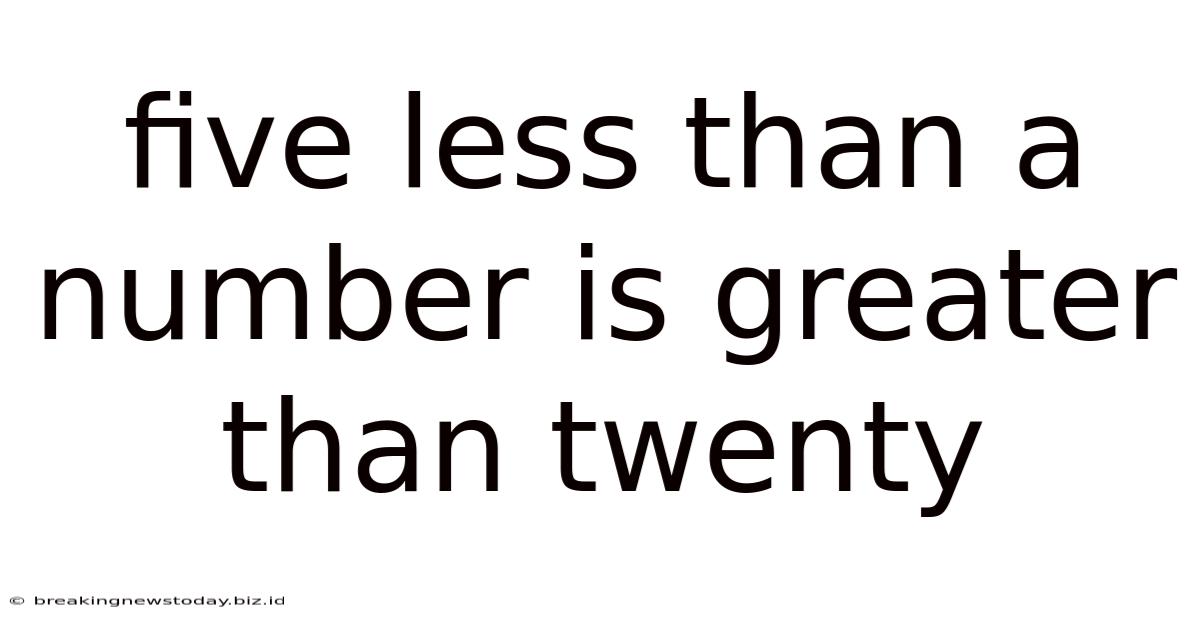
Table of Contents
Five Less Than a Number is Greater Than Twenty: A Comprehensive Exploration
This seemingly simple statement, "five less than a number is greater than twenty," opens a door to a fascinating world of mathematical concepts and problem-solving techniques. While the core idea might seem elementary, understanding its nuances and exploring its applications reveals a deeper appreciation for algebra and its real-world implications. This article will delve into this inequality, exploring its solution, graphical representation, and extensions into more complex scenarios. We'll also look at how to effectively communicate mathematical concepts and explain the reasoning behind the solutions.
Understanding the Inequality: "Five Less Than a Number is Greater Than Twenty"
The statement itself can be translated directly into a mathematical inequality. Let's represent the unknown "number" with the variable 'x'. The phrase "five less than a number" translates to x - 5. The phrase "is greater than twenty" translates to > 20. Therefore, the complete inequality is:
x - 5 > 20
This inequality signifies that there's a range of values for 'x' that satisfy the condition. It's not a single solution but a set of solutions. Finding these solutions forms the basis of solving this mathematical problem.
Solving the Inequality: Finding the Range of Solutions
To solve for 'x', we need to isolate the variable on one side of the inequality sign. We can achieve this using basic algebraic manipulation. The key principle is that any operation performed on one side of the inequality must also be performed on the other, maintaining the inequality's integrity.
-
Add 5 to both sides: Adding 5 to both sides of the inequality cancels out the -5 on the left side, giving us:
x - 5 + 5 > 20 + 5This simplifies to:
x > 25
This solution tells us that any number greater than 25 satisfies the original statement. 'x' can be 26, 27, 25.1, 1000 – any value exceeding 25. This is a crucial understanding; the solution isn't a single point but an infinite set of numbers.
Visualizing the Solution: Graphical Representation
Inequalities are often best understood through their graphical representations. We can visualize the solution x > 25 on a number line:
[Imagine a number line here with an open circle at 25 and an arrow pointing to the right, indicating all numbers greater than 25.]
The open circle at 25 indicates that 25 itself is not included in the solution set, as the inequality is strictly greater than (>), not greater than or equal to (≥). The arrow pointing to the right shows that all numbers to the right of 25 are part of the solution.
This graphical representation provides a clear and intuitive understanding of the range of values satisfying the inequality. It’s a powerful tool for visualizing mathematical concepts and communicating solutions effectively.
Extending the Concept: Variations and Applications
The basic inequality "five less than a number is greater than twenty" can be extended and modified to explore a wider range of mathematical concepts:
1. Introducing "Equal To"
What if the statement was "five less than a number is greater than or equal to twenty"? This changes the inequality to:
x - 5 ≥ 20
Following the same steps as before, we add 5 to both sides:
x ≥ 25
The solution now includes 25 itself, as indicated by the "≥" symbol. Graphically, this would be represented by a closed circle at 25 on the number line, showing that 25 is included in the solution set.
2. Introducing a Second Variable
Let's introduce a second variable, say 'y', into the equation. Suppose the statement is: "Five less than a number (x) is greater than twice another number (y)." This can be written as:
x - 5 > 2y
This inequality has infinitely many solutions, as any pair of x and y values satisfying the condition will work. To find specific solutions, we would need additional constraints or information. For example, we might be given a value for either x or y, allowing us to solve for the other variable.
3. Real-World Applications
Inequalities like this frequently appear in real-world scenarios. Consider a scenario where a salesperson needs to make at least $20,000 in commission this month. They earn $5000 base salary and make $5 for each item sold (x). Then the inequality representing this would be:
5000 + 5x ≥ 20000
Solving for x will tell them how many items they need to sell to meet their target.
This kind of inequality is fundamental in various fields including:
- Finance: Budgeting, investment analysis, loan calculations.
- Engineering: Determining load limits, material specifications.
- Computer Science: Resource allocation, algorithm efficiency.
- Physics: Analyzing forces, energy calculations.
Understanding how to solve and interpret inequalities is essential in these areas.
Communicating Mathematical Reasoning: Clear and Concise Explanations
Communicating mathematical reasoning effectively is crucial for both understanding and teaching mathematical concepts. When presenting solutions, follow these best practices:
-
State the Problem Clearly: Begin by restating the problem in your own words to ensure understanding.
-
Show Your Work: Detail each step of your calculations, explaining the reasoning behind each operation. This transparency helps readers follow the logic.
-
Use Proper Notation: Employ accurate mathematical symbols and notations consistently throughout the solution.
-
Explain Your Reasoning: Don't just provide the answer; explain the underlying principles and logic that led to the solution. This is particularly important for inequalities, where understanding the range of solutions is key.
-
Check Your Answer: Verify your solution by plugging it back into the original inequality. This helps identify potential errors and strengthens the confidence in the result.
-
Use Visual Aids: Diagrams, graphs, and number lines can significantly enhance understanding, especially for visual learners.
By consistently applying these communication strategies, you can make your mathematical explanations clear, concise, and easily understood by a wider audience.
Conclusion: The Significance of Simple Inequalities
The inequality "five less than a number is greater than twenty" might seem simplistic, but it serves as a robust foundation for grasping fundamental concepts in algebra and inequality solving. Its practical applications extend to diverse fields, highlighting the importance of understanding and interpreting mathematical inequalities. By mastering the techniques presented here, you'll be better equipped to tackle more complex mathematical problems and to effectively communicate your solutions, laying a strong foundation for further mathematical exploration. The ability to translate real-world problems into mathematical expressions and interpret the solutions is a valuable skill applicable to various aspects of life. Remember the importance of clear communication, visualization, and a thorough understanding of the underlying principles.
Latest Posts
Latest Posts
-
Samuel Was Preparing For The Triathlon
Jun 06, 2025
-
Ralph Peer Recorded All Of These Musicians Except
Jun 06, 2025
-
Jim Had A Bag Of Coins
Jun 06, 2025
-
Impaired Driving Is The Countrys Most Frequently Committed
Jun 06, 2025
-
1 1 Additional Practice Measuring Segments And Angles
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about Five Less Than A Number Is Greater Than Twenty . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.