Gcf Of 38 76 And 114
Breaking News Today
Jun 07, 2025 · 5 min read
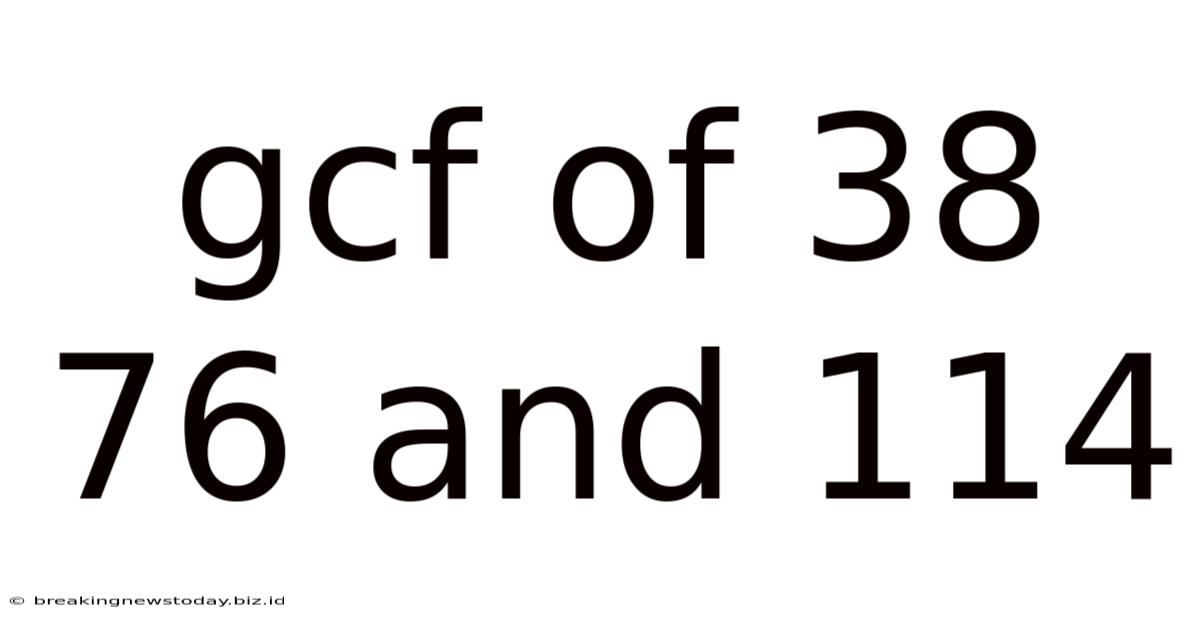
Table of Contents
Finding the Greatest Common Factor (GCF) of 38, 76, and 114: A Comprehensive Guide
Determining the greatest common factor (GCF), also known as the greatest common divisor (GCD), of a set of numbers is a fundamental concept in mathematics with applications ranging from simplifying fractions to solving complex algebraic problems. This article will delve into the process of finding the GCF of 38, 76, and 114, exploring various methods and providing a deeper understanding of the underlying principles. We’ll go beyond simply stating the answer, focusing on the how and why, equipping you with the skills to tackle similar problems with confidence.
Understanding the Greatest Common Factor (GCF)
Before we jump into calculating the GCF of 38, 76, and 114, let's solidify our understanding of the concept. The GCF of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. Think of it as the largest common divisor shared by all the numbers in the set. For instance, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
Method 1: Prime Factorization
The prime factorization method is a robust and reliable technique for finding the GCF of any set of numbers. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves. Let's apply this to our numbers: 38, 76, and 114.
Prime Factorization of 38:
38 = 2 x 19
Prime Factorization of 76:
76 = 2 x 2 x 19 = 2² x 19
Prime Factorization of 114:
114 = 2 x 3 x 19
Identifying the Common Factors:
Now, we look for the prime factors that are common to all three numbers. In this case, we see that both 2 and 19 are present in the prime factorization of each number.
Calculating the GCF:
To find the GCF, we multiply the common prime factors together:
GCF(38, 76, 114) = 2 x 19 = 38
Therefore, the greatest common factor of 38, 76, and 114 is 38.
Method 2: Listing Factors
This method is suitable for smaller numbers and involves listing all the factors of each number and then identifying the largest common factor.
Factors of 38:
1, 2, 19, 38
Factors of 76:
1, 2, 4, 19, 38, 76
Factors of 114:
1, 2, 3, 6, 19, 38, 57, 114
Identifying the Common Factors:
By comparing the lists, we can see that the common factors of 38, 76, and 114 are 1, 2, 19, and 38.
Determining the GCF:
The largest of these common factors is 38, confirming our result from the prime factorization method.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until we reach a point where the two numbers are equal. That number is the GCF. Let's apply this to our numbers sequentially.
First, let's find the GCF of 38 and 76:
- 76 = 2 * 38 + 0 (The remainder is 0, meaning 38 divides 76 evenly)
The GCF of 38 and 76 is 38.
Now, let's find the GCF of 38 and 114:
- 114 = 3 * 38 + 0 (The remainder is 0, meaning 38 divides 114 evenly)
The GCF of 38 and 114 is 38.
Since the GCF of 38 and 76 is 38 and the GCF of 38 and 114 is 38, the GCF of 38, 76, and 114 is 38.
Applications of Finding the GCF
Understanding and applying the GCF has practical applications in various mathematical contexts:
-
Simplifying Fractions: The GCF allows us to reduce fractions to their simplest form. For example, the fraction 76/114 can be simplified by dividing both the numerator and denominator by their GCF (38), resulting in the equivalent fraction 2/3.
-
Solving Algebraic Equations: GCF plays a role in factoring algebraic expressions, making it easier to solve equations and simplify complex expressions.
-
Real-World Problems: Problems involving dividing quantities into equal groups often require finding the GCF to determine the maximum number of groups possible. For example, if you have 38 red marbles, 76 blue marbles, and 114 green marbles, and you want to divide them into identical bags with the same number of each color, you could find the GCF (38) to determine that you can make 38 identical bags.
-
Number Theory: GCF is a fundamental concept in number theory, a branch of mathematics that studies integers and their properties. It's used in various advanced theorems and proofs.
Choosing the Right Method
The best method for finding the GCF depends on the size and nature of the numbers involved:
-
Prime Factorization: Best for smaller numbers where prime factors are readily identifiable.
-
Listing Factors: Suitable only for very small numbers, as it becomes cumbersome for larger numbers.
-
Euclidean Algorithm: The most efficient method for larger numbers, offering a systematic approach to finding the GCF.
Conclusion
Finding the greatest common factor is a crucial skill in mathematics. This article has explored three distinct methods – prime factorization, listing factors, and the Euclidean algorithm – for determining the GCF of 38, 76, and 114. We've demonstrated that the GCF of these three numbers is 38, and we've highlighted the practical applications of this concept across various mathematical domains and real-world scenarios. By understanding these methods and their applications, you’ll be well-equipped to tackle GCF problems with confidence and efficiency. Remember to choose the most appropriate method based on the numbers involved to optimize your calculation process.
Latest Posts
Latest Posts
-
Which Sentence Is True About Abstaining From Sex
Jun 07, 2025
-
Which Statements Accurately Compare Beowulf And Grendel Select 2 Options
Jun 07, 2025
-
Which Statement Best Sums Up The Meaning Of Jesuss Words
Jun 07, 2025
-
Which Concept Best Summarizes The Beliefs Of Ashoka
Jun 07, 2025
-
Which Table Represents A Linear Function I Ready
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 38 76 And 114 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.