Given Wxyz Is A Parallelogram Zx Wy
Breaking News Today
Jun 06, 2025 · 5 min read
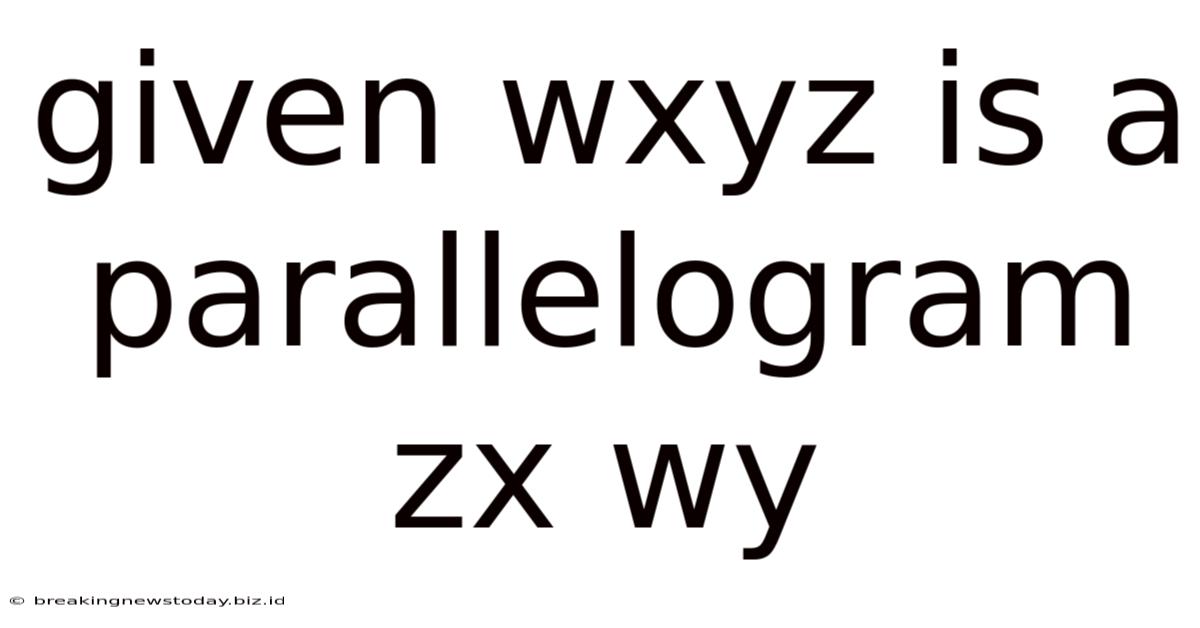
Table of Contents
Parallelogram WXYZ: Exploring its Properties and Applications
A parallelogram, a fundamental geometric shape, holds a significant place in mathematics and its applications. Defined by its opposite sides being parallel and equal in length, parallelograms exhibit several unique properties that make them crucial in various fields, from architecture and engineering to computer graphics and game design. This comprehensive article delves deep into the characteristics of parallelogram WXYZ, specifically focusing on the implications of its diagonal properties (ZX and WY), exploring proofs, related theorems, and real-world applications.
Understanding the Parallelogram: Key Definitions and Properties
Before we embark on a detailed analysis of parallelogram WXYZ, let's establish a firm understanding of the foundational concepts.
Definition: A parallelogram is a quadrilateral (a four-sided polygon) with both pairs of opposite sides parallel.
Key Properties: Parallelograms possess several inherent properties:
- Opposite sides are equal in length: This means that WX = YZ and XY = WZ.
- Opposite angles are equal: This means that ∠W = ∠Y and ∠X = ∠Z.
- Consecutive angles are supplementary: This means that ∠W + ∠X = 180°, ∠X + ∠Y = 180°, ∠Y + ∠Z = 180°, and ∠Z + ∠W = 180°.
- Diagonals bisect each other: This crucial property states that the diagonals of a parallelogram intersect at a point where they are divided into two equal halves. This is where the diagonals ZX and WY of parallelogram WXYZ become especially relevant.
The Significance of Diagonals ZX and WY
The diagonals ZX and WY play a vital role in determining various properties of parallelogram WXYZ. Their intersection point, let's call it 'O', creates a unique relationship between the parallelogram's sides and angles. This intersection point effectively divides each diagonal into two congruent segments.
- ZX = ZO + OX and WY = WO + OY and ZO = OX and WO = OY.
This bisecting property is critical in various proofs and applications. We will explore these in detail in the subsequent sections.
Proving Properties of Parallelogram WXYZ using its Diagonals
We can leverage the properties of the diagonals ZX and WY to prove various characteristics of parallelogram WXYZ. Let's explore some of these proofs:
Proof 1: Opposite Sides are Equal
Theorem: In parallelogram WXYZ, WX = YZ and XY = WZ.
Proof:
- Construct: Draw the diagonals ZX and WY, intersecting at point O.
- Triangles: Consider triangles ΔWOX and ΔZOY.
- Congruence: WO = OY (diagonals bisect each other) and ZO = OX (diagonals bisect each other). ∠WOX = ∠ZOY (vertically opposite angles).
- SAS Congruence: By the Side-Angle-Side (SAS) congruence criterion, ΔWOX ≅ ΔZOY.
- Conclusion: Since corresponding parts of congruent triangles are equal, WX = YZ. Similarly, by considering triangles ΔWOY and ΔZOX, we can prove XY = WZ.
Proof 2: Opposite Angles are Equal
Theorem: In parallelogram WXYZ, ∠W = ∠Y and ∠X = ∠Z.
Proof:
- Construct: Draw the diagonals ZX and WY, intersecting at point O.
- Triangles: Consider triangles ΔWOX and ΔYOZ.
- Congruence: Using the same logic as in Proof 1 (SAS congruence), we can establish ΔWOX ≅ ΔYOZ.
- Conclusion: Therefore, ∠W = ∠Y (corresponding angles of congruent triangles). Similarly, considering triangles ΔWOY and ΔXOZ, we can prove that ∠X = ∠Z.
Proof 3: Consecutive Angles are Supplementary
Theorem: In parallelogram WXYZ, ∠W + ∠X = 180°, ∠X + ∠Y = 180°, ∠Y + ∠Z = 180°, and ∠Z + ∠W = 180°.
Proof:
- Parallel Lines: Since WXYZ is a parallelogram, WX || YZ.
- Transversals: Consider WX and YZ as parallel lines and XY as a transversal.
- Consecutive Interior Angles: ∠W and ∠X are consecutive interior angles, meaning their sum is 180°. Similarly, this holds true for other pairs of consecutive angles.
Special Cases of Parallelograms: Rectangles, Rhombuses, and Squares
Parallelograms encompass a family of shapes with specific properties:
- Rectangle: A rectangle is a parallelogram with four right angles (90°). Its diagonals are equal in length (ZX = WY).
- Rhombus: A rhombus is a parallelogram with four equal sides. Its diagonals are perpendicular bisectors of each other.
- Square: A square is both a rectangle and a rhombus; it has four equal sides and four right angles. Its diagonals are equal in length and perpendicular bisectors of each other.
Applications of Parallelograms
The properties of parallelograms have far-reaching applications in various fields:
- Engineering and Architecture: Parallelograms are used in structural designs, creating stable and balanced structures. The strength and stability of parallelogram-shaped structures are widely utilized in bridges, buildings, and other constructions.
- Computer Graphics and Game Design: Parallelogram-based transformations are essential in computer graphics for rotating, scaling, and shearing images and objects. These transformations are vital for creating realistic and dynamic visuals in video games and simulations.
- Physics: Parallelograms are frequently used in resolving forces and vectors, providing a visual and mathematical framework for analyzing complex physical systems.
- Textile Design: Parallelogram patterns are commonly used in textile and fabric designs, creating visually appealing and geometrically consistent motifs.
Advanced Concepts and Further Exploration
The exploration of parallelograms can extend beyond the basic properties discussed above. Advanced topics include:
- Vector Representation: Parallelograms can be represented using vectors, enabling complex calculations and analysis.
- Area Calculation: Various formulas exist for calculating the area of a parallelogram, utilizing its base, height, and diagonals.
- Coordinate Geometry: Parallelograms can be analyzed using coordinate geometry, allowing for precise calculations of their properties based on their vertices' coordinates.
Conclusion
Parallelogram WXYZ, with its unique properties and the significant role played by its diagonals ZX and WY, serves as a fundamental geometric building block with diverse applications. Understanding its properties is crucial for various fields, from engineering to computer graphics. The proofs and examples discussed in this article aim to provide a comprehensive understanding of this important geometric shape, encouraging further exploration and a deeper appreciation for its mathematical elegance and practical utility. The exploration of special cases of parallelograms and advanced concepts adds another layer of complexity and opens doors to further mathematical investigations. By mastering the fundamental concepts of parallelograms, you can unlock a wider understanding of geometry and its applications in the real world.
Latest Posts
Latest Posts
-
Organized Systems Of Agriculture The Maintenance Of Herds
Jun 07, 2025
-
One Of The Disadvantages Of Aluminum Conduit Is That
Jun 07, 2025
-
Which Theatrical Movement Often Bombards The Viewers Senses
Jun 07, 2025
-
Which Sentence Correctly Uses A Pronoun With A Clear Antecedent
Jun 07, 2025
-
Which Statement About This Dialogue Is True
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about Given Wxyz Is A Parallelogram Zx Wy . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.