How Many 4s Are In 16
Breaking News Today
Jun 05, 2025 · 5 min read
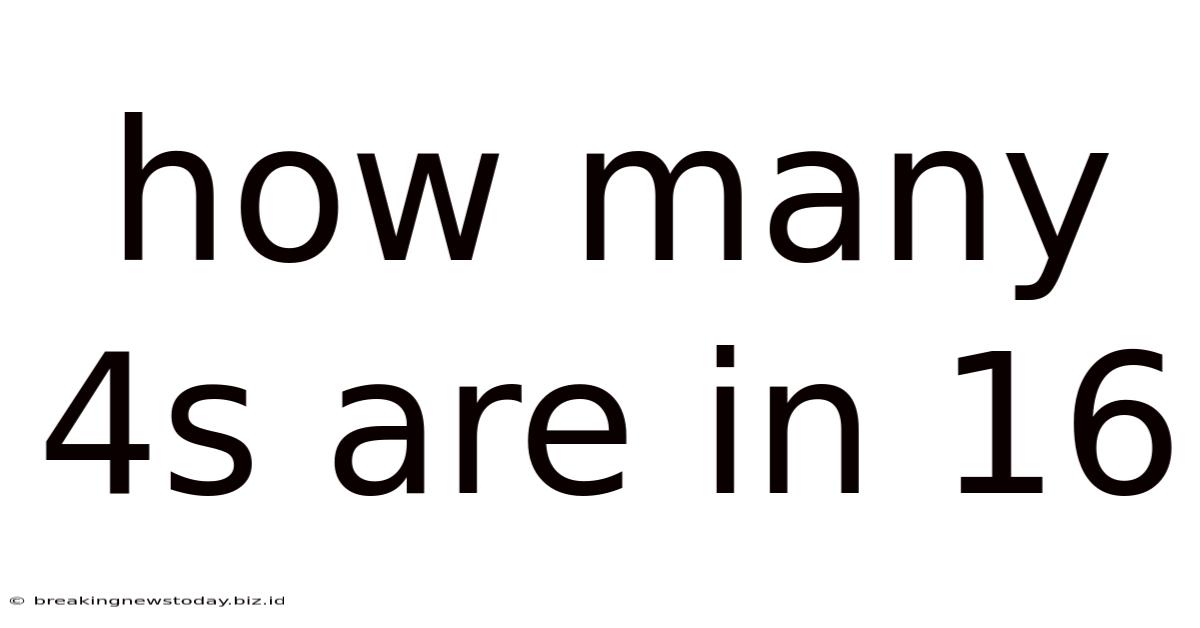
Table of Contents
How Many 4s Are in 16? A Deep Dive into Basic Arithmetic and Beyond
This seemingly simple question, "How many 4s are in 16?", opens a door to a fascinating exploration of fundamental mathematical concepts, their applications, and even some unexpected connections to other fields. While the immediate answer is straightforward, delving deeper reveals a rich tapestry of mathematical understanding.
The Obvious Answer: Division as the Foundation
At its core, the question "How many 4s are in 16?" is a division problem. We're essentially asking how many times the number 4 fits into the number 16. The solution is obtained through simple division:
16 ÷ 4 = 4
Therefore, there are four 4s in 16. This is the bedrock of the answer, easily understood by even young children learning their multiplication tables.
Beyond the Basics: Exploring Different Perspectives
While the direct answer is readily apparent, let's examine this simple arithmetic problem from various angles to highlight its significance and applications:
1. Repeated Addition: A Conceptual Approach
Instead of division, we can approach this from the perspective of repeated addition. How many times do we need to add 4 to itself to reach 16?
4 + 4 + 4 + 4 = 16
Counting the number of 4s in this equation, we again arrive at the answer: four. This method reinforces the fundamental relationship between addition and division.
2. Multiplication: The Inverse Operation
Multiplication and division are inverse operations. This means one undoes the other. If we know that 4 multiplied by 4 equals 16 (4 x 4 = 16), then we inherently know that 16 divided by 4 equals 4. Understanding this inverse relationship is crucial for solving a wide array of mathematical problems.
3. Number Theory: Factors and Multiples
The question also touches upon the concepts of factors and multiples in number theory. 4 is a factor of 16, meaning it divides 16 without leaving a remainder. Conversely, 16 is a multiple of 4, indicating that 16 is a product of 4 and another integer (in this case, 4 itself). Exploring factors and multiples is fundamental to understanding number properties and solving more complex arithmetic problems.
4. Visual Representations: Making it Concrete
For visual learners, representing this problem graphically can be helpful. Imagine four groups of four objects each. Combining these groups gives a total of 16 objects. This visual representation makes the concept of "how many 4s are in 16" tangible and easier to grasp.
Real-World Applications: Where This Simple Concept Shines
The seemingly simple concept of determining how many 4s are in 16 has surprisingly broad applications in various real-world scenarios:
1. Everyday Counting and Grouping
Consider arranging 16 chairs into equal rows. If you want four chairs in each row, how many rows will you need? The answer, derived directly from our understanding of "how many 4s are in 16," is four rows. This simple calculation is essential for countless everyday tasks involving grouping and arrangement.
2. Division of Resources: Fair Shares
Suppose you have 16 cookies and want to share them equally among four friends. Again, the question "how many 4s are in 16?" directly helps determine that each friend receives four cookies. This application highlights the practical use of division in resource allocation and fair distribution.
3. Measurement and Conversion: Units of Measurement
Imagine you have 16 inches of ribbon and need to cut it into 4-inch pieces. How many pieces will you have? The answer is, of course, four. This illustrates how division, stemming from understanding "how many 4s are in 16," is used in measurement conversion and the division of lengths, weights, volumes, and other quantities.
4. Basic Programming and Computer Science
In computer programming, division is a fundamental operation. Understanding how many times a smaller number fits into a larger one is crucial for tasks like array indexing, loop control, and data manipulation. The question "how many 4s are in 16?" directly translates into simple programming logic.
Expanding the Scope: Exploring Related Mathematical Concepts
The simplicity of "how many 4s are in 16?" provides a springboard to explore more advanced mathematical ideas:
1. Prime Factorization: Breaking Down Numbers
While 16 is not a prime number, understanding its factors is crucial in prime factorization. 16 can be factored as 2 x 2 x 2 x 2 (2⁴). This concept is fundamental in number theory and cryptography. The seemingly simple division problem provides a stepping stone to more intricate mathematical concepts.
2. Exponents and Powers: Repeated Multiplication
The factorization of 16 (2⁴) introduces exponents and powers. Understanding exponents is crucial in various scientific and engineering applications, where exponential growth and decay are commonly modeled. The relationship between 4 and 16 provides a concrete example of exponential relationships.
3. Modular Arithmetic: Remainders and Cyclicity
While the division of 16 by 4 leaves no remainder, exploring modular arithmetic involves considering remainders. For instance, if we divide other numbers by 4, the remainder can be 0, 1, 2, or 3. Understanding remainders is essential in various applications like cryptography and computer science.
4. Algebraic Equations: Using Variables
We can represent this problem algebraically: 4x = 16. Solving for 'x' involves the same division as before, demonstrating the connection between arithmetic and algebra. This introduces the power of variables and symbolic representation in mathematical problem-solving.
Conclusion: The Power of Simple Arithmetic
The question "How many 4s are in 16?" might seem trivial at first glance. However, a deeper investigation reveals its importance in fundamental mathematical concepts, their applications in various fields, and its connection to more advanced mathematical ideas. This simple question provides a solid foundation for understanding arithmetic, laying the groundwork for more complex mathematical explorations. Its applications extend far beyond the classroom, permeating our everyday lives and playing a vital role in various scientific and technological advancements. By understanding this seemingly simple problem, we unlock a wealth of mathematical knowledge and appreciation for the power of basic arithmetic.
Latest Posts
Latest Posts
-
Honors Algebra 2 13 4 Sine And Cosine Graphs Worksheet
Jun 06, 2025
-
Determine The Stability Of Each Ecosystem
Jun 06, 2025
-
Use The Drop Down Menus To Complete Each Statement
Jun 06, 2025
-
Mr Oliver Orders His Groceries Online
Jun 06, 2025
-
What Is Another Activity Scott May Perform Within This Role
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about How Many 4s Are In 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.