How Many 5/16 Are In 1 7/8
Breaking News Today
Jun 04, 2025 · 4 min read
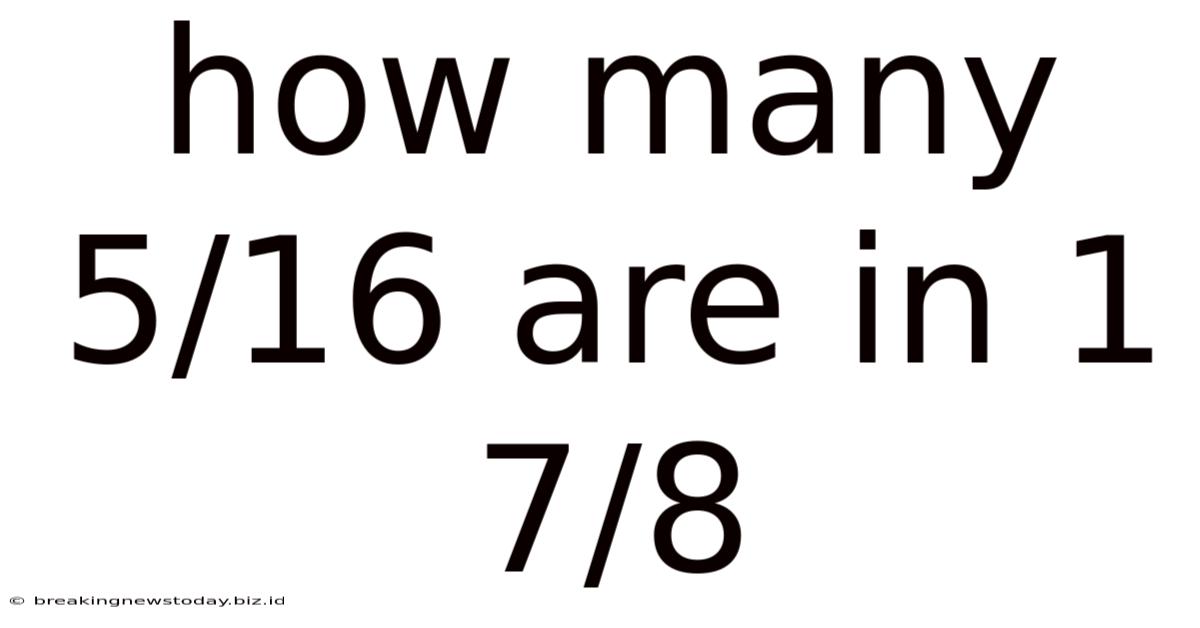
Table of Contents
How Many 5/16s Are in 1 7/8? A Deep Dive into Fraction Division
This seemingly simple question – "How many 5/16s are in 1 7/8?" – opens a door to a fascinating exploration of fraction manipulation and its practical applications. While a quick calculation might suffice for some, a deeper understanding of the underlying principles enhances problem-solving skills and builds a strong foundation in mathematics. This article will not only provide the solution but also delve into the 'why' and 'how', equipping you with a comprehensive understanding of fraction division.
Understanding the Problem: Deconstructing the Question
The core of the problem lies in determining how many times the fraction 5/16 fits into the mixed number 1 7/8. This translates directly into a division problem: (1 7/8) ÷ (5/16). Before diving into the calculation, let's address some key concepts:
What are Fractions?
Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many equal parts make up the whole.
Mixed Numbers vs. Improper Fractions
A mixed number (like 1 7/8) combines a whole number and a fraction. An improper fraction (like 15/8) has a numerator larger than its denominator. To perform calculations, it's often easier to convert mixed numbers into improper fractions.
Fraction Division: The Key Concept
Dividing fractions involves multiplying the first fraction by the reciprocal (inverse) of the second fraction. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 5/16 is 16/5.
Solving the Problem: Step-by-Step Guide
Let's solve the problem step-by-step:
-
Convert the Mixed Number to an Improper Fraction:
To convert 1 7/8 to an improper fraction, we multiply the whole number (1) by the denominator (8), add the numerator (7), and keep the same denominator. This gives us 15/8.
-
Rewrite the Problem:
Our problem now becomes (15/8) ÷ (5/16).
-
Find the Reciprocal:
The reciprocal of 5/16 is 16/5.
-
Multiply the Fractions:
Now we multiply 15/8 by 16/5: (15/8) x (16/5).
-
Simplify Before Multiplying (Optional but Recommended):
Notice that we can simplify before multiplying. 15 and 5 share a common factor of 5 (15 ÷ 5 = 3), and 16 and 8 share a common factor of 8 (16 ÷ 8 = 2). This simplifies the calculation significantly:
(3/1) x (2/1) = 6
-
The Answer:
Therefore, there are 6 5/16s in 1 7/8.
Visualizing the Solution: A Practical Approach
Imagine you have a pizza cut into 16 slices. 1 7/8 pizzas represent 15/16 + 16/16 = 31/16 of the pizza. A 5/16 slice of pizza is our reference unit.
Now, let’s determine how many 5/16 slices (our unit) are in 31/16 slices. We can visualize it by grouping the slices:
- Group 1: 5/16
- Group 2: 10/16
- Group 3: 15/16
- Group 4: 20/16
- Group 5: 25/16
- Group 6: 30/16
We are left with 1/16, which is less than our 5/16 unit. So, we definitively have 6 full groups of 5/16 in 31/16 which perfectly aligns with our calculation.
Extending the Knowledge: Real-World Applications
Understanding fraction division has numerous real-world applications, including:
-
Cooking and Baking: Scaling recipes up or down requires accurate fraction manipulation. If a recipe calls for 5/16 cup of flour, and you want to triple the recipe, you need to calculate 3 x (5/16).
-
Construction and Engineering: Precise measurements are critical in these fields. Calculating the number of smaller units within a larger unit (like determining how many 5/16-inch bolts fit within a 1 7/8-inch space) is vital.
-
Sewing and Quilting: Cutting fabric accurately involves working with fractions of inches. Determining how many smaller pieces can be cut from a larger piece requires mastering fraction division.
-
Data Analysis: In many fields, the data you’re analyzing involves fractions or percentages (which are essentially fractions).
Advanced Concepts and Further Exploration
This problem serves as a springboard for exploring more complex fraction-related concepts:
- Complex Fractions: These are fractions where either the numerator or the denominator (or both) contains a fraction.
- Decimal Conversions: Converting fractions to decimals can simplify certain calculations.
- Ratio and Proportion: Understanding ratios and proportions helps solve problems involving related fractions.
Mastering fraction division is a cornerstone of mathematical proficiency. The seemingly simple question of how many 5/16s are in 1 7/8 provides a valuable opportunity to reinforce fundamental concepts and build a stronger understanding of fractions. By understanding the principles behind the calculation and exploring its real-world applications, you'll not only be able to solve similar problems but also develop a broader mathematical literacy that will serve you well in various contexts. Remember to practice regularly, and don't be afraid to explore more challenging problems to further solidify your understanding.
Latest Posts
Latest Posts
-
Gina Wilson All Things Algebra Unit 2 Homework 7
Jun 06, 2025
-
A Popular Brand Of Cereal Puts A Card
Jun 06, 2025
-
Which Of The Following Accurately Describes The Term Hypothesis
Jun 06, 2025
-
The Evidence In This Passage Could Best Be Described As
Jun 06, 2025
-
Which Scientist And Atomic Model Are Correctly Matched
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about How Many 5/16 Are In 1 7/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.