How Many Hundreds Are In 200+10+6
Breaking News Today
Jun 06, 2025 · 5 min read
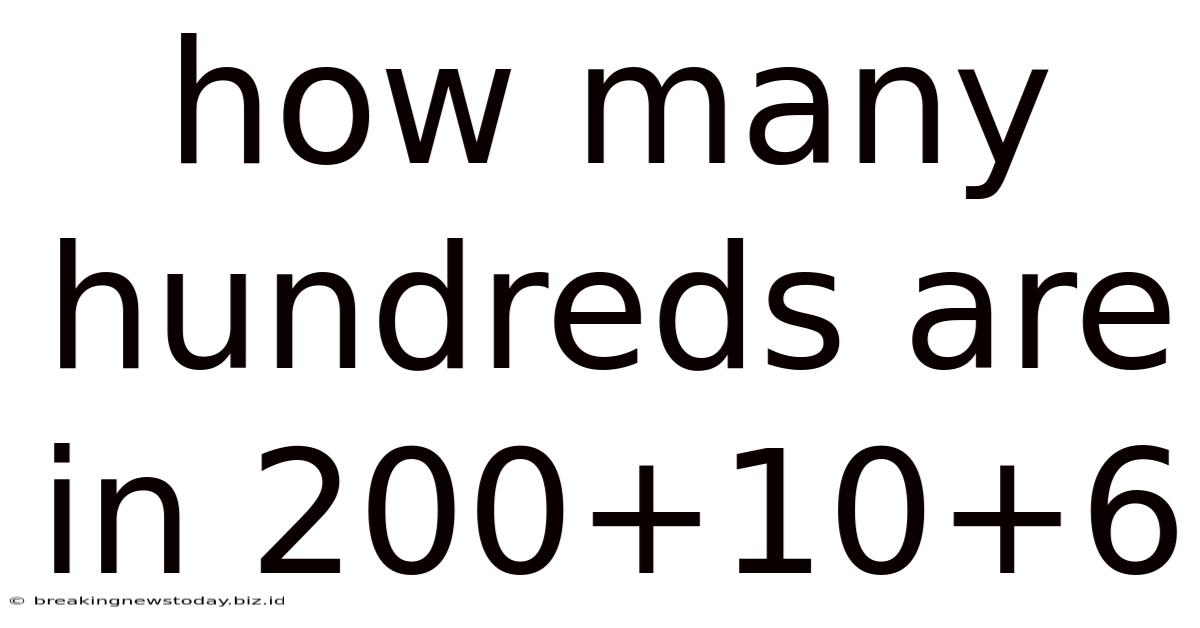
Table of Contents
Decoding the Hundreds: A Deep Dive into 200 + 10 + 6
This seemingly simple arithmetic problem, "How many hundreds are in 200 + 10 + 6?", opens a door to exploring fundamental mathematical concepts, problem-solving strategies, and even the fascinating world of number systems. While the immediate answer might seem obvious to many, a detailed examination reveals valuable insights applicable to various mathematical fields and beyond. This article will delve into the solution, explore related concepts, and offer practical applications of understanding this type of problem.
Understanding the Problem: Breaking Down the Components
The core of the problem lies in understanding the place value system. Our number system is based on powers of 10: ones, tens, hundreds, thousands, and so on. Each digit in a number holds a specific place value. In the expression 200 + 10 + 6, we have:
- 200: This represents two hundreds. The '2' occupies the hundreds place, signifying two groups of 100.
- 10: This represents one ten. The '1' is in the tens place, meaning one group of 10.
- 6: This represents six ones. The '6' is in the ones place.
Adding these together is straightforward addition: 200 + 10 + 6 = 216.
The Solution: Direct Calculation and Conceptual Understanding
The direct calculation leads us to the answer: 216. But the question isn't just about the sum; it's about identifying the number of hundreds within that sum.
Therefore, there are two hundreds in 200 + 10 + 6.
This seemingly simple answer provides a springboard for exploring more complex concepts:
Extending the Concept: Place Value and Number Representation
Understanding place value is crucial in mathematics. It forms the foundation for:
- Arithmetic Operations: Adding, subtracting, multiplying, and dividing all rely on a clear grasp of place value. Misunderstanding place value can lead to significant errors in calculations.
- Number Systems: Our decimal system (base-10) isn't the only one. Other systems, like binary (base-2) used in computers, or hexadecimal (base-16) used in color codes, utilize different place values.
- Larger Numbers: Extending this understanding allows us to easily work with numbers in the thousands, millions, billions, and beyond. The same principles apply, just with more places.
Practical Applications: Real-World Examples of Place Value
The concept of hundreds (and other place values) isn't confined to textbooks. It appears in numerous real-world scenarios:
- Finance: Managing money involves understanding hundreds, thousands, and even millions of dollars. Balancing budgets, calculating investments, and understanding debts all rely on accurate place value comprehension.
- Measurement: Units of measurement often involve place values. For example, 216 centimeters can be broken down into 2 meters (100 centimeters each) and 16 centimeters.
- Data Analysis: Understanding large datasets requires the ability to interpret numbers with varying place values, crucial for identifying trends and drawing meaningful conclusions.
- Engineering: Precise measurements and calculations are essential in engineering. Place value is vital in ensuring accuracy in blueprints, designs, and constructions.
Problem Solving Strategies: A Broader Perspective
The problem "How many hundreds are in 200 + 10 + 6?" might seem trivial, but it highlights valuable problem-solving approaches:
- Breaking Down Complex Problems: A larger problem is often easier to solve by breaking it down into smaller, manageable parts. This is exactly what we did by examining each component (200, 10, and 6) separately before combining them.
- Identifying Key Information: Understanding the question's intent is crucial. Here, the focus wasn't just on the sum but specifically on the number of hundreds within the sum.
- Visualizing the Problem: Using manipulatives (like blocks representing hundreds, tens, and ones) can help visualize the problem, particularly for younger learners. This provides a concrete representation of abstract concepts.
Beyond Hundreds: Exploring Thousands, Millions, and Beyond
Expanding this concept to larger numbers involves the same principles:
- Thousands: Consider the number 3,250. This contains three thousands (3000), two hundreds (200), five tens (50), and zero ones (0).
- Millions: A number like 1,575,000 contains one million (1,000,000), five hundred thousands (500,000), seven ten thousands (70,000), five thousands (5,000), and zero hundreds, tens, and ones.
- And beyond: The same principle extends to billions, trillions, and even larger numbers, simply adding more place values to the system.
Relating to Other Mathematical Concepts
Understanding hundreds and place value is intrinsically linked to other mathematical concepts:
- Number Theory: Exploring prime numbers, factors, and multiples often involves breaking down numbers into their constituent parts based on place value.
- Algebra: Manipulating variables and solving equations often requires understanding place value to properly represent and combine numerical expressions.
- Geometry: While less direct, understanding scales and measurements in geometry often relies on place value principles.
Conclusion: The Significance of a Simple Problem
The question "How many hundreds are in 200 + 10 + 6?" might appear simplistic, but it serves as a powerful entry point into a deeper understanding of fundamental mathematical concepts. By exploring place value, problem-solving strategies, and real-world applications, we unravel the significance of this seemingly basic arithmetic problem. Mastering this foundation enables more complex mathematical exploration and empowers individuals to tackle more challenging problems in various fields. The seemingly simple act of counting hundreds lays the groundwork for a much broader understanding of numbers and their applications in our world. This seemingly insignificant problem holds a vast amount of mathematical significance, underscoring the importance of a solid foundation in fundamental mathematical concepts. The ability to dissect and understand such problems is a cornerstone of mathematical literacy and problem-solving skills, skills applicable far beyond the classroom.
Latest Posts
Latest Posts
-
Tearing A Magazine Page Is An Example Of
Jun 07, 2025
-
Which Statement Describes A Property Of Covalent Compounds
Jun 07, 2025
-
Drivers Should Be Courteous And Allow At Least
Jun 07, 2025
-
Complete These Sentences About Medieval Plays
Jun 07, 2025
-
What Holds The Dampening Coil Springs In Place
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about How Many Hundreds Are In 200+10+6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.