How Many Tenths Are In 3/10
Breaking News Today
Jun 07, 2025 · 5 min read
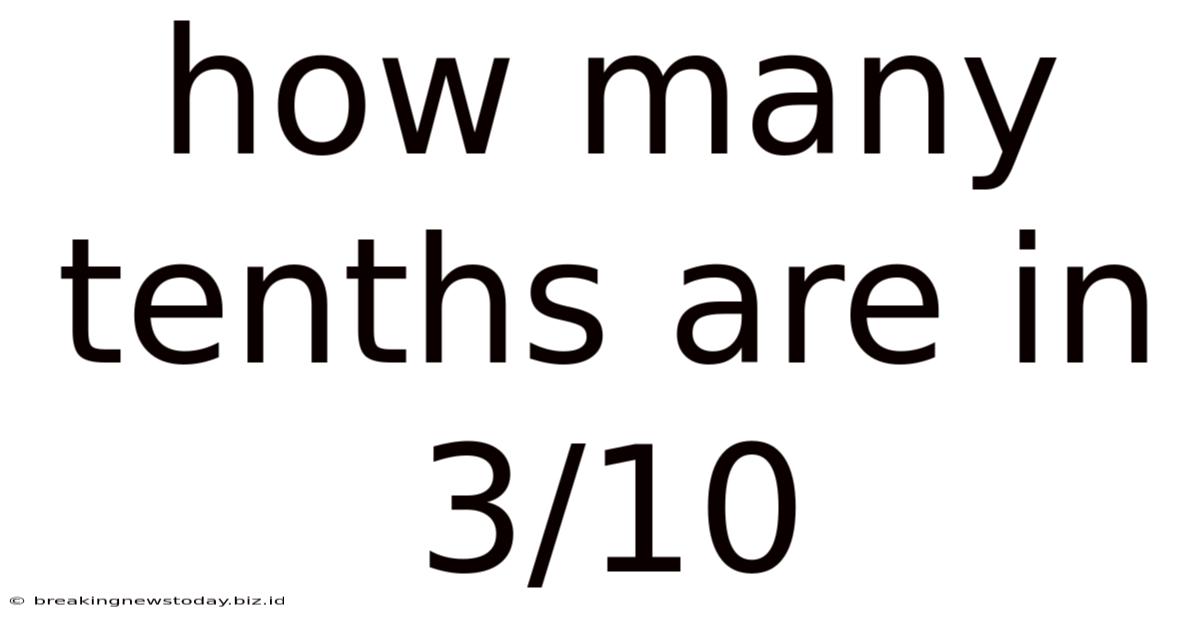
Table of Contents
How Many Tenths Are in 3/10? A Deep Dive into Fractions and Decimals
This seemingly simple question, "How many tenths are in 3/10?", opens a door to a fascinating exploration of fractions, decimals, and their interconnectedness. While the immediate answer might seem obvious, understanding the underlying concepts solidifies a crucial foundation in mathematics. This article will not only answer the question directly but also delve into the broader implications, providing a comprehensive understanding for students and anyone looking to refresh their math skills.
Understanding Fractions: A Building Block of Mathematics
Before tackling the main question, let's establish a firm grasp of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator specifies how many of those parts are being considered.
For instance, in the fraction 3/10, the denominator, 10, tells us the whole is divided into ten equal parts. The numerator, 3, indicates that we're considering three of those ten parts. This can be visualized easily: imagine a pizza cut into ten slices; 3/10 represents three slices of that pizza.
Key Concepts Related to Fractions:
-
Equivalent Fractions: These are fractions that represent the same value, even though they look different. For example, 1/2 is equivalent to 2/4, 3/6, 4/8, and so on. Understanding equivalent fractions is crucial for simplifying fractions and performing calculations.
-
Simplifying Fractions: This involves reducing a fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). For example, 6/12 can be simplified to 1/2 by dividing both 6 and 12 by 6.
-
Improper Fractions and Mixed Numbers: An improper fraction has a numerator that is greater than or equal to its denominator (e.g., 7/4). A mixed number combines a whole number and a fraction (e.g., 1 ¾). These are interchangeable representations of the same value.
Decimals: Another Way to Represent Parts of a Whole
Decimals provide an alternative way to express fractions. They use a base-ten system, with the decimal point separating the whole number part from the fractional part. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on.
For example, 0.1 represents one-tenth (1/10), 0.01 represents one-hundredth (1/100), and 0.001 represents one-thousandth (1/1000).
Connecting Fractions and Decimals: The Case of 3/10
Now, let's directly address the core question: How many tenths are in 3/10?
The fraction 3/10 literally means "three tenths." Therefore, the answer is three. There are three tenths in 3/10. This can also be expressed as the decimal 0.3.
Visualizing Tenths: Practical Examples
Understanding tenths is easier when visualized. Consider these scenarios:
-
Measuring Liquids: Imagine a measuring cup marked in tenths of a liter. 3/10 of a liter is simply 0.3 liters, or three marks on the measuring cup.
-
Money: If you have $1, and you divide it into ten equal parts (ten dimes), then 3/10 of a dollar is equivalent to 3 dimes, or $0.30.
-
Sharing Objects: If you have ten cookies, and you want to give 3/10 to a friend, that's three cookies.
Expanding the Concept: Beyond Tenths
While the initial question focused on tenths, let's broaden our perspective to understand how this applies to other fractions and decimals.
Converting Fractions to Decimals:
To convert any fraction to a decimal, you simply divide the numerator by the denominator. For example:
- 1/4 = 1 ÷ 4 = 0.25
- 2/5 = 2 ÷ 5 = 0.4
- 7/8 = 7 ÷ 8 = 0.875
Converting Decimals to Fractions:
To convert a decimal to a fraction, consider the place value of the last digit.
- 0.7 = 7/10 (seven tenths)
- 0.35 = 35/100 (thirty-five hundredths)
- 0.125 = 125/1000 (one hundred twenty-five thousandths)
These conversions are fundamental to understanding the relationship between fractions and decimals, allowing seamless transitions between the two forms.
Advanced Applications: Fractions in Real-World Scenarios
Fractions and decimals are not just abstract mathematical concepts; they find practical applications in numerous real-world situations:
-
Cooking and Baking: Recipes often involve fractional measurements (e.g., 1/2 cup of flour, 2/3 cup of sugar).
-
Construction and Engineering: Precise measurements are crucial in these fields, and fractions and decimals are used extensively to ensure accuracy.
-
Finance and Accounting: Calculations involving interest rates, percentages, and financial statements heavily rely on fractions and decimals.
-
Science: Many scientific calculations and measurements involve fractions and decimals, particularly in fields like chemistry and physics.
Troubleshooting Common Mistakes: Avoiding Pitfalls
When working with fractions and decimals, certain errors are common. Understanding these potential pitfalls can help prevent mistakes:
-
Incorrect simplification: Failing to simplify fractions to their lowest terms can lead to inaccurate calculations.
-
Decimal placement errors: Misplacing the decimal point can significantly alter the value of a number.
-
Improper conversion: Incorrectly converting between fractions and decimals can result in wrong answers.
-
Adding and subtracting fractions with different denominators: Fractions must have a common denominator before addition or subtraction can be performed.
By being aware of these potential pitfalls and practicing regularly, one can develop accuracy and confidence when working with fractions and decimals.
Conclusion: Mastering Fractions and Decimals
The seemingly simple question, "How many tenths are in 3/10?", has led us on a journey through the world of fractions and decimals. Understanding the relationship between these two representations of parts of a whole is fundamental to mathematical proficiency. From visualizing tenths using everyday examples to understanding advanced applications in various fields, this exploration has highlighted the significance and practicality of these core mathematical concepts. By mastering fractions and decimals, one builds a strong foundation for more complex mathematical endeavors and enhances problem-solving skills applicable to numerous real-world situations. Continuous practice and a focus on understanding the underlying principles are key to achieving fluency and confidence in working with these essential mathematical tools.
Latest Posts
Latest Posts
-
The Cost Of 10 Days At Healthy Gym Is
Jun 07, 2025
-
Which Passage Provides The More Effective Argument And Why
Jun 07, 2025
-
3 Letter Word That Means Regular Employment
Jun 07, 2025
-
Five Years Ago Benjamin Invested In Parchar Special Effects
Jun 07, 2025
-
1 3 Additional Practice Piecewise Defined Functions Answer Key
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about How Many Tenths Are In 3/10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.