How Many Terms Are In The Expression Shown 2n+5-3p+4q
Breaking News Today
Jun 08, 2025 · 4 min read
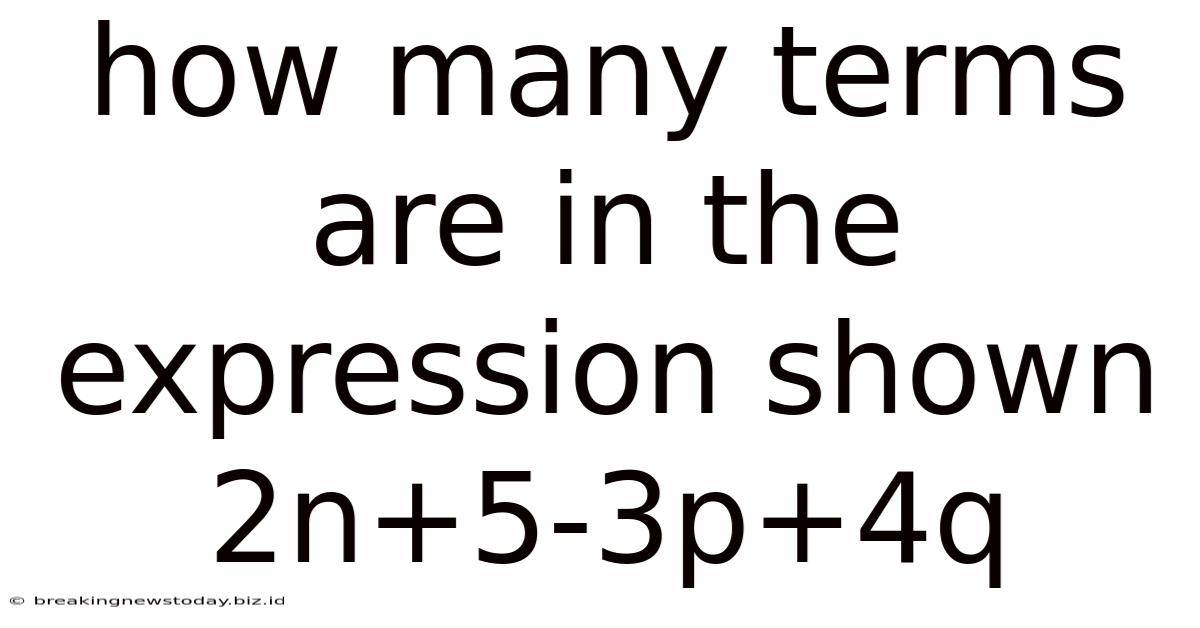
Table of Contents
How Many Terms Are in the Expression 2n + 5 - 3p + 4q? Understanding Algebraic Expressions
This seemingly simple question, "How many terms are in the expression 2n + 5 - 3p + 4q?", opens the door to a deeper understanding of algebraic expressions, a fundamental concept in mathematics. While the answer itself might seem immediately obvious, exploring the nuances of terms, variables, constants, and coefficients provides a solid foundation for more complex algebraic manipulations later on. Let's delve into this topic thoroughly.
What is an Algebraic Expression?
Before we tackle the specific expression, let's define what an algebraic expression is. An algebraic expression is a mathematical phrase that combines numbers, variables, and operations (like addition, subtraction, multiplication, and division). Unlike an equation (which has an equals sign), an expression doesn't equate to anything; it's simply a combination of mathematical components.
For example, 3x + 7, y² - 4, and (a + b)/c are all algebraic expressions. They contain variables (letters representing unknown values) and constants (fixed numerical values), connected by mathematical operations.
Identifying Terms in an Algebraic Expression
The key to answering our initial question lies in understanding what constitutes a term in an algebraic expression. A term is a single number, variable, or the product of numbers and variables. Crucially, terms are separated from each other by addition or subtraction signs. This is the primary rule to remember when counting terms.
Let's look at a few examples to solidify this concept:
Example 1: 3x + 7
This expression has two terms: 3x and 7. They are separated by the addition sign.
Example 2: y² - 4
This expression also has two terms: y² and -4. The subtraction sign separates the terms. Note that the negative sign is considered part of the term.
Example 3: 5ab + 2c - 8d
This expression contains three terms: 5ab, 2c, and -8d. The addition and subtraction signs clearly separate each term.
Example 4: x/y + 5z
This expression has two terms: x/y (x divided by y is considered a single term) and 5z.
Analyzing the Expression 2n + 5 - 3p + 4q
Now, let's return to our original expression: 2n + 5 - 3p + 4q. Applying the rules we've discussed, we can identify the terms:
- 2n: This is a term, a product of the constant 2 and the variable n.
- 5: This is a term; a constant term.
- -3p: This is a term; the product of -3 and the variable p. The negative sign is included as part of the term.
- 4q: This is a term; the product of 4 and the variable q.
Therefore, the expression 2n + 5 - 3p + 4q contains four terms.
Beyond Counting Terms: Understanding Components of Terms
While we've answered the main question, let's explore the different components within a term to gain a more comprehensive understanding of algebraic expressions.
Variables
Variables are represented by letters (like n, p, and q in our example) and represent unknown values or quantities. Variables can be raised to powers (exponents), as seen in expressions with terms like x² or y³.
Constants
Constants are fixed numerical values that do not change. In our expression, '5' is a constant term.
Coefficients
Coefficients are the numerical factors multiplying a variable in a term. In 2n, '2' is the coefficient of the variable 'n'. Similarly, in -3p, '-3' is the coefficient of 'p', and in 4q, '4' is the coefficient of 'q'.
Practical Applications and Further Exploration
Understanding terms in algebraic expressions is fundamental to various mathematical operations:
-
Simplifying Expressions: Combining like terms (terms with the same variables raised to the same powers) is a crucial step in simplifying complex expressions. For example,
3x + 5xsimplifies to8x. -
Solving Equations: Solving equations often involves manipulating algebraic expressions. Understanding terms helps in isolating variables and finding solutions.
-
Factoring Expressions: Factoring involves breaking down an expression into smaller components (factors), often using the properties of terms.
-
Polynomial Arithmetic: Polynomials are expressions with multiple terms involving variables with non-negative integer exponents. Understanding terms is critical for adding, subtracting, multiplying, and dividing polynomials.
Advanced Topics: Types of Algebraic Expressions
Let's briefly introduce some types of algebraic expressions, categorized by the number of terms:
- Monomial: An expression with only one term (e.g., 5x).
- Binomial: An expression with two terms (e.g., x + 5).
- Trinomial: An expression with three terms (e.g., x² + 2x + 1).
- Polynomial: A general term for expressions with one or more terms, including monomials, binomials, trinomials, and expressions with even more terms.
Conclusion: Mastering the Fundamentals
The seemingly simple question of how many terms are in 2n + 5 - 3p + 4q has served as a springboard for exploring the essential components of algebraic expressions. Understanding terms, variables, constants, and coefficients is crucial for success in algebra and beyond. By mastering these fundamental concepts, you lay a strong foundation for tackling more complex mathematical problems and advancing your understanding of higher-level algebraic concepts. Remember, the key is to carefully identify the addition and subtraction signs that separate the individual terms within the expression. Through consistent practice and a methodical approach, you will build confidence and proficiency in algebraic manipulation.
Latest Posts
Latest Posts
-
What Favor Does George Ask Of Candy
Jun 08, 2025
-
Como Se Escribe Medio Millon En Numeros
Jun 08, 2025
-
Which Of The Following Compounds Contains The Lead Ii Ion
Jun 08, 2025
-
This Circuit Could Be In Danger Of A What
Jun 08, 2025
-
What Percent Of 752 Is 25
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about How Many Terms Are In The Expression Shown 2n+5-3p+4q . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.