If 50 Percent Of X 66 Then X
Breaking News Today
Jun 05, 2025 · 5 min read
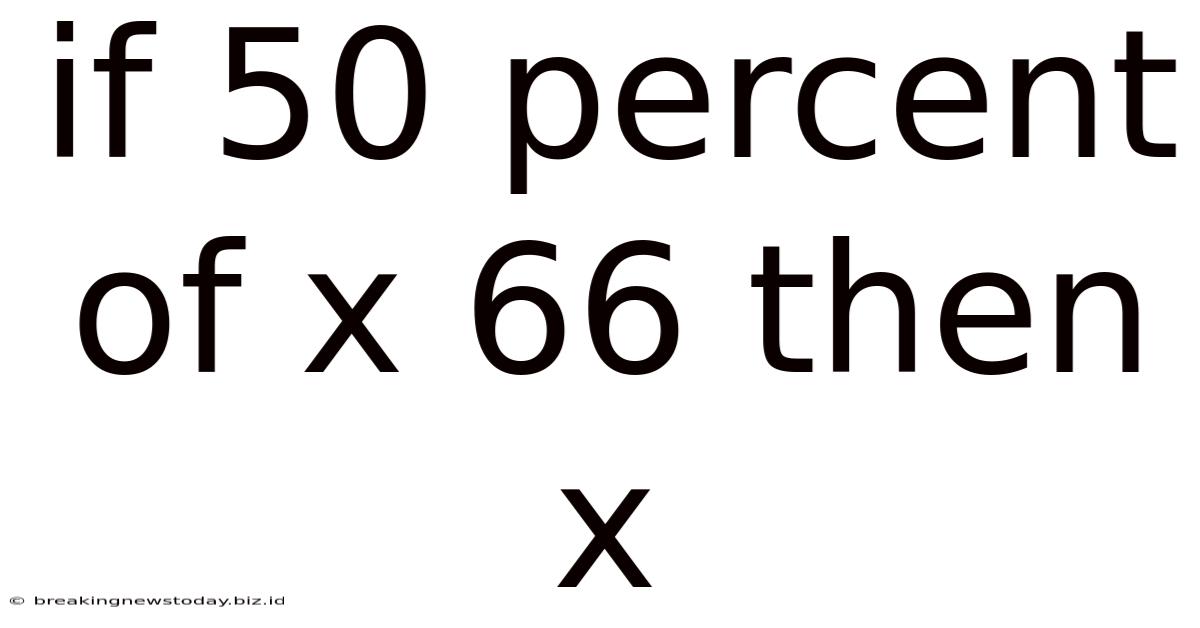
Table of Contents
If 50% of x = 66, Then x = ? A Comprehensive Guide to Solving Percentage Problems
This seemingly simple mathematical question, "If 50% of x = 66, then x = ?", underpins a crucial understanding of percentages and their application in various fields. While the solution itself is straightforward, delving deeper reveals the underlying principles and broader implications of percentage calculations. This article will not only solve the equation but also explore different approaches, address potential misconceptions, and provide practical examples to solidify your understanding.
Understanding Percentages: A Foundation
Before we tackle the problem directly, let's establish a solid understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100." For instance, 50% can be written as 50/100, which simplifies to 1/2 or 0.5.
This representation is key to solving percentage problems. We can express any percentage as a decimal or a fraction, allowing for flexible calculations.
Solving the Equation: If 50% of x = 66, Then x = ?
The problem states: 50% of x = 66. Let's translate this into a mathematical equation:
0.5 * x = 66
To solve for x, we need to isolate x on one side of the equation. We can do this by dividing both sides by 0.5:
x = 66 / 0.5
Therefore:
x = 132
Alternative Approaches to Solving the Problem
While the above method is the most straightforward, let's explore alternative approaches to demonstrate the versatility of percentage calculations:
Using Fractions:
We can rewrite 50% as the fraction 1/2. The equation then becomes:
(1/2) * x = 66
To solve for x, multiply both sides by 2:
x = 66 * 2
x = 132
Using Proportions:
We can set up a proportion to solve this problem. A proportion is an equation stating that two ratios are equal. In this case, we can write:
50/100 = 66/x
Cross-multiplying gives:
50x = 6600
Dividing both sides by 50:
x = 132
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of life, from everyday finances to complex scientific analyses. Here are some examples:
Finance:
-
Calculating discounts: A common application is calculating discounts on sales. If an item is 20% off, and its original price is $100, the discount is 0.2 * $100 = $20, and the final price is $80.
-
Calculating interest: Interest rates on loans and investments are expressed as percentages. Understanding percentage calculations is essential for managing finances effectively.
-
Analyzing financial statements: Financial statements, such as balance sheets and income statements, use percentages extensively to present data clearly and concisely.
-
Tax calculations: Sales taxes, income taxes, and other taxes are often calculated as a percentage of the taxable amount.
Science and Statistics:
-
Data analysis: Percentages are frequently used to present and analyze data, allowing for comparisons and trends identification.
-
Probability and statistics: Percentages are fundamental to probability and statistics, particularly when expressing likelihoods and distributions.
Everyday Life:
-
Calculating tips: Calculating a tip in a restaurant often involves using percentages. A 15% tip on a $50 bill is 0.15 * $50 = $7.50.
-
Understanding survey results: Survey results are often presented using percentages to summarize responses from a large population.
-
Cooking and baking: Recipes often specify ingredients as percentages of the total weight or volume, allowing for flexible scaling.
Common Misconceptions about Percentages
While seemingly simple, percentages can be a source of confusion. Let's address some common misconceptions:
-
Adding percentages directly: You cannot simply add percentages directly unless they are of the same base. For instance, a 10% increase followed by a 10% decrease does not result in a net change of 0%. The final result is dependent on the initial value.
-
Confusing percentage change with percentage points: A percentage change refers to the relative change, whereas percentage points refer to the absolute difference. A change from 10% to 20% is a 10 percentage point increase, but a 100% percentage increase.
-
Incorrect use of percentages in comparisons: Comparing percentages without considering the base values can lead to misleading conclusions.
Advanced Percentage Problems and Techniques
While the initial problem was relatively straightforward, more complex percentage problems may involve multiple steps or require a deeper understanding of algebraic manipulations.
Compound Interest:
Compound interest calculations involve accruing interest on both the principal amount and accumulated interest. These calculations require a more advanced understanding of exponential growth.
Percentage Increase/Decrease:
Calculating the percentage increase or decrease between two values involves finding the difference, dividing it by the original value, and then multiplying by 100.
Percentage Points vs. Percentage Change:
Understanding the subtle distinction between percentage points and percentage change is crucial for accurately interpreting data.
Percentage of a Percentage:
Problems involving finding a percentage of a percentage necessitate careful attention to order of operations and proper conversion to decimal form.
Conclusion
Solving the problem "If 50% of x = 66, then x = ?" is a gateway to understanding a broader spectrum of mathematical applications involving percentages. Mastering percentage calculations is not merely about solving equations; it’s about developing a robust analytical skill applicable to numerous fields. From daily budgeting to interpreting complex datasets, the ability to work confidently with percentages is an invaluable asset. By understanding the underlying principles, addressing common misconceptions, and practicing diverse problem-solving techniques, you can unlock the full potential of percentage calculations and apply them effectively in your personal and professional life. This article serves as a stepping stone, encouraging further exploration and deeper understanding of this fundamental mathematical concept. Remember, practice makes perfect, so continue to challenge yourself with increasingly complex percentage problems to refine your skills and become a proficient percentage master!
Latest Posts
Latest Posts
-
The Following Image Illustrates Which Design Principle
Jun 07, 2025
-
A Pound Of Popcorn Is Popped For A Class Party
Jun 07, 2025
-
Study The Data Set Shown Then Answer The Questions Below
Jun 07, 2025
-
A Ball Of Unknown Mass M Is Tossed Straight Up
Jun 07, 2025
-
Which Details Directly Characterize Dr Lanyon Check All That Apply
Jun 07, 2025
Related Post
Thank you for visiting our website which covers about If 50 Percent Of X 66 Then X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.